Current Density

Current density refers to the amount of electric current flowing through a specific area of a conductor. It is an important concept in understanding how electricity moves within materials. In real-life applications, current density is crucial for designing safe and efficient electrical systems, such as ensuring that wires do not overheat. It also plays a significant role in technologies like electroplating and battery design, where controlling the current flow is essential for optimal performance. For students preparing for exams like JEE or NEET, understanding current density helps in solving complex electrical problems effectively.

What is Current Density?

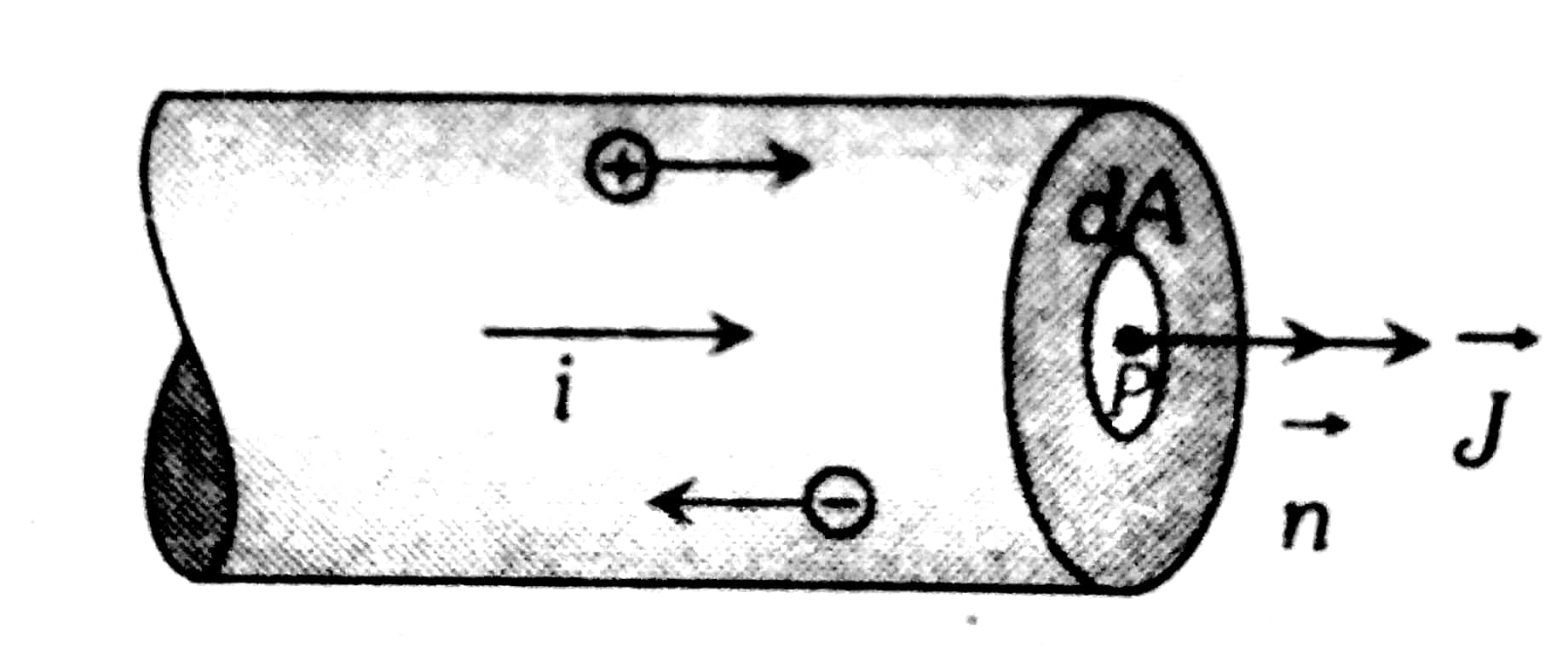
The amount of electric current flowing per unit cross-sectional area of a material. It is a vector quantity.

If a current of $\Delta i$ flows through an area $\Delta A$ the average current density $\bar{j}=\frac{\Delta i}{\Delta A}$ in the direction of the current.

At point P :

$j=\lim _{\Delta A \rightarrow 0} \frac{\Delta i}{\Delta A} \text { in the direction of the current }$

If current not Perpendicular to Area

\begin{aligned}
& J_{a v}=\frac{d i}{d A \cos \theta} \\
& d i=J d A \cos \theta=\vec{J} \cdot d \vec{A}
\end{aligned}

$\theta$ is the angle between the normal area and the direction of the current
If the current density $\vec{J}$ is uniform for a normal cross-section $\vec{A}$ then,

$
i=\int \vec{J} \cdot d \vec{A}
$

• The unit of current density is $A \mathrm{mp} / \mathrm{m}^2$
• The dimension of current density is $\left[L^{-2} A\right]$

Recommended Topic Video

Solved Examples Based on Current Density

Example 1: A wire has a non-uniform cross-section as shown. A steady current is flowing through it. Then the current density

1) is constant throughout the wire

2) decreases from A to B

3) increases from A to B

4) varies randomly

Solution:

The current density is J= I/A

I is constant, and Area increases as we move from A to B.

Hence Current density J will decrease as we move from A to B.

Hence, the answer is option (2).

Example 2: Current density through a cylindrical wire of radius R varies as j=kr, where k is a constant and r is its distance from the axis of the cylinder. Then the total current passing through the wire is:

1) $\pi R^2 k$
2) $\pi R^3 k$
3) $\frac{2 \pi R^3 k}{3}$
4) $\frac{\pi R^3 k}{3}$

Solution:

If the current density is not uniform -
$
I=\int \vec{J} \cdot d \vec{A}
$

wherein

The direction for $J$ is usually in the direction of the $\mathrm{E}$-field.
$
I=\int_0^R \vec{J} \cdot d \vec{A}=\int_0^R k r(2 \pi r d r)=\frac{2 \pi R^3 k}{3}
$

Hence, the answer is the option (3).

Example 3: While calculating current passing through a wire which area is taken?

1) Area perpendicular to the flow of current

2) Area parallel to the flow of current

3) Any area

4) Maximum area

Solution:

If current not Perpendicular to Area

$\begin{aligned}
& J_{a v}=\frac{d i}{d A \cos \theta} \\
& d i=J d A \cos \theta=\vec{J} \cdot d \vec{A}
\end{aligned}$

wherein

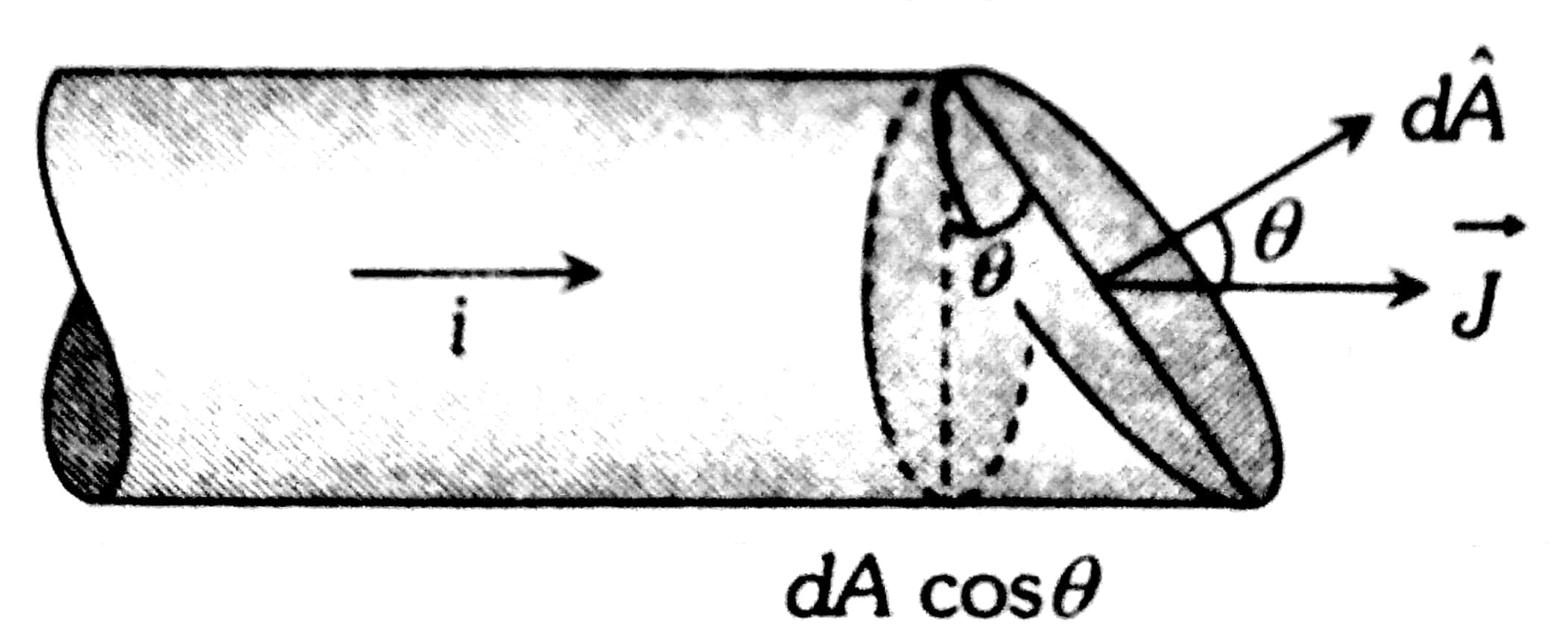
We always take that area which is perpendicular to the current flow.

Hence, the answer is option (1).

Example 4: The current density in a cylindrical wire of radius 4mm is $4 \times 10^6 \mathrm{Am}^{-2}$. The current through the outer portion of the wire between radial distances $\frac{R}{2}$ and R is ____________$\pi \mathrm{A}$.

1) 48

2) 49

3) 50

4) 51

Solution:

Current Density

$\begin{aligned}
& \mathrm{J}=\frac{\mathrm{I}}{\mathrm{A}} \\
& \mathrm{I}=\mathrm{JA}
\end{aligned}$

$\begin{aligned}
\mathrm{I} & =\mathrm{J} \times\left[\pi \mathrm{R}^2-\pi\left(\frac{\mathrm{R}^2}{2}\right)^2\right] \\
& =\mathrm{J} \times\left(\pi \mathrm{R}^2-\frac{\pi \mathrm{R}^2}{4}\right) \\
& =\mathrm{J} \times \frac{3 \pi \mathrm{R}^2}{4} \\
& =4 \times 10^6 \times \frac{3 \pi}{4} \times 16 \times 10^{-6} \\
& =48 \pi \mathrm{A}
\end{aligned}$

Hence the answer is option (1).

Example 5: The current density in a cylindrical wire of radius $\mathrm{r}=4.0 \mathrm{~mm} \text { is } 1.0 \times 10^6 \mathrm{~A} / \mathrm{m}^2$. The current through the outer portion of the wire between radial distances $\frac{r}{2}$ and r is $\mathrm{x} \pi \mathrm{A} \text {; where } \mathrm{x} \text { is }$ ______.

1) 12

2) 13

3) 14

4) 15

Solution:

$\mathrm{J}=\frac{\mathrm{I}}{\mathrm{A}}$

$\begin{aligned}
\mathrm{I} & =\left[\mathrm{J} \times\left[\pi \mathrm{r}^2-\frac{\pi \mathrm{r}^2}{4}\right]\right]=\mathrm{J} \times \frac{3 \pi \mathrm{r}^2}{4} \\
& =1 \times 10^6 \times \frac{3}{4} \times \pi \times 16 \times 10^{-6} \\
& =12 \pi
\end{aligned}$

Hence, the answer is option (1).

Summary

When electric current flows through a conductor, the flow of electrons per unit area in an electric circuit is referred to as current density. Amperes are used to measure the current density per square meter in this case. It should be noted that high current density results in extreme heating and damages that can discontinue the normal operation of conductors. It is necessary to understand and apply appropriate levels of this amount so as to avoid accidents due to electrical faults or poor operational methods used.