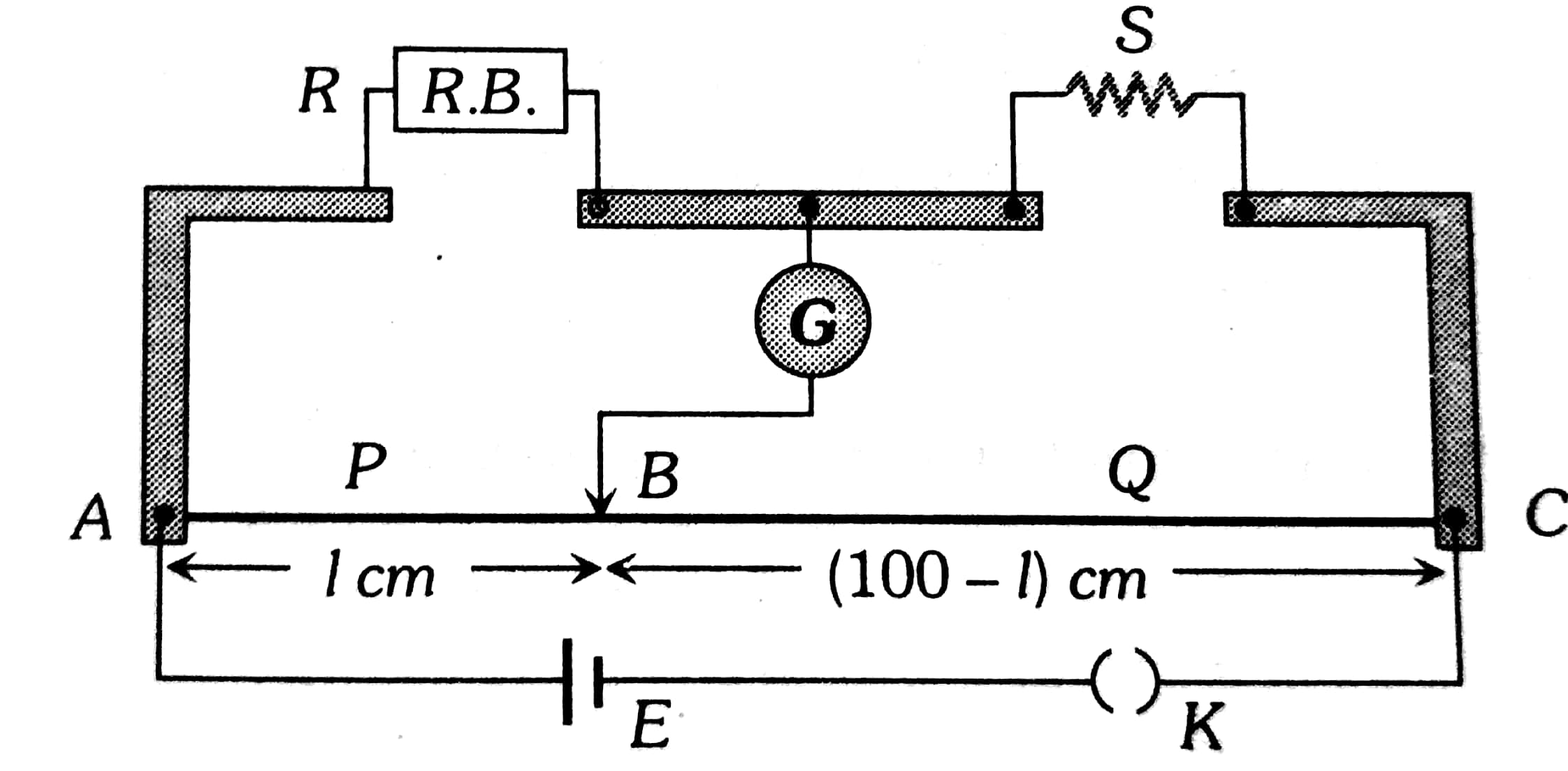
Meter Bridge
The Meter Bridge, which is probably one of the most interesting and practical of all experiments in the science of physics, lends itself to a vivid understanding of the resistance phenomenon as it works in a circuit. The Meter Bridge experiment is widely used to demonstrate Ohm's Law and to understand the Wheatstone Bridge setup and hence forms a very important element in the education of students. From this experiment, one can obtain measurements of unknown resistances toward a better understanding of how balance occurs in electrical circuits. Preparing for an examination or just wondering how electrical measurements work? Well, a Meter Bridge will give you an easy yet powerful tool to familiarise yourself with resistance and circuits.
- What is the Meter Bridge?
- What is the Principle of the Meter Bridge and Potentiometer?
- Meter Bridge Experiment
- Meter Bridge Questions and Answers
What is the Meter Bridge?
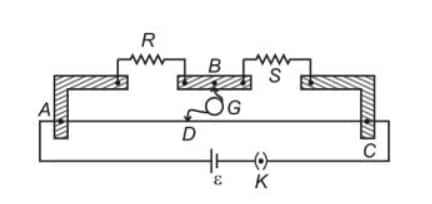
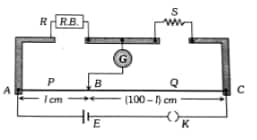
A Meter Bridge is a device used to measure unknown resistances based on the principle of Wheatstone's Bridge. It consists of a 1-meter-long wire mounted on a bridge with known resistors and unknown resistors connected in the circuit. The bridge can be balanced, and the resistance of the unknown resistor is calculated from the length ratio of the wire on either side of the jockey.
Meter Bridge Diagram
What is Another Name for a Metre Bridge?
Another name for the Meter Bridge is the Slide Bridge. In some instances, it is also referred to as a Wheatstone Bridge with respect to its principle of working, because it works on the Wheatstone Bridge method to measure unknown resistances.
What is the Principle of the Meter Bridge and Potentiometer?
The principle of the meter bridge and potentiometer is given below.
Principle of the Meter Bridge
The meter bridge works on the principle of a Wheatstone bridge. It states that when the bridge is balanced, the ratio of the resistances in the two arms of the bridge is equal to the ratio of the lengths of the wire on either side of the jockey.
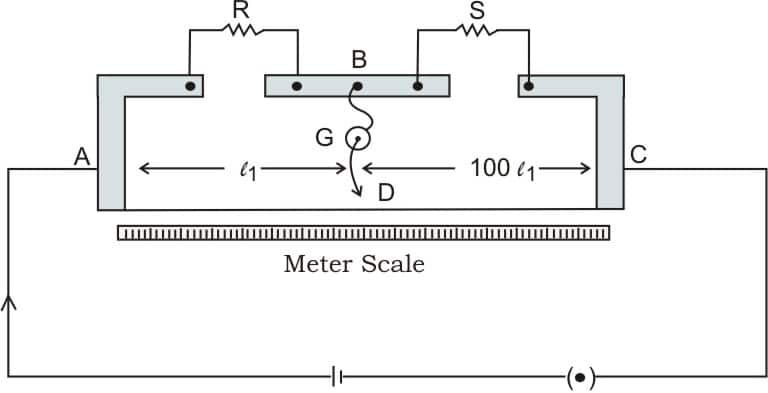
That is mathematically: $\frac{R_1}{R_2}=\frac{l_1}{l_2}$
Where:
- $\quad R_1$ and $R_2$ are the resistances in the two arms of the bridge.
- $l_1$ and $l_2$ are the lengths of the wire on either side of the jockey.
Principle of the Potentiometer
The voltage drop across a section of an element of a uniform wire is proportional to the length of that section. Thus, a potential difference-measuring instrument called the potentiometer can be used without drawing current. The concept itself is simple: for constant current, the voltage drop is proportional to the length of the wire:
$
V=k \times l
$
Where:
$V$ is the potential difference, $k$ is a constant (determined by the current and the resistance of the wire), and $l$ is the length of the wire.
Recommended Topic Video
Meter Bridge Experiment
Meter Bridge experiment provides a means of measuring unknown resistances by the construction of a Wheatstone Bridge. It consists of a 1-meter wire, which is held horizontally on a wooden or metal base, attached to both arms of the bridge with known resistors. The null point is thus achieved when the galvanometer reads zero, which means that the bridge is in a state of equilibrium.
Objective: Measurement of unknown resistance with the use of the Meter Bridge.
Apparatus:
- Meter Bridge (1-meter-long wire)
- Galvanometer
- Jockey
- Known resistor
- Unknown resistor$ R_1$ and $ R_2$
- Battery and key
- Connecting wires
Principle: The Meter Bridge is based on the principle of the Wheatstone Bridge, which states that when the bridge is in balance:
$\frac{R_1}{R_2}=\frac{l_1}{l_2}$
Procedure:
1. Setup: Connect the known resistor $R_1$ and unknown resistor $R_2$ to the meter bridge. Attach the galvanometer and jockey to the bridge.
2. Balance the Bridge: Close the key to allow current to flow. Slide the jockey along the wire until the galvanometer shows zero deflection, indicating the balance point.
3. Calculate the Unknown Resistance: Using the formula $\frac{R_1}{R_2}=\frac{l_1}{l_2}$, calculate the unknown resistance $R_2$.
Formula:
$
R_2=R_1 \times \frac{l_2}{l_1}
$
Where:
- $l_1$ and $l_2$ are the lengths measured on either side of the jockey.
Applications:
- Measurement of unknown resistances.
- Verification of Ohm's Law.
- Determining the specific resistance of a material.
Related Links-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Meter Bridge Questions and Answers
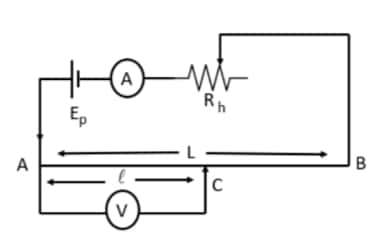
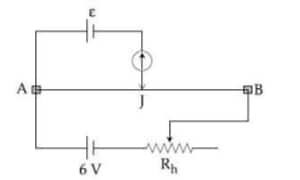
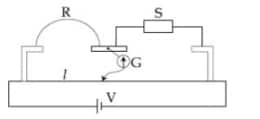
Example 1:
The resistance of meter bridge AB in a given figure is $4 \Omega$. With the cell of emf $\varepsilon=0.5 \mathrm{~V}$ and rheostat resistance $\mathrm{R}_{\mathrm{h}}=2 \Omega$ the null point is obtained at some point $\mathrm{J}$. When the cell is replaced by another one of emf $\varepsilon=\varepsilon_2$ the same null point $\mathrm{J}$ is found for $R_h=6 \Omega$. The emf $\varepsilon_2$ (in $\mathrm{V}$ ) is:
1) 0.3
2) 0.4
3) 0.6
4) 0.5
Solution:
Meter bridge
$
\frac{P}{Q}=\frac{R}{S} \Rightarrow S=\frac{(100-l)}{l} R
$
wherein
$
\begin{aligned}
& A B=l \\
& B C=(100-l)
\end{aligned}
$
For the question
When $R_h=2 \Omega$
$
\frac{d V}{d L}=\left(\frac{6}{4+2}\right) \times \frac{4}{L}
$
where $L=100 \mathrm{~cm}$
Let the null point be at $l \mathrm{~cm}$Let the null point be at l cm
$
\varepsilon_1=0.5 \mathrm{~V}=\left(\frac{6}{2+4}\right) \frac{4}{L} l ...... (1)
$
for $R_h=6 \Omega$
$
\varepsilon_2=\left(\frac{6}{4+6}\right) \frac{4}{L} \times l \ldots \ldots \ldots(2)
$
From equation (1) and (2)
$
\begin{aligned}
& \frac{0.5}{\varepsilon_2}=\frac{10}{6} \\
& \Rightarrow \varepsilon_2=0.3
\end{aligned}
$
Hence, the answer is option (1).
Example 2:
In a meter bridge experiment, S is the standard resistance, and R is the resistance wire. It is found that the balancing length is l=25 cm. If R is replaced by a wire of half length and half diameter that of R of the same material, then the balancing distance $l^{\prime}$ (in cm) will now be _____.
1) 400
2) 40
3) 20
4) 30
Solution:
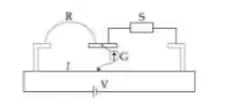
$\begin{aligned}
& \frac{X}{R}=\frac{75}{25}=3 \\
& R=\frac{P^l}{A}=\frac{4 P^l}{\pi d^2} \\
& R^{\prime}=\frac{4 \rho\left(\frac{l}{2}\right)}{\pi\left(\frac{d}{2}\right)^2}=2 R \\
& \text { then, } \frac{x}{R^{\prime}}=\frac{X}{2 R}=\frac{3}{2} \\
& l=40.00 \mathrm{~cm}
\end{aligned}$
Hence, the answer is option (2).
Example 3:
Consider a 72cm long AB as shown in the figure. The galvanometer jockey is placed at P on AB at a distance of x cm from A. The galvanometer shows zero deflection.
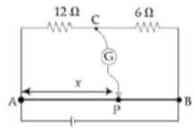
The value of x, to the nearest integer, is ____
1) 48
2) 96
3) 24
4) 72
Solution:
In Balanced conditions
$
\begin{aligned}
& \frac{12}{6}=\frac{x}{72-x} \\
& x=48 \mathrm{~cm}
\end{aligned}
$
Hence, the answer is option (1).
Example 4:
On interchanging the resistances, the balance point of a meter bridge shifts to the left by 10 cm. The resistance of their series combination is 1 kΩ. How much was the resistance (in $\Omega$ ) on the left slot before interchanging the resistances?
1) 550
2) 990
3) 505
4) 910
Solution:
Meter bridge
To find the resistance of a given wire using a meter bridge and hence determine the specific resistance of its materials
wherein
Let's say resistances are R and 1000-R
Case 1: $\frac{R}{l}=\frac{1000-R}{100-l} \quad$ .... (1)
Case II: $\frac{1000-R}{l-10}=\frac{R}{110-l}$ .................(2
Multiply both equations
$
\begin{aligned}
& \frac{R(1000-R)}{l(l-10)}=\frac{R(1000-R)}{(100-l)(110-l)} \Rightarrow l^2-10 l=11000+l^2-210 l \\
& \Rightarrow 200 l=11000 \\
& \text { or } l=55 \mathrm{~cm} \\
& \Rightarrow \frac{R}{55}=\frac{1000-R}{45}
\end{aligned}
$
or $45 R=55000-55 R$
or $R=550 \Omega$
Hence, the answer is option (1).
Example 5:
In the shown arrangement of the experiment of a meter bridge, if AC corresponding to the null deflection of the galvanometer is x, what would be its value if the radius of the wire AB is doubled?
1) $x$
2) $\frac{x}{4}$
3) $4 x$
4) $2 x$
Solution:
At null point
$\frac{R_1}{R_2}=\frac{R_3}{R_4}=\frac{x}{100-x}$
if the radius of the wire is doubled then the resistance of AC will change and the resistance of CB will also change.
But since $\frac{R_1}{R_2}$ does not change so $\frac{R_3}{R_4}$ should also not change at a null point. Therefore point C does not change.
Hence, the answer is option (1).
A slide wire bridge, also known as a meter bridge, is an instrument to compare an unknown resistance with a known level of resistance. Its principle is based on the theory of the Wheatstone Bridge, consisting of a one-meter-long uniform cross-section wire stretched on a wooden board and calibrated. On moving the contact point on this metallic conductor, one gets a balanced point for which there is no deflection on the Galvanometer.
Also Read-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Frequently Asked Questions (FAQs)
A meter bridge is an electrical device used to measure unknown resistances. It works on the principle of Wheatstone bridge, where four resistors are arranged in a diamond shape. One of these resistors is the unknown resistance, while the other three are known. By adjusting a sliding contact along a wire of uniform resistance, the bridge is balanced when no current flows through the galvanometer. This balance point allows us to calculate the unknown resistance.
The meter bridge wire is typically made of constantan because it has a high resistivity and a low temperature coefficient of resistance. This means its resistance remains relatively constant over a range of temperatures, ensuring accurate measurements regardless of slight temperature fluctuations during the experiment.
In a balanced meter bridge, the ratio of the lengths of the wire on either side of the galvanometer is equal to the ratio of the resistances in the corresponding arms of the bridge. This relationship is expressed as L1/L2 = R1/R2, where L1 and L2 are the lengths of the wire, and R1 and R2 are the resistances in the respective arms.
The null point in a meter bridge experiment is the position of the sliding contact where the galvanometer shows zero deflection. This point indicates that the bridge is balanced, meaning no current flows through the galvanometer. The null point is crucial for determining the unknown resistance, as it represents the point of equal potential between the two arms of the bridge.
The sensitivity of a meter bridge is highest at the center and decreases towards the ends. This is because small changes in the position of the sliding contact near the center result in larger changes in the resistance ratio, making it easier to detect the null point. Near the ends, larger movements are required to produce the same change in resistance ratio, reducing sensitivity.
Interchanging the positions of known and unknown resistances helps to eliminate errors due to any non-uniformity in the resistance of the meter bridge wire. By taking the average of the two measurements, we can obtain a more accurate result, as any systematic errors due to wire irregularities are minimized.
The end resistance of connecting wires can introduce errors in meter bridge measurements. These resistances add to the resistance being measured, leading to inaccurate results. To minimize this effect, it's important to use thick, short connecting wires and ensure good contact at all connection points.
The jockey in a meter bridge setup serves as a sliding contact that can be moved along the meter bridge wire. It allows for precise adjustment of the contact point, enabling the experimenter to find the exact null point where the galvanometer shows zero deflection. The jockey's ability to make and break contact quickly also helps prevent heating of the wire due to prolonged current flow.
The choice of galvanometer affects the accuracy of meter bridge measurements through its sensitivity. A more sensitive galvanometer can detect smaller current imbalances, allowing for a more precise determination of the null point. However, an overly sensitive galvanometer might make it difficult to achieve a stable null reading. The ideal galvanometer should have sufficient sensitivity to detect small current changes without being too easily disturbed by minor fluctuations.
Avoiding parallax error is crucial when reading the meter bridge scale to ensure accurate measurements. Parallax error occurs when the observer's line of sight is not perpendicular to the scale, leading to an incorrect reading of the jockey's position. To minimize this error, the observer should ensure their eye is directly above the jockey when taking readings, using the reflection of their eye in the mirror strip often provided alongside the scale.
The thickness of the meter bridge wire affects its functionality by influencing its resistance per unit length. A thicker wire has lower resistance per unit length, which can reduce the overall sensitivity of the bridge. However, it also allows for higher current capacity and better heat dissipation. The ideal wire thickness balances these factors to provide good sensitivity while avoiding excessive heating or voltage drops.
Temperature changes can affect meter bridge measurements by altering the resistance of the wire and other components. As temperature increases, the resistance of most metals increases, which can lead to inaccurate readings. This is why constantan is often used for the bridge wire, as its resistance changes very little with temperature. To minimize temperature effects, it's important to conduct experiments in a temperature-controlled environment and allow the apparatus to reach thermal equilibrium before taking measurements.
The concept of potential gradient is fundamental to the meter bridge's operation. Along the uniform resistance wire, there is a linear potential gradient. When the bridge is balanced, the potential at the galvanometer connection point is the same on both sides of the bridge. This equality of potentials at the balance point is what allows us to relate the lengths of wire segments to the resistances in the bridge arms, forming the basis for resistance measurement.
Using a low-voltage power source in a meter bridge setup is important for several reasons. Firstly, it helps prevent excessive current flow, which could heat the wire and change its resistance, leading to inaccurate measurements. Secondly, it ensures the safety of the experimenter and the equipment. Lastly, a low voltage helps maintain the linearity of the potential gradient along the wire, which is crucial for the accuracy of the measurements.
The resistance per unit length of the meter bridge wire directly affects measurement accuracy. Ideally, this resistance should be uniform along the entire length of the wire. Any variations can lead to non-linear potential gradients, causing errors in the resistance ratios calculated from length measurements. A wire with consistent resistance per unit length ensures that the relationship between wire length and resistance remains linear, maintaining the accuracy of the bridge measurements.
Meter bridges have limitations when measuring very high or very low resistances. For very high resistances, the current in the circuit becomes extremely small, making it difficult to detect the null point accurately. For very low resistances, the resistance of the connecting wires and contact points becomes significant compared to the resistance being measured, introducing large errors. Additionally, the finite resistance of the meter bridge wire itself can limit accuracy when measuring resistances comparable to or less than its own resistance.
The meter bridge and potentiometer both operate on similar principles of potential division. In a meter bridge, we compare potential drops across different resistances to find an unknown resistance. Similarly, a potentiometer compares potential drops to measure unknown voltages or EMFs. Both devices use a wire of uniform resistance to create a known potential gradient, and both rely on finding a point of zero potential difference (null point) to make measurements.
Keeping the meter bridge wire taut and straight is crucial for accurate measurements. A loose or curved wire can lead to inconsistent contact with the jockey, causing fluctuations in readings. Moreover, a straight wire ensures that the length measured along the scale accurately corresponds to the resistance of that segment. Any sagging or bending in the wire could lead to discrepancies between the measured length and the actual resistance, introducing errors in the calculations.
The internal resistance of the battery can affect meter bridge measurements by altering the current distribution in the circuit. If the internal resistance is significant, it can cause a voltage drop that varies with the position of the jockey, leading to non-linear potential gradients along the wire. This can result in inaccurate resistance measurements. To minimize this effect, it's advisable to use a battery with low internal resistance or to account for it in the circuit analysis if it's significant.
Kirchhoff's laws play a crucial role in understanding meter bridge operation. Kirchhoff's Current Law (KCL) ensures that the current entering any junction in the bridge equals the current leaving it. Kirchhoff's Voltage Law (KVL) guarantees that the sum of potential differences around any closed loop in the circuit is zero. These laws explain why, at the balance point, no current flows through the galvanometer – the potential difference across it is zero because the voltage drops in both arms of the bridge are equal.
Contact resistance between the jockey and the wire can introduce errors in meter bridge measurements. This resistance, if significant, adds to the resistance being measured and can vary with the pressure applied to the jockey. To minimize its effect, the jockey should be designed to make firm, consistent contact with the wire. Some setups use a knife-edge contact to reduce the contact area and thus the contact resistance. Regular cleaning of the wire and jockey also helps maintain good electrical contact.
Avoiding kinks or bends in the connecting wires of a meter bridge setup is important because such deformities can increase the resistance of the wires. This additional resistance can introduce errors in the measurements, especially when measuring low resistances. Straight, taut connecting wires ensure that their resistance remains minimal and consistent, contributing to more accurate results.
The concept of resistivity is crucial in understanding the meter bridge wire's behavior. The resistivity of the wire material determines its resistance per unit length, which should be uniform for accurate measurements. The resistance of a segment of the wire is given by R = ρL/A, where ρ is the resistivity, L is the length, and A is the cross-sectional area. Uniform resistivity ensures that the resistance is directly proportional to the length, which is fundamental to the meter bridge's operation.
A standard resistance box is significant in meter bridge experiments as it provides known, accurate resistances for comparison. These calibrated resistances serve as references against which unknown resistances are measured. The ability to select different known resistances allows for measurement of a wide range of unknown resistances and helps in verifying the linearity and accuracy of the meter bridge setup across different resistance ranges.
The principle of voltage division is fundamental to the meter bridge's operation. The meter bridge wire acts as a voltage divider, where the potential drop across any segment of the wire is proportional to its length. When the bridge is balanced, the voltage division in both arms of the bridge is equal, resulting in no potential difference across the galvanometer. This principle allows us to relate the lengths of wire segments to the resistances in the bridge, forming the basis for resistance measurement.
Using the central portion of the meter bridge wire for measurements is recommended because this region offers the highest sensitivity. Near the center, small changes in the jockey position result in larger changes in the resistance ratio, making it easier to detect the null point accurately. Additionally, any non-uniformities or end effects in the wire's resistance are minimized in the central region, contributing to more accurate measurements.
The cross-sectional area of the meter bridge wire affects its performance by influencing its resistance per unit length. A wire with a larger cross-sectional area has lower resistance per unit length, which can reduce the overall sensitivity of the bridge. However, it also allows for higher current capacity and better heat dissipation. The ideal cross-sectional area balances these factors to provide good sensitivity while avoiding excessive heating or voltage drops.
The galvanometer's internal resistance is important in a meter bridge circuit because it affects the sensitivity of the null detection. A galvanometer with very low internal resistance might allow significant current to flow even when the bridge is slightly unbalanced, reducing the accuracy of the null point determination. Conversely, a very high internal resistance can make the galvanometer too insensitive to small imbalances. The ideal galvanometer should have an internal resistance that allows for sensitive null detection without significantly loading the bridge circuit.
Electrical shielding is important in meter bridge setups to minimize external electromagnetic interference. Shielding can help prevent stray electric fields from inducing currents in the circuit, which could affect the galvanometer readings and lead to inaccurate measurements. Proper shielding, especially around sensitive components like the galvanometer and connecting wires, can improve the accuracy and reliability of meter bridge measurements, particularly when working with very small resistances or in environments with significant electromagnetic noise.
Ensuring good electrical contact at all junction points in a meter bridge setup is crucial for accurate measurements. Poor contacts can introduce additional resistances that are not accounted for in the bridge calculations. These contact resistances can vary unpredictably, leading to inconsistent results. Good electrical contacts minimize these additional resistances, ensure consistent current flow, and maintain the integrity of the potential divisions in the bridge circuit, all of which are essential for precise resistance measurements.
The length of the meter bridge wire affects both its measurement range and accuracy. A longer wire provides a greater range of resistance ratios, allowing for measurement of a wider range of unknown resistances. It also improves accuracy by providing finer gradations in resistance, making it easier to pinpoint the null point. However, a very long wire may introduce issues with uniformity and increase the overall resistance of the bridge, potentially affecting sensitivity. The ideal length balances these factors to provide a good range of measurements with high accuracy.
Using a non-uniform wire in a meter bridge can lead to significant measurement errors. If the wire's resistance per unit length varies along its length, the fundamental assumption of the meter bridge – that resistance is directly proportional to length – is violated. This can result in non-linear potential gradients along the wire, causing inaccurate resistance ratios and incorrect measurements. Non-uniformity can arise from variations in the wire's diameter, composition, or physical condition (e.g., stretching or damage).
Power dissipation in a meter bridge circuit is an important consideration, especially in the bridge wire. As current flows through the wire, it heats up due to its resistance (P = I²R). Excessive heating can change the wire's resistance, leading to measurement errors. It's crucial to limit the current to prevent significant heating while still allowing enough current for accurate null point detection. This balance is part of the reason for using low-voltage power sources and wires with appropriate resistance and current-carrying capacity.
Waiting for the meter bridge to reach thermal equilibrium before taking measurements is important because temperature changes can affect the resistance of the wire and other components. As the circuit heats up due to current flow, resistances may change slightly, leading to drift in the null point. By allowing the system to reach thermal equilibrium, these temperature-induced changes stabilize, resulting in more consistent and accurate measurements. This is particularly important when high precision is required or when measuring small resistances.
The meter bridge is essentially a simplified form of a Wheatstone bridge. Both operate on the principle of balancing resistances in a bridge circuit to measure an unknown resistance. In a Wheatstone bridge, all four arms are separate resistors, while in a meter bridge, two arms are formed by segments of a single resistance wire. The meter bridge simplifies the setup and operation compared to a full Wheatstone bridge, making it more suitable for educational and basic laboratory use, while still employing the same fundamental principles of resistance comparison and balance.
The 'figure of merit' of a galvanometer is a measure of its current sensitivity, typically expressed as the current required to produce a unit deflection. In a meter bridge, a galvanometer with a high figure of merit (high sensitivity) can detect very small current imbalances, allowing for more precise determination of the null point. However, an overly sensitive galvanometer might make it difficult to achieve a stable null reading due to small fluctuations. The ideal galvanometer
Also Read
04 Jul'25 02:56 PM
02 Jul'25 07:59 PM
02 Jul'25 07:35 PM
02 Jul'25 07:02 PM
02 Jul'25 06:02 PM
02 Jul'25 05:52 PM
02 Jul'25 05:52 PM
02 Jul'25 05:52 PM
02 Jul'25 05:52 PM
02 Jul'25 05:51 PM