Ohm's Law - Definition, Formula, Applications, FAQs
Ohm's law describes the electric current and Potential Difference relationship in a wire or a conductor. According to it, the current through most conductors is directly proportional to the applied voltage, provided the Physical property(temperature) is unchanged. This was first confirmed by German physicist Georg Simon Ohm and is a basic principle of electricity. Ohm's law finds extensive application in experiments and real-life applications to compute current, voltage or resistance in electric circuits. It is also utilized in designing electrical devices and determining how well materials allow electricity to flow, thus being a key principle in experiments and real-world applications. In this topic page, will study definition of Ohm's law, verification of Ohm's law, formulas, applications, and examples of Ohm's law.
This Story also Contains
- What is Ohm’s law?
- Verification of Ohm's Law
- Resistance
- Applications of Ohm’s law:
- Uses of Ohm’s law:
- Numericals on Ohm’s law
Also check-
What is Ohm’s law?
If the physical conditions remain unchanged (such as temperature), the potential difference across the two ends of a conductor is directly proportional to the electric current flowing through it.
$
\begin{aligned}
& V \propto I \\
& V=R I
\end{aligned}
$
where, $R$ is the constant of proportionality and is called the resistance of the conductor.
It is the property of a conductor to resist the flow of charges through it.
Verification of Ohm's Law
It can be verified with the help of an activity. Set up an electric circuit containing a resistor $R$ (e.g., a metal wire) as shown below.
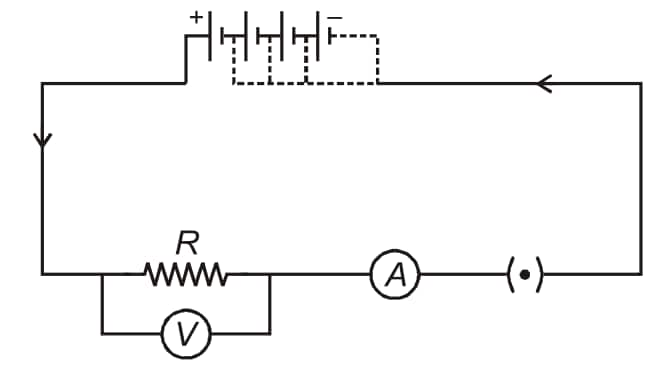
An ammeter $(A)$ and a voltmeter $(V)$ are connected in the circuit so as to measure current across the resistor and the potential difference across it respectively. Note down the readings of $A$ and $V$ for the values of current through the resistance and potential difference across it.
Connect one more cell in the circuit and again note the corresponding readings of ammeter and voltmeter. Repeat the procedure for different number of cells connected in the circuit.
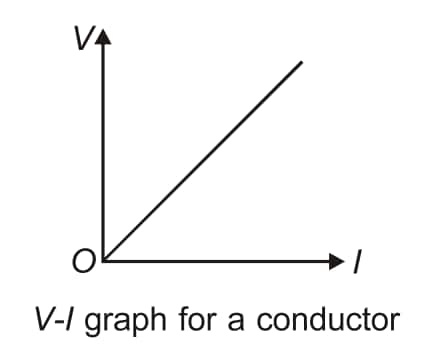
Find out the ratio of $\frac{V}{I}$ for every set of readings of the voltmeter and the ammeter. You will see the ratio comes out to be almost the same everytime. This ratio is called the resistance of the wire. Plot a graph between $V$ and $I$. The nature of the graph is as shown in the figure below.
By definition, the ratio $\frac{V}{l}$ is the electric resistance $R$ of the conductor.
$
R=\frac{V}{I}=\text { constant }
$
Resistance
Resistance is the property of a material that opposes the flow of electric current through it. When an electric current passes through a conductor, some energy is used to overcome this opposition, and it is often converted into heat.
Resistance is denoted by the letter $\mathbf{R}$. The SI unit of resistance is the ohm ( $\mathbf{\Omega}$ ).
The resistance of a conductor depends on:
1. Length (L): Resistance increases with length.
2. Area of cross-section (A): Resistance decreases with an increase in area.
3. Material: Different materials have different resistivities.
4. Temperature: For most conductors, resistance increases with temperature.
The relationship between resistance, voltage, and current is given by Ohm's Law:
$
R=\frac{V}{I}
$
where $V$ is the potential difference and $I$ is the current.
Also read -
Applications of Ohm’s law:
At constant temperature, ohm’s law can be applicable. Electricity's fundamental law is Ohm’s law. The applications of Ohm’s law are,
- In an electric circuit, the current, potential difference and resistance can be determined.
- The power efficiency of an electric circuit can be calculated.
- Ohm’s law is applicable to the linear elements
Failures of Ohm’s law:
- The behaviour of devices such as diodes and transistors is not explained by Ohm’s law.
- Ohm’s law does not give the expected result at the variable temperature.
- Ohm’s law cannot be applicable to non-linear elements.
Uses of Ohm’s law:
- We may control the speed of the fans in our residences by pushing the regulator back and forth.
- The current going through the fan is regulated here by regulating the resistance via the regulator.
- Using Ohm’s law, we can determine the resistance, current, and consequently power flowing for any given input value.
Numericals on Ohm’s law
1. A 12-clombs charge passes through a bulb in 5 seconds. How much current passes through the bulb?
Solution:
Charge, Q=12 C
Time, t=5s
To find the current:
I=Q/t
I=12/5
I=2.4 A
Hence, the current flows through the bulb is 2.4 A
2. Moving a charge of 10 C across two locations in a circuit requires 100 J of labour. What could be the difference between the two points?
Solution:
Charge, Q=10 C
Work done, W=100 J
To get the possible difference between the points, do the following:
V=work done (w)/charge (Q)
V=100/10
V=10 Volt
Hence, the potential difference between the two points is 10 Volt.
3. Calculate the resistance of a conductor with a 2 A current and a 30 V potential difference between its ends.
Solution:
Current through the conductor, I=2 A
The potential difference between its ends, V=30 V
From Ohm’s law,
R=V/I
R=30/2
R=15 Ω
Hence, the resistance of the conductor is 15 Ω
4. A lamp of resistance 70 Ω draws a current of 0.75 A . Find the voltage
Solution:
Resistance, R=70 Ω
Current, I=0.75 A
To find the voltage:
From Ohm’s law,
V=IR
V=0.75(70)
V=52.5 V
Hence, the voltage of a lamp is 52.5 V
5. A bulb with a resistance of 400 ohms is connected to a 220 V power supply. Calculate the magnitude of the current
Solution:
Resistance, R=400 Ω
The potential difference, V=220 V
To find the magnitude of the current:
From Ohm’s law,
V=IR
I=V/R
I=220/400
I=0.55 A
Hence, the magnitude of the current is 0.55 A
6. When the potential across the filament of a bulb is 100 V, the current through it is found to be 2 A. Find the resistance of the filament.
Solution:
The potential across the filament, V=100 V
The flow of current, I=2 A
To find the resistance of the filament:
From Ohm’s law,
V=IR
R=V/I
R=100/2
R=50 Ω
Hence, the resistance of the filament is 50 Ω
7. A resistance of 15 Ω carries a current of 5 A. Calculate the voltage that has built up across the resistor.
Solution:
Resistance, R=15 Ω
Current, I=5 A
To find the voltage developed across the resistor:
From Ohm’s law,
V=IR
V=(5)(15)
V=75 V
Hence, the voltage across the resistor is 75 V
8. A lamp draws a current of 0.91 A with a potential difference of 110 V. What is the resistance in the lamp?
Solution:
Current, I=0.91 A
The potential difference, V=110 V
To find the resistance in the lamp:
From ohm’s law,
V=IR
R=V/I
R=110/0.91
R=121 Ω
Hence, the resistance in the lamp is 121 Ω
Also Read:
- NCERT Solutions for Class 12 Physics Chapter 3 Current Electricity
- NCERT Exemplar Class 12 Physics Solutions Chapter 3 Current Electricity
- NCERT notes Class 12 Physics Chapter 3 Current Electricity
NCERT Physics Notes:
Frequently Asked Questions (FAQs)
According to Ohm’s law, the steady current I flowing through a conductor is proportional to the potential difference V between the conductor's two ends at constant temperature..The link between an electric current and the potential difference is defined by Ohm’s law.
Formula of ohm’s law, V=IR
At constant temperature, ohm’s law can be applicable. Electricity's fundamental law is Ohm’s law. The applications of ohm’s law are,
In an electric circuit, the current, potential difference and resistance can be determined.
The power efficiency of an electric circuit can be calculated.
Ohm’s law is applicable to the linear elements
We may control the speed of the fans in our residences by pushing the regulator back and forth.
The current going through the fan is regulated here by regulating the resistance via the regulator.
Using Ohm’s law, we can determine the resistance, current, and consequently power flowing for any given input value.