Derivation of Equation of Motion - 3 Equations of Motion

Definition of Equations of Motion

Equations of Motion in physics describe how a body moves with uniform acceleration. These equations show the relationship between displacement (s), velocity (u,v), acceleration (a), and time (t).

There are three equations of motion:

First Equation of Motion

$v=u+a t$
It gives the final velocity of an object.

Second Equation of Motion
$s=u t+\frac{1}{2} a t^2$
It gives the displacement of an object.

Third Equation of Motion

$v^2=u^2+2 a s$

It relates velocity and displacement without involving time.

Derivation of Equations of Motion

The equations of motion describe the motion of an object moving with uniform acceleration. These equations can be derived using different approaches, depending on the level of understanding and mathematical tools used.

The equations of motion are derived by the following three methods:

• Simple Algebraic Method – Uses basic definitions of velocity and acceleration.
• Graphical Method – Uses velocity–time graphs to obtain equations.
• Calculus Method – Uses differentiation and integration for a more advanced derivation.

Derivation of First Equation of Motion

The first equation of motion is:

$
v=u+a t
$

where
$u=$ initial velocity
$v=$ final velocity
$a=$ acceleration
$t=$ time
1. Derivation by Algebraic Method

Acceleration is defined as the rate of change of velocity.

$
\begin{gathered}
a=\frac{\text { change in velocity }}{\text { time }} \\
a=\frac{v-u}{t}
\end{gathered}
$

Rearranging,

$
\begin{aligned}
& v-u=a t \\
& v=u+a t
\end{aligned}
$

2. Derivation by Graphical Method
Draw a velocity-time graph for uniform acceleration.

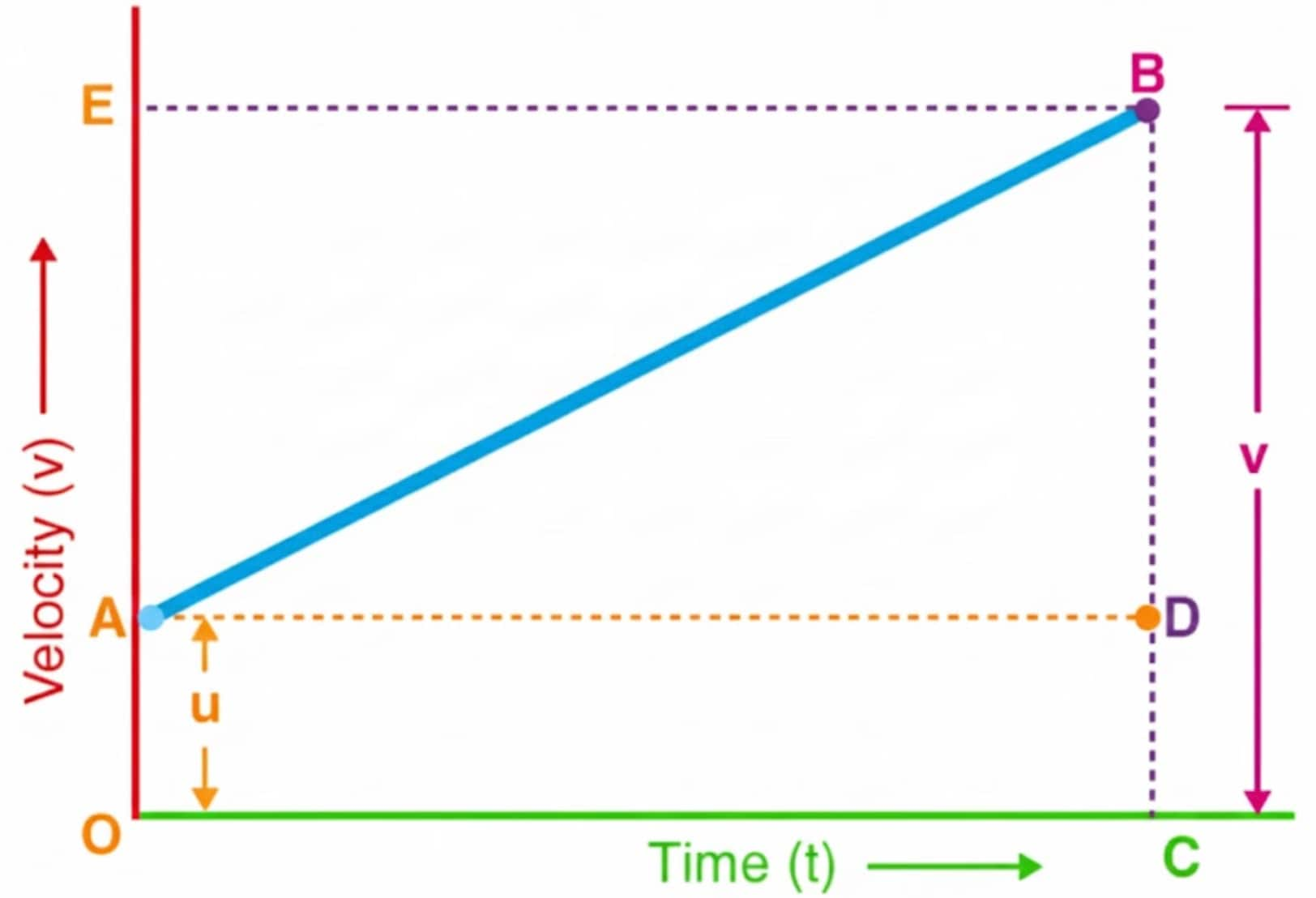
Initial velocity $=u$
Final velocity $=v$
Time $=t$

From the graph, slope = acceleration

$
\text { slope }=\frac{v-u}{t}
$

But slope $=$ acceleration $a$

$
\begin{aligned}
& a=\frac{v-u}{t} \\
& v=u+a t
\end{aligned}
$

3. Derivation by Calculus Method

Acceleration is defined as:

$
\begin{aligned}
a & =\frac{d v}{d t} \\
d v & =a d t
\end{aligned}
$

Integrating both sides,

$
\begin{gathered}
\int d v=\int a d t \\
v=a t+C
\end{gathered}
$

When $t=0, v=u$

$
\begin{gathered}
u=C \\
v=u+a t
\end{gathered}
$

NCERT Physics Notes :

• NCERT Notes class 11 physics
• NCERT Notes class 12 physics
• NCERT Notes for all subject

Derivation of Second Equation of Motion

The second equation of motion is:

$
s=u t+\frac{1}{2} a t^2
$

where
$s=$ displacement
$u=$ initial velocity
$a=$ acceleration
$t=$ time
1. Derivation by Algebraic Method

Average velocity for uniform acceleration:

$
v_{\text {avg }}=\frac{u+v}{2}
$

Displacement:

$
\begin{aligned}
s & =v_{\text {avg }} \times t \\
s & =\frac{u+v}{2} \times t
\end{aligned}
$

From first equation of motion:

$
v=u+a t
$

Substitute $v$ :

$
\begin{gathered}
s=\frac{u+(u+a t)}{2} \times t \\
s=\frac{2 u+a t}{2} \times t \\
s=u t+\frac{1}{2} a t^2
\end{gathered}
$

2. Derivation by Graphical Method

Draw a velocity-time graph.

Initial velocity $=u$
Final velocity $=v$
Time $=t$

Displacement = area under velocity-time graph
Area $=$ area of rectangle + area of triangle

$
s=(u \times t)+\frac{1}{2}(v-u) t
$

Using $v-u=a t$ :

$
s=u t+\frac{1}{2} a t^2
$

3. Derivation by Calculus Method

Velocity:

$
v=\frac{d s}{d t}
$

From first equation:

$
\begin{gathered}
v=u+a t \\
\frac{d s}{d t}=u+a t \\
d s=(u+a t) d t
\end{gathered}
$

Integrating both sides:

$
\begin{gathered}
\int d s=\int(u+a t) d t \\
s=u t+\frac{1}{2} a t^2+C
\end{gathered}
$
When $t=0, s=0$

$
\begin{gathered}
C=0 \\
s=u t+\frac{1}{2} a t^2
\end{gathered}
$

Derivation of Third Equations of Motion:

The third equation of motion is:

$
v^2=u^2+2 a s
$

where
$u=$ initial velocity
$v=$ final velocity
$a=$ acceleration
$s=$ displacement
1. Derivation by Algebraic Method

From the first equation of motion:

$
v=u+a t
$

Rearranging:

$
t=\frac{v-u}{a}
$

From the second equation of motion:

$
s=u t+\frac{1}{2} a t^2
$

Substitute $t$ :

$
s=u\left(\frac{v-u}{a}\right)+\frac{1}{2} a\left(\frac{v-u}{a}\right)^2
$

Simplifying:

$
\begin{aligned}
2 a s= & 2 u(v-u)+(v-u)^2 \\
& 2 a s=v^2-u^2 \\
& v^2=u^2+2 a s
\end{aligned}
$

2. Derivation by Graphical Method
Draw a velocity-time graph.

Displacement $s=$ area under the graph

$
s=\frac{1}{2}(u+v) t
$

From acceleration:

$
a=\frac{v-u}{t} \Rightarrow t=\frac{v-u}{a}
$

Substitute $t$ :

$
\begin{aligned}
s= & \frac{1}{2}(u+v)\left(\frac{v-u}{a}\right) \\
& 2 a s=v^2-u^2 \\
& v^2=u^2+2 a s
\end{aligned}
$

3. Derivation by Calculus Method

Acceleration:

$
a=\frac{d v}{d t}
$

But,

$
v=\frac{d s}{d t}
$

So,

$
\begin{gathered}
a=v \frac{d v}{d s} \\
v d v=a d s
\end{gathered}
$

Integrating both sides:

$
\begin{gathered}
\int v d v=\int a d s \\
\frac{v^2}{2}=a s+C
\end{gathered}
$

When $s=0, v=u$

$
\begin{gathered}
C=\frac{u^2}{2} \\
v^2=u^2+2 a s
\end{gathered}
$

Also, check-

• NCERT Exemplar Class 11th Physics Solutions
• NCERT Exemplar Class 12th Physics Solutions
• NCERT Exemplar Solutions for All Subjects