Derivation of Centripetal Acceleration - Detailed Guide
Imagine driving around a curve and feeling a pull outward—that's centripetal acceleration in action, a key concept in circular motion. It helps explain how Forces work on a vehicle during turns. Understanding this can make driving safer, especially when navigating curves at higher speeds. In this report, we explore the role of centripetal acceleration, factors that affect it like speed and friction, and practical tips for handling turns. In this article we will be studying the centripetal acceleration derivation. This concept, covered in Class 11 Physics under circular motion, derivation of centripetal acceleration is essential for board exams and competitive exams like JEE Main, NEET, BITSAT, and others. Between 2013 and 2023, five questions on this topic have appeared in JEE Main.

Centripetal Acceleration Derivation
Consider a body of mass ‘m’ moving on the circumference of a circle of radius ‘r’ with a velocity ‘v’. A force F is then applied to the body. And this force is given by
F = ma
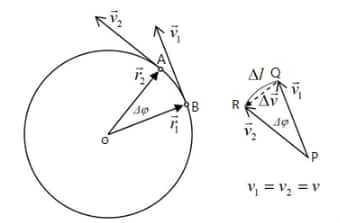

Where, a= acceleration which is given by the rate of change of velocity with respect to time.
Consider the triangles $\triangle O A B$ and $\triangle P Q R$, then:
$
\Delta v_{A B}=\frac{v}{r}
$
Clearly, from the diagram (not shown here), the arc length $A B=v \Delta t$.
Now, we have:
$
\frac{\Delta v}{v \Delta t}=\frac{v}{r}
$
Simplifying this:
$
\frac{\Delta v}{\Delta t}=\frac{v^2}{r}
$
Thus, the centripetal acceleration equation is:
$
a=\frac{v^2}{r}
$
Note: The direction of centripetal acceleration(& force) is towards the centre of the circle.
Now, let's move to another part of this article which is Centripetal Force
What is the direction of centripetal acceleration?
The direction of centripetal acceleration and also force is towards the centre of the circle.
Recommended Topic Video
Solved Examples of Centripetal Acceleration
Q.1 A car moves in a circular path of radius $\mathbf{2 0 ~ m}$ with a speed of $\mathbf{1 0 ~ m} / \mathbf{s}$.
Find its centripetal acceleration.
Solution:
Using formula,
$
\begin{gathered}
a_c=\frac{v^2}{r} \\
a_c=\frac{(10)^2}{20}=\frac{100}{20}=5 \mathrm{~m} / \mathrm{s}^2
\end{gathered}
$
Centripetal acceleration $=5 \mathrm{~m} / \mathrm{s}^2$.
Q.2 A stone tied to a string rotates in a horizontal circle of radius 0.5 m with an angular speed of 6 rad/s. Calculate centripetal acceleration.
Solution:
Using formula,
$
\begin{gathered}
a_c=\omega^2 r \\
a_c=(6)^2 \times 0.5=36 \times 0.5=18 \mathrm{~m} / \mathrm{s}^2
\end{gathered}
$
Centripetal acceleration $=18 \mathrm{~m} / \mathrm{s}^2$.
Q.3 A fan blade rotates with an angular speed of $\mathbf{2 0 ~ r a d} / \mathrm{s}$. If the edge of the blade is $\mathbf{0 . 3 ~ m}$ from the centre, find the centripetal acceleration of the tip.
Solution:
$
\begin{gathered}
a_c=\omega^2 r \\
a_c=(20)^2 \times 0.3=400 \times 0.3=120 \mathrm{~m} / \mathrm{s}^2
\end{gathered}
$
Centripetal acceleration $=120 \mathrm{~m} / \mathrm{s}^2$.
Also, check-
Frequently Asked Questions (FAQs)
We start with the formula for centripetal force:
F=mv2r
Also, from Newton's 2nd law:
F=ma
We can express acceleration as:
a=Fm
Substituting the value of F from the centripetal force equation:
a=mv2rm
Simplifying it:
a=v2r
Thus, the centripetal acceleration is:
a=v2r
Proof:
1. F=mv2r (using centripetal force)
2. F=ma (using Newton's 2nd law)
We can rewrite this as:
3. a=Fm
Substituting the value of F from equation (1) into equation (3):
4. a=mv2r÷m
Simplifying:
5. a=v2r
This is the required expression for acceleration in circular motion.
Centripetal acceleration is the acceleration of a body that is travelling across a circular path. When a body undergoes a circular motion, its direction constantly changes and thus its velocity changes (velocity is a vector quantity) which produces an acceleration.Derivation:
F=mv2r (using centripetal force)
F=ma (using Newton's second law)
We can rewrite this as:
a=Fm
Substituting the value of F
$a=\frac{m v^2}{r} \div m$
a=v2r
Thus, the centripetal acceleration is given by a=v2r.
Derivation for centripetal force is given in this article.