Difference Between Distance and Displacement
The concepts of distance and displacement are considered crucial in motion in the study of physics. In everyday discussions, most of the time, distance and displacement appear in one category, but in science, these words differ from each other. The main difference between them is that distance is a scalar quantity or a measure of total path that has been covered by an object; whereas, displacement is a vector quantity, which is defined as the length of the shortest path to "follow" direction between the starting and the ending point.
This Story also Contains
- What is Distance
- What is Displacement
- Distance and Displacement Formulas
- Points to ponder:
- Difference between Distance and Displacement
These concepts are not only important for higher class but also crucial for school learning. Be it exams to prepare for like JEE Main or NEET or even boards like CBSE, ICSE, and even state level such as Maharashtra Board, knowing distance and displacement goes a long way in falling in kinematics, which is actually an opening chapter in physics, functional in preparing a learner for serious battling in competition. There are many versions of this topic in both school and entrance tests, so understanding the definitions and examples of real-life applications is crucial.
What is Distance
- The length of the path traversed is called path length or distance.
- The distance is a scalar quantity — a quantity that has a magnitude only and no direction
- SI unit of Distance: m
- Dimension of Distance: [Pathlength]=[L]
What is Displacement
- It is the shortest straight line path between the initial and final position.
- Displacement has both magnitude and direction.
- The magnitude of displacement may or may not be equal to the path length (distance) traversed by an object or in other words, the distance travelled is always greater than or equal to the magnitude of displacement.
Distance $\geq \mid$ Displacement $\mid$
For example, for the motion of the car from O to P, the path length is +360 m and the displacement is +360 m. In this case, the magnitude of displacement (360 m) is equal to the path length (360 m). But consider the motion of the car from O to P and back to Q. In this case, the path length = (+360 m) + (+120 m) = + 480 m. However, the displacement = (+240 m) – (0 m) = + 240 m. Thus, the magnitude of displacement (240 m) is not equal to the path length (480 m).
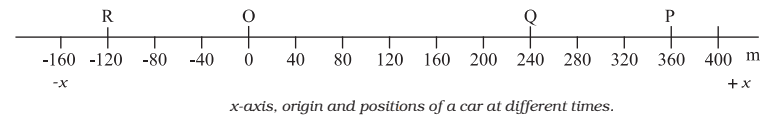
- The magnitude of the displacement for a course of motion may be zero but the corresponding path length is not zero.
- For example, if the car starts from O, goes to P and then returns to O, the final position coincides with the initial position and the displacement is zero. However, the path length of this journey is OP + PO = 360 m + 360 m = 720 m.
- SI unit of Displacement: m
- Dimension of Displacement: [Displacement]=[L]
Distance and Displacement Formulas
Distance (d): Total path covered.
$
d=\text { sum of all path lengths }
$
Displacement ( $\Delta \mathbf{x}$ ): Shortest straight-line distance between final and initial position, with direction.
$
\Delta x=x_{\text {final }}-x_{\text {initial }}
$
SI Unit: Both are measured in metres (m).
Example: Meera walks 100 m forward and 60 m back.
Distance $=100+60=160 \mathrm{~m}$
Displacement $=100-60=40 \mathrm{~m}$ forward
Points to ponder:
- The displacement depends only on the endpoints; the path length (as the name implies) depends on the actual path.
- In one dimension, the two quantities are equal only if the object does not change its direction during the course of motion.
- In all other cases, the path length is greater than the magnitude of displacement
- The magnitude of the displacement for a course of motion may be zero but the corresponding path length is not zero.
Key points to remember:
- The coordinate system along with a clock constitutes a frame of reference.
- If one or more coordinates of an object change with time, we say that the object is in motion
- The description of an event depends on the frame of reference chosen for the description.
- The magnitude of displacement may or may not be equal to the path length (distance) traversed by an object or in other words, the distance travelled is always greater than or equal to the magnitude of displacement.
Distance $\geq \mid$ Displacement $\mid$ - If an object moving along a straight line covers equal distances in equal intervals of time, it is said to be in uniform motion along a straight line.
Difference between Distance and Displacement
The difference between distance and displacement is given in the table.
| Sl. No. | Different properties | Distance | Distance |
| 1. | Definition | The distance between any two points is the total length of the path. | The direct length between any two points measured along the shortest path between them is called displacement. |
| 2. | Denotation | d | s |
| 3. | Direction Consideration | The direction is ignored when calculating distance. | The direction is taken into account when calculating displacement. |
| 4. | Quantity | The magnitude, not the direction, determines the value of a scalar quantity. | Because it depends on both magnitude and direction, displacement is a vector quantity. |
| 5. | Route Information | The term "distance" refers to the specific route information used when travelling from one location to another. | Because displacement only refers to the quickest way, it does not provide entire route information. |
| 6. | Formula | speed × time | velocity ×time |
| 7. | Possible values | Only positive numbers can be used in the distance. | Positive, negative, or even zero displacement is possible. |
| 8. | Measurement in non- non-straight path | A non-straight path can be used to calculate the distance. | Only a straight road may be used to quantify displacement. |
| 9. | Indication | An arrow does not represent distance. | An arrow is always used to denote displacement. |
| 10. | Path dependence | The distance is determined by the path followed, and it varies depending on the way taken. | Displacement is independent of the path and solely depends on the body's initial and ending positions. |
Also read :
Frequently Asked Questions (FAQs)
The term "distance" which refers to "how much ground an object has covered" during its travel. The overall change in position of an object is described by displacement, which is a vector quantity that describes "how far an object is out of place."
Distance is the length of the whole path taken by the body between the initial and end sites, therefore distance equals displacement if the body moves in a straight line.
Use the distance formula d = s * t, or distance equals speed times time
The length of the line segment connecting two places is called the distance between them. The length of the line segment connecting the specified two coordinates can be used to compute the distance between two points in coordinate geometry.
The shortest distance between the surfaces of two parallel planes is known as the distance between them. Consider this: if the planes are not parallel, they will ultimately intersect. If they cross, they have no distance — 0 distance — between them on that line of crossing.