Electric Flux - Definition, Formula, FAQs

Electric flux measures how an electric field passes through an area that was defined already. Electric flux within electromagnetism is very important because it helps in proper comprehension of how electric fields come into contact with or affect surfaces. Over the last ten years of the JEE Main exam (from 2013 to 2023), nine questions have been asked on this concept. In this article, we will discuss what is electric flux class 12, the symbol of electric flux, the electric flux formula, properties of electric flux, Gauss's law, the SI unit, the dimension of electric flux, the derivation of electric flux through a closed surface and electric flux density.

This Story also Contains

1. What is Electric Flux Class 12?
2. Electric Flux Formula
3. SI Unit of Electric Flux and Dimensional Formula
4. Properties of Electric Flux
5. Electric Flux Density
6. Gauss Law
7. Derivation of Electric Flux Through a Closed Surface
8. Solved Examples Based on Electric Flux

What is Electric Flux Class 12?

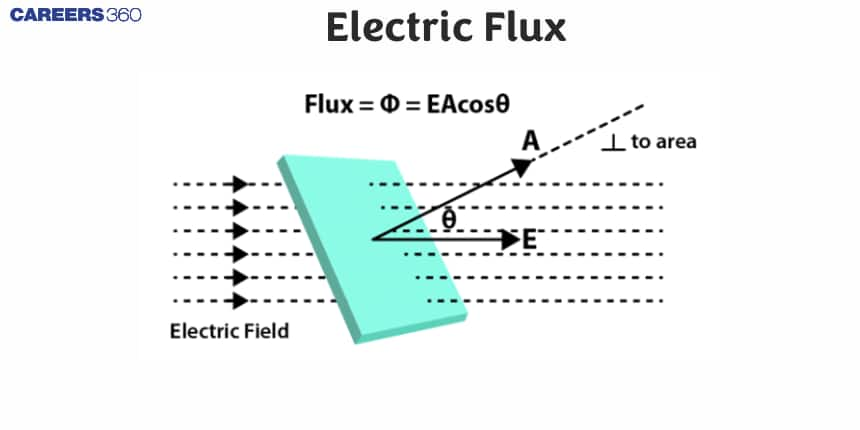
Electric flux definition: Electric flux is the rate of flow of electric lines of force across a particular area chosen as a surface.

Let us consider an electric field that is uniform in both magnitude and direction. Let these field lines penetrate a rectangular surface of area A whose plane is oriented perpendicular to the field lines. The number of electric field lines per unit area is proportional to the magnitude of the electric field. So the total number of lines penetrating is proportional to $E.A$.

The symbol of electric flux is the Greek letter phi with subscript $E$. So electric flux symbol is $\Phi_E$.

Electric Flux Formula

The magnitude of this product is known as Electric flux, which is denoted by

$\phi_E=E A$

So,

The electric flux through an area is the number of electric field lines passing normally through the area.

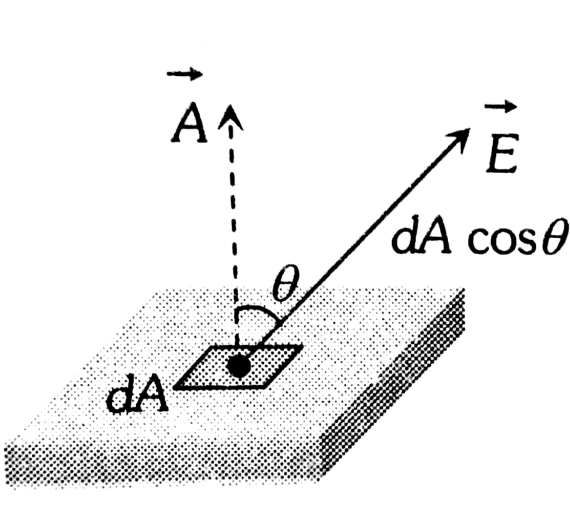
The formula of electric flux through an area, dA is given by

$d \phi=\vec{E} \cdot \vec{d} A=E d A \cos \theta$

here, $\theta$ is the angle between the area vector and the electric field.

Total flux through area A is

$\phi=\int \vec{E} \cdot \vec{d} A$

SI Unit of Electric Flux and Dimensional Formula

Flux is a scalar quantity so they can be added algebraically.

The SI unit of electric flux is newton meter squared per coulomb $\left(\mathrm{N} \cdot \mathrm{m}^2 / \mathrm{C}\right)$ and volt meter $(\mathrm{V} \cdot \mathrm{m})$

Dimensional Formula

$E$ (electric field) has the dimensional formula $\left[M^1 L^1 T^{-3} I^{-1}\right]$.
$A$ (area) has the dimensional formula $\left[L^2\right]$.

Electric flux= $\mathbf{E} \cdot \mathbf{A}$

$\Phi_E=\left[M^1 L^1 T^{-3} I^{-1}\right] \times\left[L^2\right]$

thus dimension of electric flux are $\left[M^1 L^3 T^{-3} I^{-1}\right]$

Properties of Electric Flux

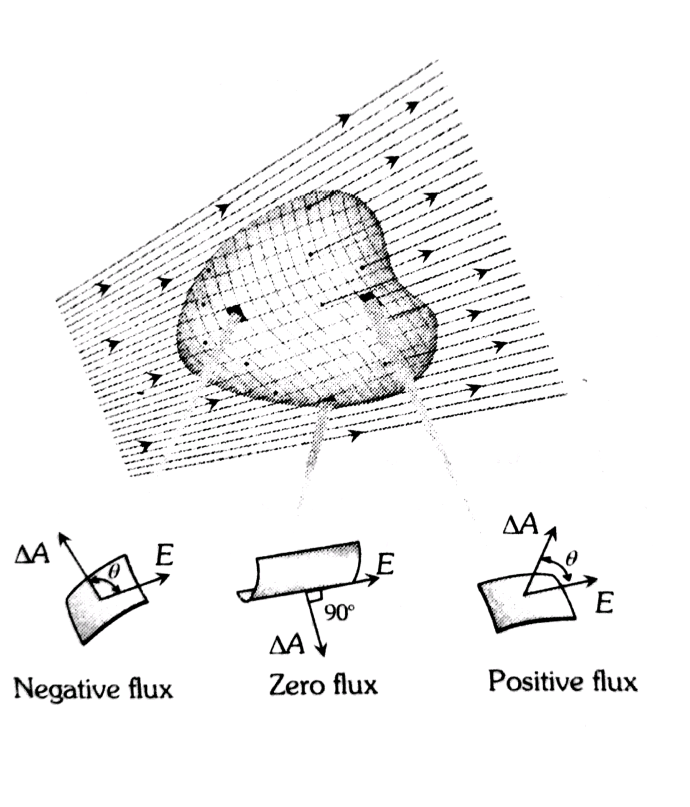
1. The electric flux is dependent on the strength of the electric field and the field passing area.
2. The flux is maximum at an angle $\theta=0^{\circ}$ ( the field lines are perpendicular to the surface)
3. The flux is minimum (zero) at an angle $\theta=90^{\circ}$ ( the field lines are parallel to the surface)
4. If the field lines are pointed outwards from the surface then the electric flux is positive. If they are pointed inward to the surface, the electric flux is negative.
5. The total flux through a closed surface with no net charge is zero.

Electric Flux Density

Electric flux density is the amount of flux passing through a unit area in an electric field. Electric flux density is also called an electric displacement field. It is given as,

$$
\mathbf{D}=\epsilon \mathbf{E}
$$

where,

• D is the electric flux density
• $\epsilon$ is the permittivity of the medium
• E is the electric field intensity

Gauss Law

Gauss's law states that in a closed surface, the electric flux is directly proportional to the total charge enclosed by the surface. Mathematically it can be expressed as,

$$
\oint \mathbf{E} \cdot d \mathbf{A}=\frac{Q_{\mathrm{enc}}}{\epsilon_0}
$$

where,

• $\oint \mathbf{E} \cdot d \mathbf{A}$ is the total electric flux through a closed surface.
• $Q_{\mathrm{enc}}$ is the total electric charge enclosed within the surface.
• $\epsilon_0$ is the permittivity of free space

Derivation of Electric Flux Through a Closed Surface

To understand this concept, let us take an example

Consider a cylindrical surface of radius R, length $l$, in a uniform electric field E. Compute the electric flux if the axis of the cylinder is parallel to the field direction. For this we can divide the entire surface into three parts, right and left plane faces and a curved portion of its surface. Hence, the surface integral consists of the sum of the three terms:

$\phi_E=\oint E \cdot d A=\oint_{\text {left end }} E \cdot d A+\oint_{\text {right end }} E \cdot d A+\oint_{\text {curved }} E \cdot d A$

Here, the left end and electric field are making 180^o, and the right end and the electric field are making $0^{\circ}$. Also one can notice that the curved surface is making 90^o with the direction of electric field. So,

$\begin{aligned}\left(\phi_E\right)_{\text {left end }} & =\oint_{\text {left end }} \vec{E} \cdot \overrightarrow{d A}=\oint_{\text {left end }} \vec{E} \overrightarrow{d A} \cos 180^{\circ}=-E \pi R^2 \\ \left(\phi_E\right)_{\text {right end }} & =\oint_{\text {right end }} \vec{E} \cdot \overrightarrow{d A}=\oint_{\text {right end }} \vec{E} \vec{A} \cos 0^{\circ}=E \pi R^2 \\ \left(\phi_E\right)_{\text {curved }} & =\oint_{\text {curved surfice }} \vec{E} \cdot \overrightarrow{d A}=\oint_{\text {curved surface }} E d A\left(\cos 90^{\circ}\right)=0 \\ \text { Total flux } & =\left(\phi_E\right)_{\text {right end }}+\left(\phi_L\right)_{\text {left end }}+\left(\phi_E\right)_{\text {curved surface }} \\ & =\left(+E \pi R^2\right)+\left(-E \pi R^2\right)+0=0\end{aligned}$

Similarly, we can find the electric flux through any closed surface by an electric field.

Also, read

• NCERT Exemplar Solutions for All Subjects
• NCERT Notes For All Subjects
• NCERT Solutions for All Subjects

Solved Examples Based on Electric Flux

Example 1: A cone of base radius $R$ and height $h$ is located in a uniform electric field $\vec{E}$ parallel to its base. The electric flux entering the cone is :
1) $\frac{1}{2} E h R$
2) $E h R$
3) $2 E h R$
4) $4 E h R$

Solution:

Electric field $\vec{E}$ through any area $\vec{A}$ -

$\begin{aligned} & \phi=\vec{E} \cdot \vec{A}=E A \cos \Theta \\ & \text { S.I unit }-(\text { volt }) m \text { or } \frac{N-m^2}{c}\end{aligned}$

wherein

Area of $\Delta$ facing $=\frac{1}{2} \times h \times 2 R$

$
\therefore \phi=E h R
$

Example 2: The electric field in a region of space is given by, $\vec{E}=E_0 \hat{i}+2 E_0 \hat{j}$ where $\mathrm{E}_0=100 \mathrm{~N} / \mathrm{C}$. The flux of this field through a circular surface of radius 0.02 m parallel to the Y -Z plane is nearly :
1) $0.125 \mathrm{Nm}^2 I C$
2) $0.02 \mathrm{Nm}^2 I C$
3) $0.005 \mathrm{Nm}^2 I C$
4) $3.14 \mathrm{Nm}^2 I \mathrm{C}$

Solution:

$\begin{aligned} & \vec{E}=E_0 \hat{i}+2 E_0 \hat{J} \\ & E_0=100 \mathrm{~W} / \mathrm{C} \\ & \vec{E}=100 \hat{i}+200 \hat{J} \\ & A=\pi r^2=\frac{22}{7} \times 0.02 \times 0.02 \\ & A=1.25 \times 10^{-3} \hat{i} \mathrm{~m}^2 \\ & \therefore \text { New flux } \therefore \phi=E A \cos \theta \\ & \phi=(100 \hat{i}+200 \hat{J}) .1 .25 \times 10^{-3} \hat{i} \\ & \phi=1.25 \times 10^{-1} \mathrm{Nm}^2 / \mathrm{c} \\ & =0.125 \mathrm{Nm}^2 / \mathrm{C}\end{aligned}$

Hence, the answer is the option (1).

Example 3: A cylinder of radius $R$ and length $L$ is placed in a uniform electric field $E$ parallel to the cylinder axis. The total flux for the surface of the cylinder is given by
1) $2 \pi R^2 E$
2) $\pi R^2 / E$
3) $\left(\pi R^2-\pi R\right) / E$
4) zero

Solution:

Electric field E through any area A

$$
\begin{aligned}
& \phi=\vec{E} \cdot \vec{A}=E A \cos \Theta \\
& \text { S.I unit }-(\text { volt }) m \text { or } \frac{N-m^2}{c}
\end{aligned}
$$

wherein

Flux through surface $\mathrm{A} \quad \phi_A=E \times \pi R^2$ and $\phi_B=-E \times \pi R^2$
Flux through cursurfacesaceC $=\int E d s=\int E d s \cos 90^{\circ}=0$

Total flux through cylinder $=\phi_A+\phi_B+\phi_C=0$

Example 4: Electric field at a point varies as $r^0$ for
1) An electric dipole
2) A point charge
3) A plane infinite sheet of charge
4) A line charge of infinite length

Solution:

Electric field E through any area A

$\begin{aligned} & \phi=\vec{E} \cdot \vec{A}=E A \cos \Theta \\ & \text { S.I unit }-(\text { volt }) m \text { or } \frac{N-m^2}{c}\end{aligned}$

wherein

$E=\frac{\sigma}{\left(2 \varepsilon_0\right)}$

Example 5: Total electric flux coming out of a unit positive charge put in air is:

1) $\varepsilon_0$
2) $\varepsilon_0^{-1}$
3) $\left(4 p \varepsilon_0\right)^{-1}$
4) $4 \pi \varepsilon_0$

Solution:

Flux may be Positive Negative or zero

For closed body.

wherein

$\text { Total flux coming out from unit charge }=\vec{E} d \vec{s}=1 / \varepsilon_0=\varepsilon_0^{-1}$