Electric Field

When we circle around a charged particle or object charged particles are forced. It is like an invisible force field that can make other charges. The formation or end of such a field’s force lines represents its power and orientation respectively; they also indicate the path along which there would be motion if there were a positive test charge within the given field. The understanding of electric forces operating by the use of electric field lines is a major aspect of physics.

This Story also Contains

1. Electric field and electric lines of force:
2. Electric Field Intensity:
3. Electric field due to a point charge:
4. Solved Examples Based on Electric Field
5. Summary

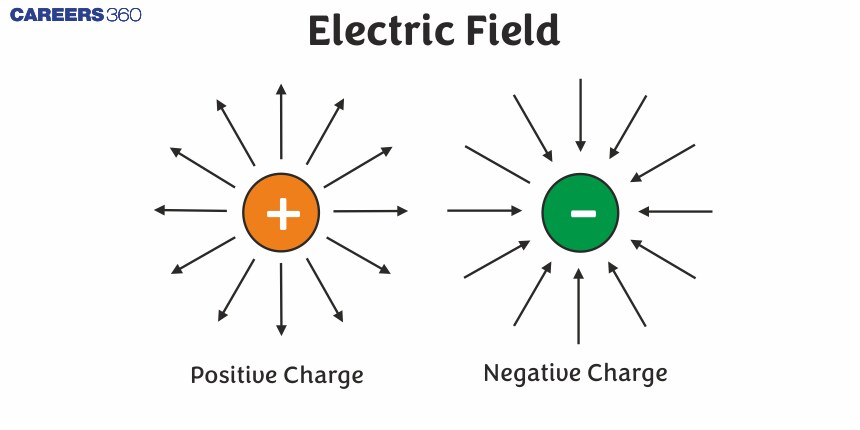
In this article, we will discuss the electric field. An electric field is considered one of the main ideas that is very necessary to understand different things that happen around us both in the past and the present day. This is the area which surrounds a charged particle and through which other charges feel the force. In order to pass NEET or JEE Main exams, it is necessary to study what the electric field means since it is needed when studying other topics such as electrostatics and electromagnetism. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of seventeen questions have been asked on this concept. And for NEET three questions were asked from this concept.

Electric field and electric lines of force:

The space around a charge in which another charged particle experiences a force is said to have an electric field in it.

Electric Field Intensity:

The electric field intensity at any point is defined as the force experienced by a unit of positive charge placed at that point.

$
E=\frac{F}{q_0}
$

where F is the force experienced by q 0 . The SI unit

$
\frac{\text { Newton }}{\text { Columb }}=\frac{\text { Volt }}{\text { meter }}=\frac{\text { Joule }}{\text { Coulomb } \times \text { Meter }}
$

The dimensional formula is $\left[M L T^{-3} A^{-1}\right]$

The electric field is a vector quantity and the positive charge is away from the charge and for the negative charge, it is towards the charge.

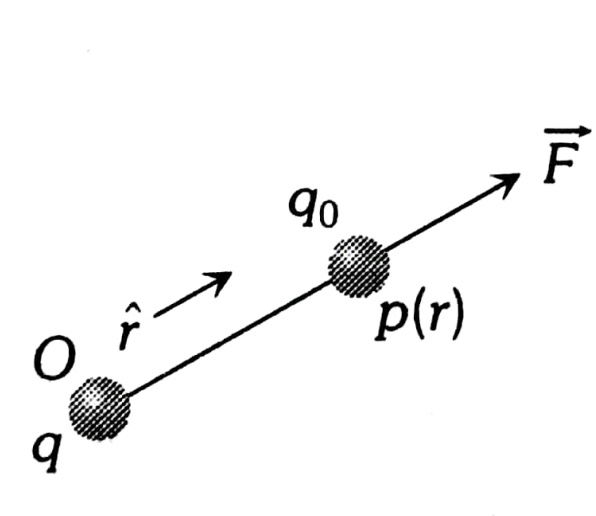
Electric field due to a point charge:

Consider a point charge placed at the origin O. Let a test charge q₀ is placed at P which is at a distance r from O. Force F on test charge q₀ is

$
F=\frac{1}{4 \pi \epsilon_0} \frac{q q_0}{r^2} \hat{r}
$

The electric field at point $P$ due to $q$ is

$
E=\lim _{q_0 \rightarrow 0} \frac{F}{q_0}=\lim _{q_0 \rightarrow 0} \frac{1}{q_0} \frac{1}{4 \pi \epsilon_0} \frac{q q_0}{r^2} \hat{r}=\frac{1}{4 \pi \epsilon_0} \frac{q}{r^2} \hat{r}
$

(As $\mathrm{q}_0$ tends to zero the electric field produced by q is not affected by $\mathrm{q}_0$.)
The magnitude of the electric field

$
E=\frac{1}{4 \pi \epsilon_0} \frac{q}{r^2}
$
Electric field due to a system of charge

The electric field obeys the superposition principle. That is the electric field due to a system of charge at a point is equal to the vector sum of all the electric fields.

Recommended Topic Video

Solved Examples Based on Electric Field

Example 1: The electric field inside a spherical shell of uniform surface charge density is

1) Zero

2) Constant, less than zero

3) Directly proportional to the distance from the centre

4) None of the above

Solution:

Electric Field

The space around a charge in which another charged particle experiences a force is said to have an electric field in it.

wherein

All charge resides on the outer surface so that according to Gauss's law, the electric field inside a shell is zero.

Example 2: If $E$ is the electric field intensity of an electrostatic field, then the electrostatic energy density is proportional to
1) $E$
2) $E^2$
3) $\frac{1}{E^2}$
4) $E^3$

Solution:

Electric Field

The space around a charge in which another charged particle experiences a force is said to have an electric field in it.

wherein

Electrostatic energy density $\frac{d U}{d V}=\frac{1}{2} K \varepsilon_0 E^2$

Hence, electrostatic energy density is proportional to $E^2$.

The correct option is (2).

Example 3: A combination of capacitors is set up as shown in the figure. The magnitude of the electric field, due to a point charge Q (having a charge equal to the sum of the charges on the 4 µF and 9 µF capacitors), at a point distant 30 m from it, would equal :

1) 240 N/C

2) 360 N/C

3) 420 N/C

4) 480 N/C

Solution:

Series Grouping

$\frac{1}{C_{\mathrm{eq}}}=\frac{1}{C_1}+\frac{1}{C_2}+\cdots$

wherein

Parallel Grouping

$C_{\mathrm{eq}}=C_1+C_2+\cdots$

wherein

Electric Field Intensity

$\vec{E}=\frac{\vec{F}}{q_0}=\frac{k Q}{r^2}$

wherein

$3 \mu F$ and $9 \mu F$ are in parallel combinations so their equivalent capacitance is

$
=3+9=12 \mu f
$

Now $4 \mu F$ and $12 \mu F$ are in series so their equivalent capacitance

$
=\frac{4 \times 12}{16}=3 \mu F
$
Charge on $3 \mu F=(3 \mu f) \times(8 V)=24 \mu C$
$\therefore$ Charge on $4 \mu F$ and $12 \mu F$ are same and it is $(24 \mu C)$ as they are in series

Charge on $9 \mu F=\frac{9}{9+3} \times 24 \mu F=18 \mu C$
Now required charge on $\mathrm{Q}=$ charge on $4 \mu F+$ charge on $9 \mu F$

$
\begin{gathered}
\therefore Q=[24+18] \mu C=42 \mu C \\
\therefore E=\frac{1}{4 \pi \epsilon_o} \frac{Q}{r^2} \Longrightarrow E=9 \times 10^9 \times \frac{42 \times 10^{-6}}{(30)^2}=420 N C^{-1}
\end{gathered}
$

Example 4: A thin semi-circular ring of radius $r$ has a positive charge $q$ distributed uniformly over it. The net field $\vec{E}$ at the centre $O$ is:

1) $\frac{q}{2 \pi^2 \varepsilon_0 r^2} \hat{j}$
2) $\frac{q}{4 \pi^2 \varepsilon_0 r^2} \hat{j}$
3) $-\frac{q}{4 \pi^2 \varepsilon_0 r^2} \hat{j}$
4) $-\frac{q}{2 \pi^2 \varepsilon_0 r^2} \hat{j}$

Solution:

Electric Field Intensity

$\vec{E}=\frac{\vec{F}}{q_0}=\frac{k Q}{r^2}$

wherein

$
\begin{aligned}
& \lambda=\frac{d q}{d l} \\
& d q=\lambda \cdot d l[d l=r d \theta] \\
& d E=\frac{1}{4 \pi r \varepsilon_0} \frac{d q}{r^2} \\
& =\frac{\lambda r d \theta}{4 \pi \varepsilon_o r^2}
\end{aligned}
$
The net electric field at $O$ is

$
\begin{aligned}
& E=\int_o^\pi d E \sin \theta(-\hat{j})=\int_o^\pi \frac{\lambda r d \theta}{4 \pi \varepsilon_o r^2} \sin \theta(-\hat{j}) \\
& E=-\int_o^\pi \frac{q r \sin \theta d \theta}{4 \pi^2 \varepsilon_o r^3} \hat{j} \\
& =-\frac{q}{4 \pi^2 \varepsilon_o r^2}(-\cos \theta)_o^\pi \hat{j} \\
& \therefore E=-\frac{q}{2 \pi \varepsilon_o r^2} \hat{j}
\end{aligned}
$

Example 5: The intensity of the electric field required to balance a proton of mass $1.7 \times 10^{-27} \mathrm{~kg}$ and charge $1.6 \times 10^{-19} \mathrm{C}$ is nearly
1) $1 \times 10^{-7} \mathrm{~V} / \mathrm{m}$
2) $1 \times 10^{-5} \mathrm{~V} / \mathrm{m}$
3) $1 \times 10^7 \mathrm{~V} / \mathrm{m}$
4) $1 \times 10^5 \mathrm{~V} / \mathrm{m}$Solution:

Electric Field Intensity

$\vec{E}=\frac{\vec{F}}{q_0}=\frac{k Q}{r^2}$

wherein

Since

$q E=m g$ or $E=\frac{m g}{q}=\frac{1.7 \times 10^{-27} \times 9.8}{1.6 \times 10^{-19}}$

After solving we get Ans A.

Summary

The electric field is a space around a charged particle which causes it to apply forces on other charged bodies. This is shown by lines that begin with positive charges and end with negative charges. Distance from the charge reduces the amount of field present. Understanding how electric forces function is highly dependent on electric fields which in turn influence the manner in which charged objects interact with one another.