Electromotive Force - Definition, Formula, Unit, Difference, FAQs

Edited By Team Careers360 | Updated on Nov 11, 2024 07:13 PM IST

What is Electromotive Force?

When an electric current is absent, the electromotive force is the voltage at the source's terminals. The phrase "electromotive force" refers to the amount of work required to separate the charge carriers in a source current in such a way that the force acting on the charges at the source's terminals is not a direct result of the field. Internal resistance leads to the development of emf.
EMF full form is electromotive force.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

What is Electromotive Force?
What is Electromotive Force Definition?
What is the unit of Electromotive Force?
Electromotive Force and Potential Difference:

Electromotive Force - Definition, Formula, Unit, Difference, FAQs

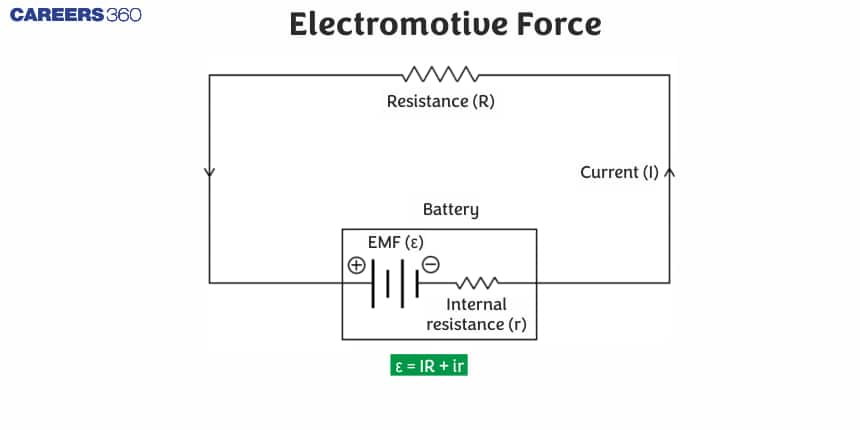
What is Electromotive Force Definition?

Emf Definition: The amount of work done in the energy transformation (or conversion) and the electricity that travels through the electrical source or generator is defined as the electromotive force (EMF). The electromotive force (EMF) symbol is ε and is measured in volts (or V). We will mostly address what is electromotive force, what is emf in physics, and what is the electromotive force formula? and other related topics in this article.

In physics, what is EMF?

Now we will know what EMF is in physics and what emf means in physics: When zero current is drawn from the cell, the electromotive force is the highest potential difference between the two electrodes. The Electromotive Force is represented by the letter E; however, it is also sometimes represented by the sign ε.

We know that charges move in an electric circuit; however, we must apply an external force to move the charges in a specific electric circuit. The electromotive force definition is that it is the force applied by the battery or an external electric source such as a battery to cause the charges to accelerate. It is not a form of force, despite its name, but rather a potential difference.

Also read -

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download E-book

What is the source of Emf?

Consider a basic circuit of a bulb connected to a battery to dispel these doubts.

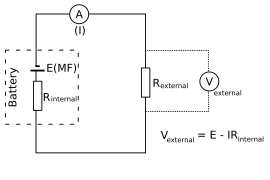
Internal resistance

Define Emf of a cell.

The battery (or any other electro-voltaic cell) can be thought of as a two-terminal device with one terminal at a higher potential than the other. The positive terminal, which has a higher electric potential, is sometimes referred to as the positive terminal and is usually denoted by a plus sign. The negative terminal, which is labelled with a minus sign, is the lower-potential terminal. This is referred to as the Electromotive force or emf source.

There is no flow of charges within the electromotive force source, when the source is separated from the light. Charges flow from one terminal to another, passing through the bulb after the battery is reconnected to the bulb. This causes the bulb to shine. Positive charges leave the positive terminal, pass through the lamp, and enter the negative terminal of the emf source in positive current flow, also known as conventional current flow. This is how you set up an emf source.

Now, what is electromotive force?

The potential difference created at both ends of a battery is the electromotive force of a cell.

Related Topics Link,

What is the unit of Electromotive Force?

What is the SI unit of electromotive force? Let's have a look at what the unit of electromotive force is. The electromotive force formula is as follows:

V+Ir=ε

Where,

The applied potential difference is denoted by the letter V.

I- The amount of current that flows through the circuit.

r- The circuit's internal resistance.

As a result, the volt is the unit of electromotive force. The electromotive force (EMF) is calculated by dividing the number of Joules of energy supplied by the source by each Coulomb required to carry a single electric charge across the circuit. In terms of math, it's as follows:

ε = Joules/Coulomb

As a result, the electromotive force's dimensions [M¹L²T^-³I^-1].

What's the difference between terminal voltage and electromotive force (EMF)?

EMF and terminal voltage differences are as follows:

The potential difference between the terminals of a load when the circuit is on is known as terminal voltage. EMF, on the other hand, is defined as the highest potential difference delivered by the battery while no current is flowing.

The terminal voltage is measured with a voltmeter, while the EMF is measured with a potentiometer.

Is it possible for the electromotive force to be negative?

Yes, there is a possibility that the electromotive force is negative. Consider the case of an inductor that generates an EMF that is in opposition to the incoming power. The resulting EMF is thus interpreted as negative because the flow direction is opposite to that of the true power. As a result, the electromotive force is possible to be negative.

Also Read:

Electromotive Force and Potential Difference:

Electromotive Force	Potential Difference
The work done on a unit charge is defined as EMF.	The energy dissipated when the unit charge passes through the components is defined as the potential difference.
The EMF does not change.	The difference in potential is not constant.
The EMF is unaffected by circuit resistance.	The resistance between the two points in a circuit during the measurement determines the potential difference.
E or ε is the symbol for it.	The potential difference symbol is V.

Electromotive Force, Terminal Voltage, and Internal Resistance Relationship

Potential Difference

The amount of work done in transporting a positive unit charge from one location to the other target point is described as the potential difference between two points in an electric circuit.

Work done is divided by the amount of charge transported equals the potential difference.

V=W/q

Here, the Potential Difference symbol is V

Example

When we state that the potential difference between two points is 3 volts, we mean that it takes 3 joules of energy to move a positive unit charge between them.

Terminal Voltage

Terminal voltage definition is when a current is supplied, the terminal voltage is the actual potential difference across the supply terminals.

Note:

When electrons move from negative to positive terminals in a closed circuit, the terminal voltage falls below the EMF value.

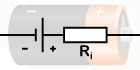
Internal Resistance

Chemical reactions within the cell can't keep up with the pace of charge separation to maintain maximal charge separation. Charges must flow between the electrolyte and the terminals, and there is always some internal resistance to this (r).

As a result, there is an internal voltage drop equal to Ir while current flows and the terminal voltage formula is given by V_T = ε - Ir.

Note that when current I=0, the terminal voltage is equal to ε.

Here is a representation of the voltage source and internal resistance for your better understanding.

Internal resistance model of a source of voltage

Also, check-

NCERT Physics Notes:

Frequently Asked Questions (FAQs)

1. What is the full form of EMF?

Full form of EMF is electromotive force.

2. What is the SI unit of EMF?

SI unit of emf is Joules/Coulomb

3. In terms of SI unit, J/Cis equal to which of the following quantity? A. Volt B. Pascal C. Omega D. Newton

Correct option is A.

4. An ideal voltmeter should have............to pass no current through it. A. Very large resistance B. Very small resistance C. Does not depend on resistance D. None of the above

Correct option is A.

5. A 44 Ω resistor is connected in series with a cell of internal resistance 4Ω and emf 12V. find the current flowing in the circuit.

IR = ε – Ir

I= R+r

I=1248

I = 0.25 A