Gauss Law Of Magnetism

Gauss's Law of Magnetism, one of Maxwell's equations, is a fundamental principle in electromagnetism that states that the net magnetic flux through any closed surface is zero. This law implies that magnetic monopoles do not exist; instead, magnetic field lines always form closed loops. In real life, this concept is evident in the behaviour of magnets. For example, if you break a bar magnet in half, each piece will still have both a north and a south pole, illustrating that magnetic monopoles cannot be isolated. Additionally, this principle is crucial in the design and functioning of various electromagnetic devices, such as electric motors and transformers, where the efficient routing of magnetic fields is essential for optimal performance. Understanding Gauss's Law of Magnetism helps in comprehending how magnetic fields interact with matter and how they can be harnessed in technology to perform useful work.

This Story also Contains

1. What is Magnetic Flux?
2. Gauss's Law of Magnetism
3. Solved Examples Based on Gauss Law of Magnetism
4. Summary

What is Magnetic Flux?

Magnetic flux is a measure of the quantity of magnetism, considering the strength and the extent of a magnetic field. It is defined as the product of the magnetic field (B) and the area (A) through which the field lines pass, and it also depends on the angle (θ) between the magnetic field and the normal (perpendicular) to the surface. It is defined as the magnetic lines of force passing normally through a surface called magnetic flux.

As we learn in electrostatic, the Gauss law for a closed surface states that

$\begin{aligned} & \phi_{\text {closed }}=\frac{q_{\text {net }}}{\epsilon_0} \\ & \text { where } \phi=\int \bar{E} d \bar{S} \\ & \end{aligned}$

S is the area enclosed and E is the electric field intensity passing through it.

and $q_{n e t}$ is the total charge inside the closed surface.

Gauss's Law of Magnetism

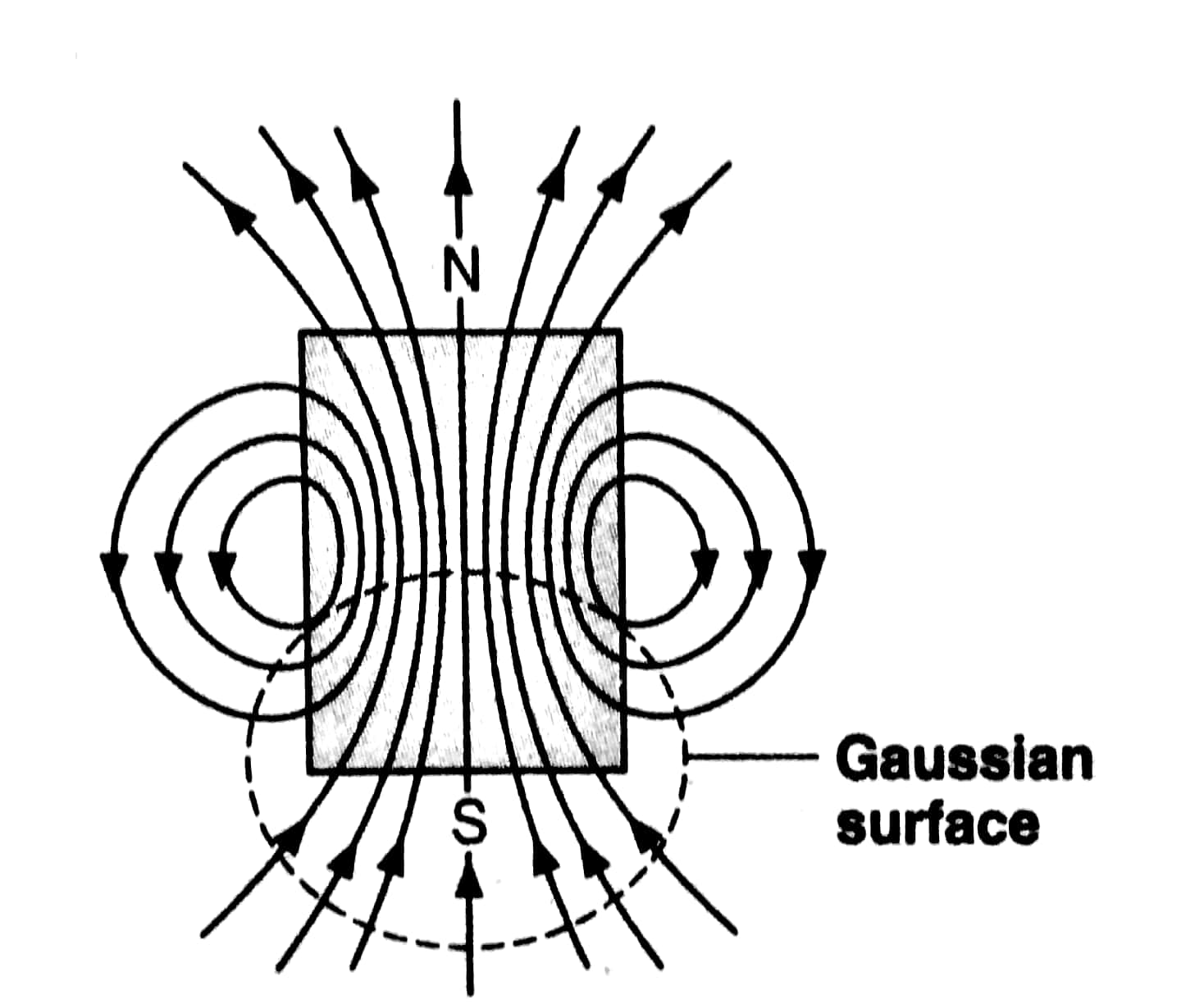
Gauss's Law of magnetism states that the flux of the magnetic field through any closed surface is zero (as shown in the below figure). It is because, inside the closed surface, the simplest magnetic element is a magnetic dipole with both poles (since a magnet with a monopole does not exist). So several magnetic field lines entering the surface equal the number of magnetic field lines leaving the surface. So the net magnetic flux through any closed surface is zero.

I.e Gauss law for a closed surface

$\oint \underset{B}{\rightarrow} \cdot \underset{d s}{\rightarrow}=0$

Gauss law if the surface is open

$\int \vec{B} \cdot \overrightarrow{d s}=\phi_B$

i.e. Consider an element of the area $d S$ on an arbitrarily shaped surface as shown in the figure. If the magnetic field at this element is $\vec{B}$, the magnetic flux through the element is $d \phi_B=\vec{B} \cdot d \vec{S}=B d S \cos \theta$

So, the total flux through the surface is

$\phi_B=\int \vec{B} \cdot d \vec{S}=\int B d S \cos \theta$

Recommended Topic Video

Solved Examples Based on Gauss Law of Magnetism

Example 1: Gauss law for magnetic field is given by

1) $\oint \vec{E} \cdot \overrightarrow{d s}=0$
2) $\oint \vec{B} \cdot \overrightarrow{d S}=0$
3) $E=-\frac{d \phi}{d t}$
4) $\oint \vec{B} \cdot \overrightarrow{d l}=\mu o I$

Solution:

Gauss's law in magnetism

Net magnetic flow through any closed surface is always zero.

wherein

$\oint \vec{B} \cdot \overrightarrow{d S}=0$

The divergence of magnetic flux density is zero, it implies the non-existence of magnetic monopoles in any magnetic field.

Hence, the answer is the option (2).

Example 2: Divergence theorem is based upon.

1) Gauss law

2) Stoke's law

3) Lenz law

4) Ampere's law

Solution:

Gauss law for a closed surface

$\oint \vec{B} \cdot \overrightarrow{d s}=0$

The divergence theorem relates surface integral and volume integral

and Gauss law works gives the relation between flux from a surface and magnetic pole enclosed in volume hence it can be a form of the divergence theorem.

Hence, the answer is the option (1).

Example 3: In a magnetic field of 0.05T, the area of the coil changes from $100 \mathrm{~cm}^2$ to $101 \mathrm{~cm}^2$ without changing resistance. Find out the change in flux.

1) $5 \times 10^{-5} \mathrm{wb}$
2) $5 \times 10^{-6} w b$
3) $4 \times 10^{-2} \mathrm{wb}$
4) $4 \times 10^{-6} w b$

Solution:

Gauss law if the surface is open

$\begin{aligned} & \int \underset{B}{\overrightarrow{d s}} \cdot \overrightarrow{d s} \\ & \Phi=\oint B \cdot d s \\ & \Phi_b=B \cdot \Delta A \\ & \Phi=0.05(101-100) \times 10^{-4} \\ & \Phi=5 \times 10^{-6} w b \\ & \end{aligned}$

Hence, the answer is the option (2).

Example 4: Curie temperature is the temperature above which

1) a ferromagnetic material becomes paramagnetic

2) a paramagnetic material becomes diamagnetic

3) a ferromagnetic material becomes diamagnetic

4) a paramagnetic material becomes ferromagnetic

Solution:

Curie Temperature or Curie Point

With the rise in temperature susceptibility of ferromagnetic materials decreases.

It is denoted by T_c

Curie Temperature is the temperature at which certain materials lose their permanent magnetic properties, to be replaced by induced magnetism.

A ferromagnetic material becomes paramagnetic above Curie temperature

Hence, the answer is the option (1).

Example 5: The magnetism of the magnet is due to

1) The spin motion electron

2) Earth

3) Pressure of big magnet inside the earth

4) cosmic rays

Solution:

Cause of magnetism

• The force exerted by the magnets when they attract or repel is known as Magnetism. This force is due to the motion of the electric charges.
• A strong magnetic force is produced when more electrons spin in the same direction. In every material, the magnetic field of the electron is void by contrasting a field of the magnet that is formed by the other pair of electrons.
• The magnetism property of the magnets depends on the materials and the direction of the spin of the electron.Hence the magnet’s magnetism is caused by the spin motion of the electrons

Hence, the answer is the option (1).

Summary

Gauss's Law of Magnetism, a fundamental principle in electromagnetism, asserts that the net magnetic flux through any closed surface is zero, indicating that magnetic monopoles do not exist and magnetic field lines always form closed loops. Magnetic flux, defined as the product of the magnetic field strength, area, and the cosine of the angle between them, measures the quantity of magnetism passing through a surface. Real-life examples include the behaviour of bar magnets, which demonstrate that breaking a magnet does not create isolated poles, and various electromagnetic devices where efficient magnetic field management is crucial.