Law of Conservation of Linear Momentum - Examples, FAQs

When two cars collide, the total momentum before and after the collision is the same, even though the cars may change speed or direction. This case can be better understood by studying the Law of Conservation of Linear Momentum in Physics. The below article will help us to understand the Law of Conservation of Linear Momentum with their examples in detail.

This Story also Contains

1. State the Law of Conservation of Linear Momentum
2. Law of Conservation of Momentum Derivation
3. Example of Law of Conservation of Linear Momentum
4. Solved Example Based on Conservation of Linear Momentum

State the Law of Conservation of Linear Momentum

The law of conservation of linear momentum works on the principle that when no external forces act on a system of two colliding objects, the vector sum of their linear momentum remains constant and is unaffected by their mutual interaction.

"The law of conservation of linear momentum states that if a system's net external force is zero, the system's total momentum remains constant."

S.I Unit of linear momentum is $\mathrm{kg} \cdot \mathrm{m} / \mathrm{s}$ and the direction of linear momentum remains the same as the direction of velocity.

Law of Conservation of Linear Momentum Formula

$$
\mathbf{p}=m \cdot \mathbf{v}
$$
Where:

• p: Linear momentum (vector quantity)
• $m$: Mass of the object (scalar quantity)
• v: Velocity of the object (vector quantity)

Characteristics of Linear Momentum

1. Linear momentum of a body is the quantity of motion contained in the body.

2. It is measured in terms of the force required to stop the body in a unit time.

3. If a body of mass $m$ is moving with velocity $\vec{v}$, then its linear momentum $\vec{p}$ is given by $\vec{p}=m \vec{v}$.

4. It is a vector quantity and its direction is the same as the direction of the velocity of the body.

5. S.I. Unit: kg-m/sec

6. Dimension $-\mathrm{MLT}^{-1}$

7. If two objects of different masses have the same momentum, the lighter body possesses greater velocity.

$\begin{aligned} & \text { As } \mathrm{p}=\mathrm{m}_1 \mathrm{v}_1=\mathrm{m}_2 \mathrm{v}_2=\text { constant } \\ & \therefore \frac{V_1}{V_2}=\frac{m_2}{m_1} \Rightarrow V \alpha \frac{1}{m}\end{aligned}$

Also read -

• NCERT Notes For All Subjects
• NCERT Solutions for All Subjects
• NCERT Exemplar Solutions for All Subjects

Law of Conservation of Momentum Derivation

When object A exerts a force on object B, object B reacts with a force of equal magnitude but in the opposite direction, according to Newton's Third Law of Motion

The principle of conservation of momentum is deduced from Newton's third law of motion

Consider two colliding particles A and B with masses of $m_1$ and $m_2$ with starting and ultimate velocities of $u_1$ and $v_1$ for A and $u_2$ and $v_2$ for B, respectively. The contact time between two particles is denoted by the letter t.

As shown in the figure:

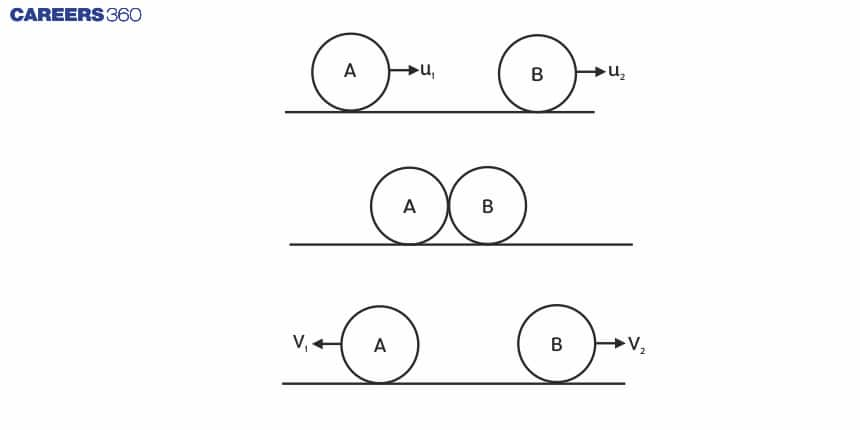
The change in the momentum of particle A is:

$
\Delta P_A = m_1 (v_1 - u_1)
$

The change in the momentum of particle B is:

$
\Delta P_B = m_2 (v_2 - u_2)
$

Using Newton's Third Law of Motion, we can write:

$
F_{BA} = -F_{AB}
$

Substituting for the forces:

$
F_{BA} = m_2 a_2 = \frac{m_2 (v_2 - u_2)}{t}
$

$
F_{AB} = m_1 a_1 = \frac{m_1 (v_1 - u_1)}{t}
$

Equating the two:

$
\frac{m_2 (v_2 - u_2)}{t} = -\frac{m_1 (v_1 - u_1)}{t}
$

Simplifying the equation:

$
m_1 u_1 + m_2 u_2 = m_1 v_1 + m_2 v_2
$

As a result, if no external force is exerted on the system, the momentum after the collision is equal to the momentum before the collision.

As a result, the equation of the law of conservation of momentum is as follows: $\mathrm{m}_1 \mathrm{u}_1+\mathrm{m}_2 \mathrm{u}_2$ represents the total momentum of particles A and B before the collision, and $\mathrm{m}_2 \mathrm{v}_2+\mathrm{m}_2 \mathrm{v}_2$ represents the total momentum of particles A and B after the collision.

Example of Law of Conservation of Linear Momentum

1. A Gun's Recoil: When a bullet is shot from a gun, both the bullet and the gun are initially at rest, with zero total momentum. When a bullet is fired, it accelerates forward. As a result of conservation momentum, the cannon acquires a backward momentum. A bullet with mass m is discharged at a forward velocity of v. The mass M gun achieves a rearward velocity u. The overall momentum before firing a bullet from the gun is zero, and the total momentum after firing is also zero.

2. Rocket propulsion involves a gas chamber at one end from which gas is expelled at high velocity. The total momentum is zero before the ejection. The rocket obtains a rebound velocity and acceleration in the opposite direction due to the ejection of gas. This occurs as a result of momentum conservation.

3. Motorboats: To conserve momentum, they push the water backward and forward.

These are some of the examples of the conservation of linear momentum that we see in our day-to-day lives. Now we will see some solved examples of the law of conservation of linear momentum.

Recommended Topic Video

Solved Example Based on Conservation of Linear Momentum

Question 1: An object of mass 1 kg travels at a constant speed of 10 m/s. Calculate the linear momentum (in kg-m/s )of the object.

(a) 10

(b) 40

(c) 30

(d) 15

Solution:

Given : Mass, $(m)=1 \mathrm{Kg}$

$ Speed (v)=10 \mathrm{~m} / \mathrm{sSo}$,

Linear momentum, $\vec{p}=m \vec{v}$

$
\vec{p}=m \vec{v} \Rightarrow \vec{p}=1 \mathrm{~kg} \times 10 \mathrm{~m} / \mathrm{s}=10 \mathrm{~kg} \mathrm{~m} / \mathrm{s}
$
Hence, the answer is option (a).

Question 2: If the speed and mass of an object are doubled, which of the following is true?

(a) The momentum of the object is doubled

(b) The momentum of the object is quadrupled.

(c) The momentum remains the same.

(d) The momentum is halved.

Solution:

Given :
Speed, $(v)=2 v$
Mass, $(m)=2 m$
We know,
Momentum, $(p)=m v$
According to the question if mass and speed are doubled. Then,

$
p=2 m \times 2 v=4 m v=4 p
$
Hence, the answer is option (b).

Question 3: A ball of mass 0.20 kg hits a wall at an angle of $45^{\circ}$ with a velocity of $25 \mathrm{~m} / \mathrm{s}$. Suppose the ball rebounds at $90^{\circ}$ to the direction of incidence with the same speed. Calculate the magnitude of change in momentum of the ball.

(a) $5 \sqrt{2} N s$

(b) 5 Ns

(c) $3 \sqrt{2} N s$

(d) 10 Ns

Solution:

Given-
mass, $\mathrm{m}=0.2 \mathrm{~kg}$
initial and final speed, $v=25 \mathrm{~m} / \mathrm{s}$
Magnitude of Initial linear momentum $\left(\vec{p}_i\right)$ and final linear momentum $\left(\overrightarrow{p_f}\right)-$

$
p=\left|\overrightarrow{p_f}\right|=\left|\overrightarrow{p_i}\right|=m v \Rightarrow p=5 \mathrm{~kg} \cdot \mathrm{m} / \mathrm{s}
$

Angle between initial and final momemtum vectors is $90^{\circ}$, as shown in the figure below-

Change in linear momentum-

$
\begin{aligned}
& \Delta \vec{p}=\overrightarrow{p_f}-\overrightarrow{p_i} \\
& |\Delta \vec{p}|=\left|\overrightarrow{p_f}-\overrightarrow{p_i}\right| \\
& |\Delta \vec{p}|=\sqrt{p^2+p^2-2 p^2 \cos 90^0} \\
& |\Delta \vec{p}|=\sqrt{2} p \\
& \Rightarrow|\Delta \vec{p}|=5 \sqrt{2} \mathrm{~kg} \cdot \mathrm{m} / \mathrm{s}
\end{aligned}
$
Hence, the answer is an option (a)

Question 4: An object is thrown vertically upwards. At its maximum height, which of the following quantities becomes zero?

(a) Momentum

(b) Potential Energy

(c) Acceleration

(d) Force

Solution:

At maximum height, its velocity becomes zero. Therefore, the momentum of the object becomes zero

The correct option is (1)

Question 5: A body of mass $M$ at rest explodes into three pieces, in the ratio of masses $1: 1: 2$. Two smaller pieces fly off perpendicular to each other with velocities of $30 \mathrm{~ms}^{-1}$ and $40 \mathrm{~ms}^{-1}$ respectively. The velocity of the third piece will be :

(a) $15 \mathrm{~ms}^{-1}$

(b) $25 \mathrm{~ms}^{-1}$

(c) $35 \mathrm{~ms}^{-1}$

(d) $5 \mathrm{~ms}^{-1}$

Solution:

Conservation of momentum,

$
\begin{aligned}
& \frac{\mathrm{m}}{4} \times 30 \mathrm{i}+\frac{\mathrm{m}}{4} 30 \mathrm{~J}+\frac{\mathrm{m}}{2} \overrightarrow{\mathrm{v}}=0 \\
& \tilde{\mathrm{v}}=-15 \mathrm{i}-20 \mathrm{~J} \\
& |\tilde{\mathrm{v}}|=\sqrt{15^2+20^2}=25 \mathrm{~m} / \mathrm{s}
\end{aligned}
$
Hence, the Correct answer is Option (b).