Maximum Length Of Hung Chain

When hanging a chain from the edge of a table, there is a critical point at which the chain will slip off due to gravity. Understanding the maximum length of the chain that can hang without falling is crucial for designing safe and effective suspension systems. This principle applies to various materials under tension, highlighting the importance of knowing their limits to ensure stability and safety.

This Story also Contains

1. What Is the Maximum Length Of Hung Chain?
2. Solved Example Based on Maximum Length Of Hung Chain
3. Summary

In this article, we will cover the concept of the Maximum Length Of a Hung Chain. This concept falls under the broader category of law of motion which is a crucial chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of two questions have been asked on this concept.

What Is the Maximum Length Of Hung Chain?

A uniform chain of length l is placed on the table in such a manner that its l' part is hanging over the edge of the table without sliding.

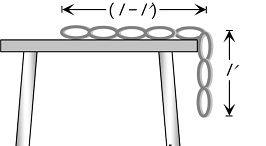
As,

$\mu=\frac{m_2}{m_1}=\frac{\text { mass hanging from table }}{\text { mass on table }}$

The chain will have uniform linear density.

So the ratio of mass and ratio of length for any part of the chain will be equal.

$\begin{aligned}
& \mu=\frac{\text { length of part hanging from table }}{\text { length of part on table }}=\frac{l^{\prime}}{l-l^{\prime}} \\
& l^{\prime}=\frac{\mu l}{(\mu+1)}
\end{aligned}$

Where the length of the chain
$
\begin{aligned}
& l^{\prime}=\text { chain hanging } \\
& \left(l-l^{\prime}\right)=\text { chain lying on the table }
\end{aligned}
$

After studying this concept, let's move to some solved examples to understand better.

Recommended Topic Video

Solved Example Based on Maximum Length Of Hung Chain

Example 1: A heavy uniform chain lies on a horizontal table top. If the coefficient of friction between the chain and the table surface is 0.25, then the maximum fraction of the length of the chain that can hang over one edge of the table is

1) 25%

2) 20%

3) 35%

4) 15%

Solution:

$\mu=\frac{m_2}{m_1}=\frac{\text { mass hanging from table }}{\text { mass on table }}$

The chain will have uniform linear density.

So the ratio of mass and ratio of length for any part of the chain will be equal.

$\begin{aligned}
& \mu=\frac{\text { length of part hanging from table }}{\text { length of part on table }}=\frac{l^{\prime}}{l-l^{\prime}} \\
& l^{\prime}=\frac{\mu l}{(\mu+1)}
\end{aligned}$

Where the length of the chain

$\begin{aligned}
& l^{\prime}=\text { chain hanging } \\
& \left(l-l^{\prime}\right)=\text { chain lying on the table }
\end{aligned}$

From the expression,

$\begin{aligned}
& l^{\prime}=\left(\frac{\mu}{\mu+1}\right) l=\left(\frac{0.25}{0.25+1}\right) l \quad[\text { As } \mu=0.25] \\
& \Rightarrow l^{\prime}=\frac{0.25}{1.25} l=\frac{1}{5}={ }_{20 \%} \text { of the length of the chain. }
\end{aligned}$

Hence, the answer is option (2).

Example 2 : The length of the chain is $L$ and the coefficient of static friction is $\mu$. Calculate the maximum length of the chain which can be hung from the table without sliding.

1) $\frac{\mu L}{1+\mu}$
2) $\frac{(\mu+1) L}{\mu}$
3) $\frac{\mu L}{1-\mu}$
(4) $\left(\frac{1-\mu}{\mu}\right) L$

Solution:

Let y be the maximum length of the chain that can be held outside the table without sliding

weight of the length of the chain on the table

$\begin{aligned}
& W^{\prime}=(L-y) \frac{M}{L} g \\
& \text { weight of hanging part of chain }=W=\frac{M}{L} y g
\end{aligned}$

For equilibrium:

limiting friction force = weight of hanging part of the chain

$\begin{aligned}
& F_L=\mu R=W \\
& \mu W^{\prime}=W \\
& \text { or } \mu \frac{M}{L}(L-y) g=\frac{M}{L} y g \\
& \mu L-\mu y=y \\
& y=\frac{\mu L}{1+\mu} \\
&
\end{aligned}$

Hence, the answer is option (1).

Example 3: A uniform chain of $6 \mathrm{~m}$ length is placed on a table such that a part of its length is hanging over the edge of the table. The system is at rest. The coefficient of static friction between the chain and the surface of the table is 0.5 , the maximum length of the chain hanging from the table is $\qquad$ ___ m.

1) 4

2) 1

3) 2

4) 2.5

Solution:

Let say. $\left(\frac{1}{n}\right)^{\text {th }}$ of chain length is hanging from the table
Mass of hanging length $=\mathrm{m}_1=\frac{\mathrm{m}}{\mathrm{n}}$
Mass of chain on table $=\mathrm{m}_2=\mathrm{m}\left(1-\frac{1}{\mathrm{n}}\right)$



At maximum hanging length,\begin{aligned}
& \mathrm{T}=\mathrm{f}=\frac{\mathrm{mg}}{\mathrm{n}} \\
& \mu\left(\mathrm{m}\left(1-\frac{1}{\mathrm{n}}\right) 9\right)=\frac{\mathrm{m} 9}{\mathrm{n}} \\
& 0.5\left(1-\frac{1}{\mathrm{n}}\right)=\frac{1}{\mathrm{n}} \\
& 1-\frac{1}{\mathrm{n}}=\frac{2}{\mathrm{n}} \\
& 1=\frac{3}{\mathrm{n}} \\
& \Rightarrow \mathrm{n}=3
\end{aligned}
Maximum Length of the chain hanging from the table
$
=\frac{1}{n}=\frac{6}{3}=2 \mathrm{~m}
$

Hence, the answer is option (3).

Example 4: A uniform metal chain of mass $m$ and length ${ }^{\prime} \mathrm{L}^{\prime}$ passes over a massless and frictionless pulley. It is released from rest with a part of its length $l$ is hanging on one side and the rest of its length hanging on the other side of the pully. At a certain point of time, when $l=\frac{L}{x}$, the acceleration of the chain is $\frac{g}{2}$. The value of $x$ is____. $\qquad$

1) 6

2) 2

3) 1.5

4) 4

Solution:

Let the mass of the complete chain be ' $\mathrm{m}$ 'and the mass of the chain of length $' \ell^{\prime}$ and ${ }^{\prime} \mathrm{L}-\ell^{\prime}$ be $\mathrm{m}_1$ and $\mathrm{m}_2$ respectively

$\begin{aligned}
& \mathrm{m}_1+\mathrm{m}_2=\mathrm{m} \\
& \mathrm{m}_1=\left(\frac{\mathrm{m}}{\mathrm{L}}\right) \ell \\
& \mathrm{m}_2=\left(\frac{\mathrm{m}}{\mathrm{L}}\right)(\mathrm{L}-\ell) \\
& \left(\mathrm{m}_2-\mathrm{m}_1\right)_{\mathrm{g}}=\left(\mathrm{m}_2+\mathrm{m}_1\right) \mathrm{a} \\
& \mathrm{a}=\left(\frac{\mathrm{m}_2-\mathrm{m}_1}{\mathrm{~m}_2+\mathrm{m}_1}\right) \mathrm{g} \\
& \frac{\mathrm{g}}{2}=\frac{\left(\frac{\mathrm{m}}{\mathrm{L}}\right)(\mathrm{L}-2 \ell)}{\mathrm{m}} \mathrm{g}
\end{aligned}$

$\begin{aligned}
& \frac{1}{2}=\frac{\mathrm{L}-2 \ell}{\mathrm{L}} \\
& \mathrm{L}=2 \mathrm{~L}-4 \ell \\
& 4 \ell=\mathrm{L} \\
& \ell=\frac{\mathrm{L}}{4} \\
& \therefore \mathrm{x}=4
\end{aligned}$

Hence, the answer is option (4).

Example 5: A uniform rope of length I lie on a table. If the coefficient of friction is $\mu$ then the maximum length $\mathrm{x}$ of the part of this rope which can overhang from the edge of the table without sliding down is :

1) l
2) $\frac{l}{\mu+1}$
3) $\frac{\mu l}{1+\mu}$
4) $\frac{\mu l}{1-\mu}$

Solution:

$
\frac{m_1}{m_2}=\frac{(l-x)}{x}
$

To prevent sliding
$
\begin{aligned}
& m_2 g=f=\mu m_1 g \\
& 1=\mu\left(\frac{l-x}{x}\right) \\
& \frac{1}{\mu}=\frac{l}{x}-1 \\
& \frac{1+\mu}{\mu}=\frac{l}{x}
\end{aligned}
$

$x=\frac{l(\mu)}{1+\mu}$

Hence, the answer is option (3).

Summary

This was essentially the article that evaluated the longest chain length that can be suspended from a certain surface without slipping away. We shared the view how friction comes right into play between the chain and the surface is because, absent it; the chain just slides right off. Anyhow, the article considered the calculation of the maximal length by taking into consideration the gravitational force acting on the chain as well as the opposing motion frictional force. In all these calculations the coefficient of friction and the weight of the chain play an important role.