Newtons Second Law of Motion and Momentum

Edited By Team Careers360 | Updated on Nov 11, 2024 07:24 PM IST

Linear Momentum

The scientific concept of linear momentum is similar to how most people perceive momentum: a large, fast-moving item has more momentum than a smaller, slower thing. The product of a system's mass times its velocity is defined as linear momentum. p = mv is the symbol for linear momentum.

The mass of an object, as well as its velocity, are directly proportional. As a result, the more mass or velocity an object has, the more momentum it has. The velocity v is accompanied by a vector called the momentum P. Momentum is measured in kilograms per second (kg m/s) in the SI system.

The concepts of force and momentum are closely connected. Force acting over time can affect momentum, thus Newton's second law of motion can be expressed in terms of momentum in its most general form. In quantum mechanics, momentum is still an important term in the study of atomic and subatomic particles.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

Linear Momentum
Newton's Second Law of Motion.
Newton's Second Law in terms of Momentum
The Second Law's Application

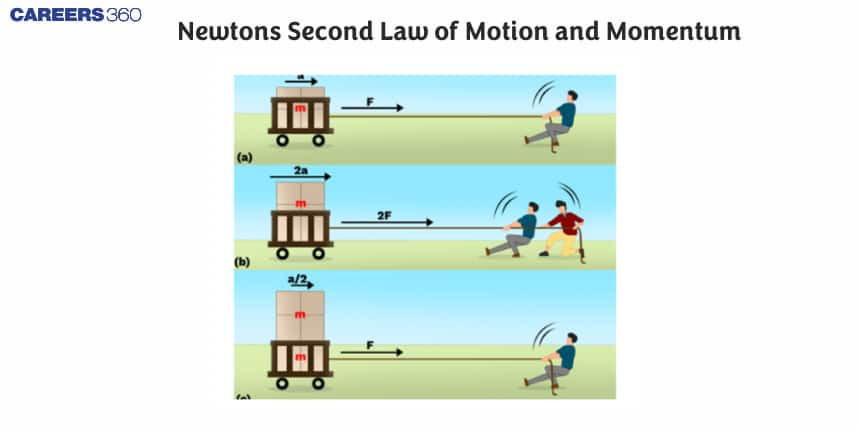
Newtons Second Law of Motion and Momentum

Also read -

Newton's Second Law of Motion.

The acceleration of an item is determined by two variables: the net force acting on it and the mass of the object, according to Newton's second law. Therefore, the body's acceleration is proportional to the body's net force and inversely proportional to its mass. This means that the acceleration of an object increases as the force acting on it increases. Similarly, when an object's mass grows, so does its acceleration.

The second law thus reduces to the more common mass-acceleration product:

F = ma

F = mass * acceleration

Keep in mind that this relationship is only valid for things with a fixed mass. This equation states that when an item is subjected to an external force, it will accelerate and that the quantity of acceleration is proportional to the force. The quantity of acceleration is also inversely related to the item's mass; given equal forces, a heavier object will experience less acceleration. A force causes a change in velocity, and a change in velocity produces a force, according to the momentum equation. It's a two-sided equation.

There is a magnitude and a direction associated with velocity, force, acceleration, and momentum. This is referred to as a vector quantity by scientists and mathematicians. The equations presented here are vector equations that can be used in any of the component directions.

NCERT Physics Notes:

Newton's Second Law in terms of Momentum

The net external force equals the change in momentum of a system divided by the time it changes, according to Newton's second law of motion. In equation form, this law is

F_net=dp/dt

Here, p is the momentum of the body.

Related Topics Link,

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download E-book

The Second Law's Application

The use of Newton's second law of motion can be observed in determining the amount of force required to move or stop an item. Here are a few examples to assist you grasp what we're talking about:

1. Slab of Bricks is broken by a karate player.

In order to smash a slab of bricks, a karate player employs Newton's second law of motion. Because the force is proportional to the acceleration, the player likes to move his or her hands quickly over the brick slab. This aids him in gaining speed and exerting a commensurate amount of power. The amount of force required to break the bricks is sufficient.

2. Kicking a soccer ball

We apply force in a precise direction when we kick a ball, which is the direction in which it will travel. Furthermore, the harder we kick the ball, the more force we apply to it, and the further it will travel.

Also read :

3. Object launched from a great height

When an object is hurled from a specific height, the earth's gravitational attraction aids acceleration. As the object approaches the Earth, its acceleration increases. Newton's second law of motion states that a body's acceleration is proportional to its force. When an object collides with the ground, the impact force is activated. This is why a brittle object thrown from a tall structure deforms more than one thrown from a lesser height.

4. Driving a vehicle

In simple terms, Newton's second law of motion asserts that any object with mass will produce an equivalent amount of acceleration if force is applied to it. When we turn on the ignition system of a car, for example, the engine creates enough force to allow the automobile to drive with proportionate acceleration.

5. A cart is being pushed.

In a supermarket, pushing an empty cart is easier than pushing one that is loaded. To accelerate, more mass requires more force.

6. Two individuals are walking.

If one of the two people walking is heavier than the other, the heavier person will walk more slowly since the lighter person's acceleration is greater.

Also check-

Frequently Asked Questions (FAQs)

1. When it comes to rockets, how does Newton's second rule of motion apply?

Force is a product of mass and acceleration, according to Newton's second law of motion. The force that is applied to the rocket is referred to as thrust. The acceleration will be larger as the thrust increases. The mass of the rocket also affects acceleration.

2. In an automobile accident, how does Newton's second law apply?

Force is defined as the dot product of mass and acceleration, according to Newton's second law of motion. In an automobile accident, the force is determined by the car's speed or acceleration. The force with which a car crash occurs increases as the acceleration or mass of the car increases.

3. What is Newton's second law's other name?

Newton's second law is sometimes also known as a law of force and acceleration.

4. What are some examples of Newton's second law of motion in everyday life?

Newton's second law of motion shows how force can modify an object's acceleration and how acceleration and mass are related in the same object. As a result, any change in an object's acceleration due to an applied force is an illustration of Newton's second law in everyday life.

The thrust provided to the rocket causes it to accelerate, which is an illustration of Newton's second law of motion.

The acceleration of an object falling from a specific height rises due to the gravitational force, which is another example of Newton's second law.

5. When it comes to sports, how does Newton's second law apply?

According to the second law of motion, force on an object is equal to its mass multiplied by its acceleration. When applied to a football, this law states that the amount of acceleration is determined by the quarterback's force and the mass of the ball.