Parallel Perpendicular Axes Theorem - Statement, Formula, FAQs

What is a Moment of Inertia?

We know that inertia is a property that a body already has, to resist the change in its linear state of motion or state of rest. This is a property that measures the mass of the body. However, the moment of inertia which is denoted by (I) is the measure of property or ability of a body to resist its state of rotational motion. It plays the same exact role in rotational motion as mass plays in linear motion and hence we can draw an analogy between them.

So, we can define the moment of inertia as the property of a body to oppose any change in its state of uniform motion or its state of rest $\mathrm{I}=\mathrm{Mr}^2$, where r is the perpendicular distance of a particle from the rotational axis and M is the mass of the body in rotational motion.

What is the Parallel Axis Theorem?

The moment of inertia of a body about an axis that passes through its centre is equal to the sum of that about an axis which passes through its centre, and the product of the mass of the body and the square of the distance between the two axes.

Parallel Axis Theorem Formula

The parallel axis theorem statement can be expressed as follows:

$
\mathrm{I}=\mathrm{I}_{\mathrm{C}}+\mathrm{Mh}^2
$
Where,

• I is the moment of inertia of the body
• $\mathrm{I}_{\mathrm{C}}$ is the moment of inertia about the center
• $M$ is the mass of the body
• $\mathrm{h}^2$ is the square of the distance between the two axes

Parallel Axis Theorem Derivation

Let $\mathrm{I}_{\mathrm{C}}$ be the moment of inertia of an axis that is passing through the centre of mass (AB from the figure) and I will be the moment of inertia about the axis $A^{\prime} B^{\prime}$ at a distance of $h$.

Consider a particle of mass $m$ at a distance $r$ from the centre of gravity of the body. Then,
Distance from $A^{\prime} B^{\prime}=r+h$

$
\begin{aligned}
& I=\sum m(r+h)^2 \\
& I=\sum m\left(r^2+h^2+2 r h\right) \\
& I=\sum m r^2+\sum m h^2+\sum 2 r h \\
& I=I_C+h 2 \sum m+2 h \sum m r \\
& I=I_C+M h^2+0 \\
& I=I_C+M h^2
\end{aligned}
$

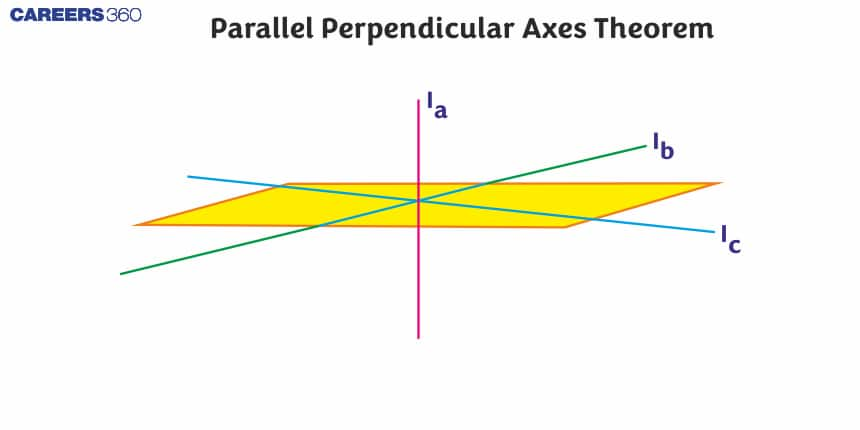
Perpendicular Axis Theorem

The perpendicular axis theorem states that for any plane body, the moment of inertia about any of its axes which are perpendicular to the plane is equal to the sum of the moment of inertia about any two perpendicular axes in the plane of the body which intersect the first axis in the plane.

Perpendicular Axis Theorem Formula

The perpendicular axis theorem is used when the body is symmetric in shape about two out of the three axes. If the moment of inertia about two of the axes is known the moment of inertia about the third axis can be found using the expression:

$
I_a=I_b+I_c
$

What is the application of parallel axis theorem?

Parallel Axis Theorem is used to find the moment of inertia of a body about any axis, when its moment of inertia about a parallel axis through its centre of mass is known.

Where it is used?
1. Calculating moment of inertia of complex bodies

Example: Moment of inertia of rods, discs, plates when the axis does not pass through their centre.
2. In engineering and mechanics

Used in designing beams, machine parts, flywheels, and rotating systems.
3. To shift axis of rotation

Helps when rotation is about an axis that is away from the center of mass.
4. In physics problems of rotational motion

Useful in solving questions of rolling bodies, compound pendulum, etc.

What is the Perpendicular Axis Theorem Used For?

Perpendicular Axis Theorem is used to find the moment of inertia of flat (planar) objects, when the object lies in a plane (usually the XY-plane).

Where it is used?
1. Finding moment of inertia along the $z$-axis If a lamina lies in XY-plane,

$$
I_z=I_x+I_y
$$

2. Used only for 2D bodies (lamina)

Example: discs, rings, rectangular plates, triangular plates, etc.
3. Useful in calculating MI of symmetric shapes

Helps in deriving formulas for moments of inertia of circles, rings, and polygons.
4. Common in problems of rotational motion

When rotation is perpendicular to the plane of the body.