Rigid Bodies Translational Motion and Rotational Motion

A rigid body shows two distinct types of motion that is translational and rotational motion. According to translational meaning , the movement which is uniform without any rotation. Translational motion in physics or what is translational motion can be defined in simple terms , such that when an extended rigid body traces a straight path it is in pure translational motion.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Rigid body
2. Translational motion
3. Rotational motion :
4. Difference between translational motion and rotational motion :

Rigid body

When a body has negligible or zero deformation , then it is known as rigid body. A rigid body is usually considered as a continuous distribution of mass . A perfect rigid body is when all the bodies are made up of atoms and molecules which are in a state of uniform motion . All the microscopic displacements are negligible and small , in this case the given body called rigid. In bengali rigid means দৃঢ়.

Also read -

• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 12 Physics
• NCERT Solutions for All Subjects

There are two types of rigid body motion

• Translational motion

• Rotational motion

Translational motion

Definition of translational motion :

When a body is moving in a straight line or a linear path , it is known as translational motion . In other words, translational motion is 1- dimensional motion .

Some translatory motion examples - motion of a box along a straight line , freely falling body .

Explanation of examples of translatory motion :

Translational motion of the box on a straight line

Translational motion of the box in an incline plane

• If a box is pushed in forward direction in straight path then its having a translational motion. When the box is pushed forward the whole body moves along with that each constituent particle of the that box also moves in forward direction. If we consider two particles as two points , then we can say the distance between two points is constant in this translational motion . Each particle will experience same effects as the box experiences.

• In a freely falling body ,when a body falls freely in downward direction . The distance between two constituent particle in the body is fixed. The motion of each particle in that body is similar to the translational motion of the whole body .

For translational motion , the coordinates of the body always stays in parallel to the space coordinate system , through the motion of a rigid body , the motion is called pure translational in nature. Due to translatory force a body move in a straight line with uniform motion. When the body moves from one point to the other in a straight path , this kind of movement is known as translational movement. The characteristic of a pure translational motion is that , during any time of interval ,every constituent particle of a rigid body undergoes the same amount of displacement. In translational motion rigid body behaves as a single particle . If , the motion of a particle in a rigid body can be described then the motion of the whole body can be described. If a body is fixed at one point it cannot have any translational motion. Translational motion meaning in hindi रैखिक गति .

NCERT Physics Notes:

• NCERT Notes Class 11th Physics
• NCERT Notes Class 12th Physics
• NCERT Notes For All Subjects

Types of translational motion :

1. Rectilinear motion

2. Curvilinear motion

The rectilinear motion is a part of translational motion .The main difference between rectilinear motion and translational motion is that the rectilinear motion denotes the motion only in a straight line where as translational motion means both types of motion when the object moves in straight path as well as in curved path .

Rotational motion :

When a body moves in a circular path about an axis , the motion is called rotational motion. The axis is called axis of rotation .

Example of rotational motion –motion of a wheel , motion of a ball.

Explanation of rotational motion :

Rotational motion of a wheel around its axis passing through centre

Also read :

• NCERT notes Class 11 Physics Chapter 7 System of Particles and Rotational motion
• NCERT solutions for Class 11 Physics Chapter 7 System of Particles and Rotational motion
• NCERT Exemplar Class 11 Physics Solutions Chapter 7 System of Particles and Rotational motion

When a wheel rotates around the axis passing normally through its centre then the motion is rotational motion .The whole body as well as the constituent particles of the wheel rotates along the axis .The wheel traces a circular path on its axis so it is a rotational motion.

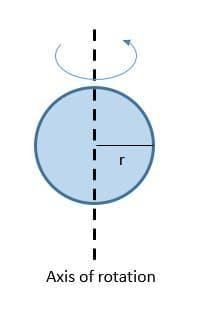
• The motion of a ball when it spins around its axis that passes normally through the centre of the ball then the ball and its constituent particles show rotational motion.

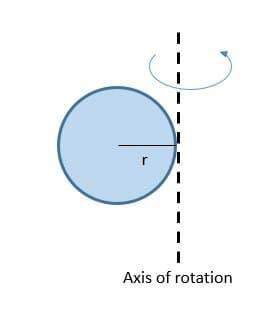
• In the same ball when the axis is shifted to the circumference then the whole ball will rotate around the axis . In this case also the ball traces a circular path. This is also rotational motion.

In pure rotational motion every constituent particles shows rotational motion along with the whole body .The rotation of a rigid body about a fixed axis , is known as axis of rotation .The pure rotation is that during any time interval ,every constituent particle of the rigid body experiences the same angular displacement. The whole rigid body behaves as a particle in case of pure rotation.

Difference between translational motion and rotational motion :

Also check-

• NCERT Exemplar Class 11th Physics Solutions
• NCERT Exemplar Class 12th Physics Solutions
• NCERT Exemplar Solutions for All Subjects