Relation Between Phase Difference and Path Difference

Relation Between Phase Difference and Path Difference - A Complete Guide

Edited By Vishal kumar | Updated on Sep 24, 2024 10:06 PM IST

Light is the electromagnetic wave and can travel through the vacuum. Vacuum meaning in Hindi is शून्य स्थान. These electromagnetic waves are categorized based on their wavelength or frequency. Wavelength of any electromagnetic wave is given by λ=c/f, where f is the frequency of the wave. Visible light occupies only a small part of the entire electromagnetic spectrum. Electromagnetic waves with shorter wavelengths and higher frequencies include ultraviolet rays, X-rays, and gamma rays. Long-wavelength, low-frequency electromagnetic waves include infrared, microwave, and broadcast television waves. Interference, in physics, the net effect of the combination of two or more wave trains moving on intersecting or coincident paths. Constructive interference happens when two waves are in phase so that their amplitudes are added to form the wave of more amplitude. Constructive meaning in Hindi is रचनात्मक. Constructive meaning in tamil is ஆக்கபூர்வமான(Ākkapūrvamāṉa)

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

Relation Between Phase Difference and Path Difference - A Complete Guide

The phase difference is the difference in phase angle of the two waves. Path difference is the difference in path of two waves. The meaning of path in Tamil is பாதை (patai). The relationship between phase difference and path deviation is simple. They are proportional to each other. ∅ is called the phase of the wave. The meaning of phase in English is to adjust something to harmonize it with something else. Phase meaning in physics is related to the angle at which waves travel. Phase difference between two waves ranges from 0 to 2π.

Also read -

For any two waves with the same frequency, Phase Difference and Path Difference are related as-

Phase difference formula or path difference formula

Δx= 2×∆∅

Where,

Δx is the path difference between the two waves.
Phase difference between two waves is represented by ∆∅

Above equation gives the relation between phase difference and path difference.

What is phase difference?

Phase difference can be defined as the variation of angle between any two waves or the particles having the same rate of frequency and starting from the same point. It is calculated in degrees or radians.

What is the path difference?

Path difference is the difference in path of two waves. Path of the wave can be expressed by its wavelength.

Related Topics Link,

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download E-book

Phase Difference And Path Difference Equation

The relation between the phase difference and phase angle can be given by the following expressions.

	Formula	Unit
The relation between phase difference and path difference	Δ∅/∆x= 2	No units
Phase Difference	Δ∅= 2×∆x	Radian or degree
Path Difference	Δx= 2×∆∅	meter

Phase Difference Waves

We define the phase difference of a sine wave as the length of time that one wave precedes or follows another. It should be noted that phase difference is not a property of a single wave, it is a property related to two or more waves.

We call the phase difference “Phase Shift” or “Phase Angle”. We represent the phase transition with the Greek letter Phi denoted ?.

The phase difference can be given by the following sine wave:

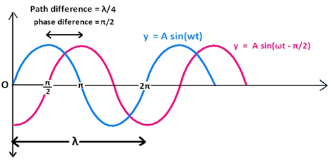Figure 1

Also Read:

Interference:

When two waves of equal wavelength intersect, they combine to form one wave. The resulting wave has the same wavelength as the two interacting waves, but its displacement at any point is equal to the algebraic sum of the displacements of the component waves (superposition principle). The formation of the resulting wave is due to the interference of two individual waves. Interference can be destructive or constructive depending on whether the movements are opposite or in the same direction. Structural interference is demonstrated using monochromatic (single wavelength/color) light, if the light waves combine to form waves of greater amplitude than the individual waves. As for light, the resulting wave will be brighter than the two individual waves. In the case of destructive interference, the amplitude of the resulting wave is smaller than the amplitude of the individual waves and will result in weaker light or no light at all (complete destructive interference).These waves are said to have coherence (the property that two waves of the same wavelength will maintain a constant phase relationship). This is why a laser (an instrument that generates intense, parallel beams of coherent light) is an excellent light source for this lab. When light from both slits hits a point on the screen, constructive or destructive interference occurs. As a result, a light or dark band (edge) will appear on the screen. See figure 2.

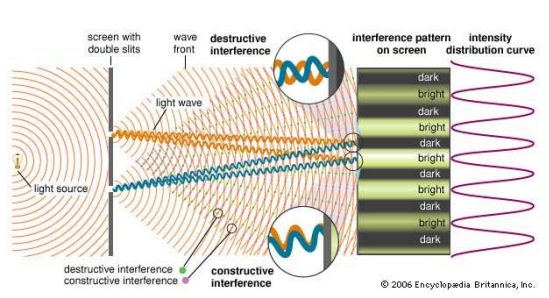Figure 2

When two light waves travel the same distance, they appear on a screen of the same phase and interfere with each other. Waves also interfere with each other (bright fringes) if the difference between the travel distances of each light source is equal to one full wavelength. However, if the difference in the distance the light travels is half a wavelength, then destructive will occur.

Diffraction:

Diffraction: Diffraction refers to the behavior of waves bending around obstacles or passing through small openings. Although light waves have the ability to diffract like other waves, they can be difficult to observe because of their very short wavelength [visible light band: λ (700 nm (red) > > 400 nm (violet)].

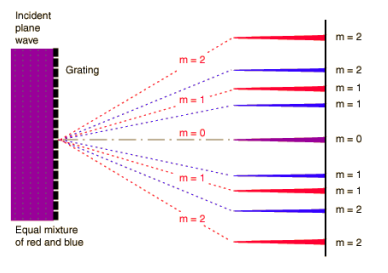$Diffraction$
Figure 3

The curvature of light as it passes through each of the two slits can be explained by Huygens Principle* (any point on the wavefront can be considered a wave source). Since each slit acts as a point light source, the light wave propagates from the slits and deviates from the line. Diffraction patterns are the result of constructive and destructive interference and therefore look like interference patterns. However, in the case of interference, the slits behave like point light sources, while for diffraction the true width of a single slit is taken into account. The amount of light that will bend is determined by the relative size of the light's wavelength relative to the size of the barrier or slit. If the aperture is much larger than the wavelength of light, the curvature will be nearly undetectable. However, if the size difference is small, the amount of light that will be bent will be small.

Also check-

NCERT Physics Notes:

Frequently Asked Questions (FAQs)

1. What is the relationship between phase difference and path?

The relationship between phase difference and path deviation is easy to understand. These two are proportional to each other. For any two waves of the same frequency, the phase difference and path difference are related because Δx is the path difference between the two waves, while ΔΦ is the phase difference between two consecutive waves.

2. What is phase difference in geometry?

If the frequencies are different, the phase difference increases linearly at time t. The phenomenon of cyclical change in the cyclic change of reinforcement and resistance is called dams.

3. What is the formula for the difference in paths?

If the distance traveled by the wave from two locations is the same, the path difference is zero. Once you know the path deviation, you can easily find the phase difference using the formula below: Here Δx is the path deviation and the phase difference.

4. What does the phase difference tell us?

We determine the phase difference (ϕ) between two particles or two waves which tells us how far a wave or particle is in front of or behind another wave or particle.