Unit of Wavelength - Definition, SI Unit, FAQs
Wavelength is the distance between two identical points of a wave, such as two consecutive crests, troughs, compressions or rarefactions. In physics, wavelength helps describe the size of a wave and how it behaves in different media. The SI unit of wavelength is the metre (m), and the symbol used for wavelength is λ (lambda). This article explains the unit of wavelength, its symbol, different units used for long and short waves, and a conversion table useful for Class 10, Class 11 and Class 12 students.
This Story also Contains
- What is Wavelength?
- What is the Unit of Wavelength?
- All Units of Wavelength
- Wavelength Units Used in Different Waves
- Relationship Between Wavelength and Frequency
- Example Problem - How to Calculate Wavelength

Also read
What is Wavelength?
Wavelength is the length of one complete wave cycle.
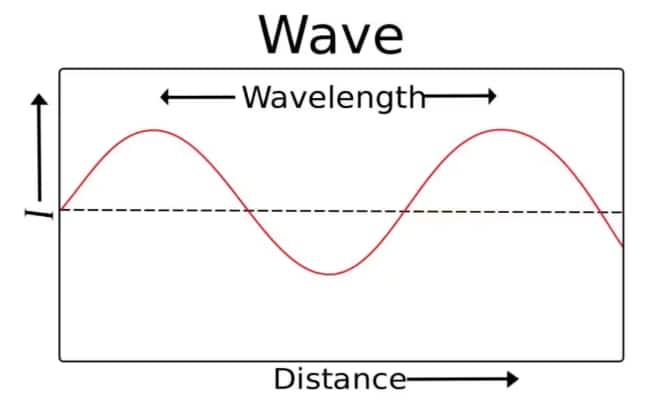
- In transverse waves, it is the distance between two crests or two troughs.
- In longitudinal waves, it is the distance between two compressions or two rarefactions.
Wavelength determines the colour of light, pitch of sound, and properties of electromagnetic waves.
What is the Unit of Wavelength?
SI Unit of Wavelength: Metre (m)
Since wavelength is a length, its SI unit is the same as that of any length:
$\text { Wavelength unit }=\text { metre }(\mathbf{m}) $
Symbol for Wavelength:
The symbol for wavelength is: $\lambda$
Dimensional Formula of Wavelength: $\left[M^0 L^1 T^0\right]$
Why Do We Use Different Units for Wavelength?
Wavelengths can be extremely long (radio waves) or extremely short (X-rays), so smaller or larger metric units are used depending on the wave type.
All Units of Wavelength
| Unit | Symbol | Value in Metres |
| Kilometre | km | $(10^3) $m |
| Metre (SI unit) | m | $(10^0)$ m |
| Decimetre | dm | $(10^{-1})$ m |
| Centimetre | cm | $(10^{-2}) $m |
| Millimetre | mm | $(10^{-3})$ m |
| Micrometre | μm | $(10^{-6}) $m |
| Nanometre | nm | $(10^{-9})$ m |
| Picometre | pm | $(10^{-12})$ m |
| Femtometre | fm | $(10^{-15})$ m |
| Megametre | Mm | $(10^6)$ m |
| Gigametre | Gm | $(10^9)$ m |
Wavelength Units Used in Different Waves
| Type of Wave | Typical Wavelength | Best Unit |
| Radio waves | km – m | km, m |
| Microwaves | cm – mm | cm, mm |
| Infrared | mm – μm | μm |
| Visible light | 400–700 nm | nm |
| Ultraviolet | 10–400 nm | nm |
| X-rays | 0.01–10 nm | nm |
| Gamma rays | < 0.01 nm | pm |
Relationship Between Wavelength and Frequency
The wavelength of a wave is related to its speed and frequency by:
$\lambda=\frac{v}{f}$
For light in vacuum:
$\lambda=\frac{c}{f}$
Where:
- $\lambda=$ wavelength
- $v$ or $c=$ speed of wave
- $f=$ frequency
Example Problem - How to Calculate Wavelength
Question: Find the wavelength of radiation whose frequency is $5 \times 10^{14} \mathrm{~Hz}$.
Solution:
$\lambda=\frac{c}{f}=\frac{3 \times 10^8}{5 \times 10^{14}}=6 \times 10^{-7} \mathrm{~m}$
or
$600 \mathrm{~nm}$
Summary
- Wavelength measures the length of one wave cycle.
- Symbol: $\lambda$
- SI Unit: metre (m)
- Smaller units: $\mathrm{nm}, \mu \mathrm{m}, \mathrm{pm}$
- Bigger units: $\mathrm{km}, \mathrm{Mm}$
- Shorter wavelength $\rightarrow$ higher frequency and energy
- EM waves have wavelengths from $10^{-12} \mathrm{~m}$ to $10^3 \mathrm{~m}$
Also check-
- NCERT Exemplar Class 11th Physics Solutions
- NCERT Exemplar Class 12th Physics Solutions
- NCERT Exemplar Solutions for All Subjects
NCERT Physics Notes:
Frequently Asked Questions (FAQs)
The wavelength will decrease.
λ=c/v =speed of light/frequency
= 3 X
Wavelength and frequency of a wave are inversely proportional. As wavelength increases, the frequency decreases.
Meters and Hertz are the SI unit of wavelength and frequency respectively.
The wavelength range of X-ray is 0.001-10 nm.
The wavelength of matter wave depends upon the mass, velocity, and momentum of the particle.
The red color has the longest wavelength of about 700 nm in the visible range.
The lower wavelength waves have the higher frequency and the higher energy as well, while the waves with higher wavelength hav the lower frequency and lower energy by the relation