Self Inductance

Self-inductance, a fundamental concept in electromagnetism, refers to the property of a coil or circuit that allows it to induce a voltage within itself when the current flowing through it changes. This phenomenon arises due to the magnetic field created by the current, which in turn influences the circuit's behaviour. In real life, self-inductance plays a crucial role in the functioning of various electrical devices. For instance, when you switch off a fluorescent light, the sudden interruption of current flow causes a rapid change in the magnetic field, inducing a voltage spike that can momentarily keep the light glowing. Similarly, in the ignition systems of cars, self-inductance is harnessed to generate the high-voltage sparks needed to ignite the fuel-air mixture in the engine. In this article, we will understand self-inductance is essential for designing efficient transformers, inductors, and many other components crucial to modern technology.

This Story also Contains

1. Inductance
2. Self Inductance
3. Faraday's Second Law of Induction EMF
4. Solved Examples Based on Self-Inductance
5. Summary

Inductance

Inductance, a fundamental property in the field of electromagnetism, measures a conductor's ability to store energy in its magnetic field when an electric current flows through it. It is a critical concept in the design and operation of electrical circuits and devices. Inductance is not just a theoretical concept but has practical applications in everyday life. For example, consider the charging cables used for smartphones

Self Inductance

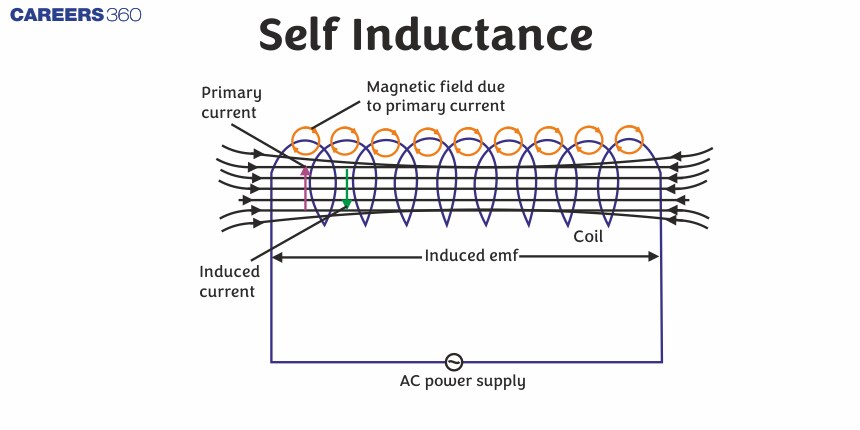
Self-inductance is a key principle in electromagnetism, describing a circuit element's ability to induce an electromotive force (EMF) within itself as a result of a changing current. When the current flowing through a coil or inductor changes, it alters the magnetic field around it, which in turn induces a voltage opposing the change in current. Whenever the electric current passing through a coil or circuit changes, the magnetic flux linked with it will also change. To oppose this flux change according to Faraday’s laws of electromagnetic induction, an emf is induced in the coil or the circuit. This phenomenon is called ‘self-induction’.

or

Self-inductance is defined as the induction of a voltage in a current-carrying wire when the current in the wire itself is changing. The emf induced is called back emf, and the current so produced in the coil is called induced current.

The direction of induced current for case A and case B is shown below.

Coefficient of Self-Induction

If $\phi$ is the flux linkages associated with 1 turn of the coil. And if N is the number of turns in the coil.

The total flux linkage associated with the coil is $N \phi$

And this total flux linkage is directly proportional to the current in the coil. i.e $N \phi \alpha i$

we can write $\phi_{\text {total }}=\phi_T=N \phi=L i$

where L= coefficient of self-induction.

So the coefficient of self-induction is given as $L=\frac{N \phi}{I}$

If $i=1 \mathrm{amp}, N=1$ then, $L=\phi$

i.e. The coefficient of self-induction of a coil is equal to the flux linked with the coil when the current in it is 1 amp.

Faraday's Second Law of Induction EMF

Using $\phi_{\text {total }}=N \phi=L i \quad$ and $\quad \varepsilon=\frac{-d \phi_T}{d t}$
we get
$
\varepsilon=-N \frac{d \phi}{d t}=-L \frac{d i}{d t}
$

If $\frac{d i}{d t}=1 \frac{a m p}{\sec }$ and $N=1$ then $|\varepsilon|=L$

i.e. The coefficient of self-induction is equal to the emf induced in the coil when the rate of change of current in the coil is unity.

Units and Dimensional Formula of ‘L’

S.I. Unit - Henry (H)

And $1 H=\frac{1 V \cdot s e c}{A m p}$

Its dimensional formula is $M L^2 T^{-2} A^{-2}$

Dependence of Self-Inductance (L)

It depends upon the number of turns (N), Area (A) and permeability of the medium $(\mu)$

‘L’ does not depend upon current flowing or change in current flowing.

Let us consider a long solenoid of N turns with length $l$ and area of cross-section $A=\pi r^2$. It carries current i as shown in the below figure.

Let n = number of turns per unit length $\frac{N}{L}$

whrere, N = total number of turns,

$l$ = length of the solenoid

If B is the magnetic field at any point inside the solenoid, then $B=\mu_0 n i$

The magnetic flux per turn = B × area of each turn

i.e Magnetic flux per turn $=\phi_0=\frac{\mu_o N i A}{l}$

So total flux is given as $\phi_T=N \phi_0=N * \frac{\mu_o N i A}{l}=\frac{\mu_o N^2 i A}{l} \ldots$

If $L$ is the coefficient of self-induction of the solenoid, then
$
\phi_T=\mathrm{Li} \ldots(2)
$

From equations (1) and (2)
$
\begin{aligned}
& \mathrm{Li}=\frac{\mu_{\mathrm{o}} \mathrm{N}^2 \mathrm{IA}}{l} \\
& \therefore \quad \mathrm{L}=\frac{\mu_{\mathrm{o}} \mathrm{N}^2 \mathrm{~A}}{l}
\end{aligned}
$

If the core is filled with a magnetic material of permeability $\mu$, then, $\mathrm{L}=\frac{\mu \mathrm{N}^2 \mathrm{~A}}{l}$

Recommended Topic Video

Solved Examples Based on Self-Inductance

Example 1: The total number of turns and cross-section area in a solenoid is fixed. However, its length $l$ is varied by adjusting the separation between windings. The inductance of solenoid will be proportional to :

1) $l$
2) $l^2$
3) $\frac{1}{l^2}$
4) $\frac{1}{l}$

Solution:

Inductance

It is the property of electrical circuits that oppose any change in the current in the circuits.

As we know :

Self-inductance, L

$
\begin{aligned}
\frac{L}{l} & =\mu_0 n^2 \pi r^2=\frac{\mu_0 N^2}{l^2} \pi r^2 \\
L & =\frac{\mu_0 N^2 \pi r^2}{l} \quad \text { (N,r is const. as given in question ) } \\
L & \propto \frac{1}{l}
\end{aligned}
$
( $\mathrm{N}, \mathrm{r}$ is const. as given in question)

Hence, the answer is the option (4).

Example 2: A coil of inductance 300 mH and resistance 2$\Omega$ is connected to a source of voltage 2 V. The current reaches half of its steady state value in

1) 0.15 s

2) 0.3 s

3) 0.05 s

4) 0.1 s

Solution:

Self Inductance

An emf is induced in the coil or the circuit which opposes the change that causes it. Which is also known as back emf.

wherein

During the growth of charge in an inductance,

$\begin{aligned} & I=I_0\left(1-e^{-R t / L}\right) \\ & \text { or } \frac{I_0}{2}=I_0\left(1-e^{-R t / L}\right) \\ & \text { or } e^{-R t / L}=\frac{1}{2}=2^{-1} \\ & \text { or } \frac{R t}{L}=1 n 2 \Rightarrow t=\frac{L}{R} 1 \mathrm{n} 2 \\ & t=\frac{300 \times 10^{-3}}{2} \times(0.693) \\ & \text { or } t=0.1 \text { sec }\end{aligned}$

Hence, the answer is the option (4).

Example 3: If a coil has 1 turn and 1 amp of current is flowing in a circuit, then the coefficient of self-induction would be, Where $\phi$ is the flux

1) $\phi$
2) $\phi_{/ 2}$
3) $\phi_{/ 4}$
4) $\phi_{/ 6}$

Solution:

The number of flux linkage with the coil is directly proportional to current i

$\begin{aligned} & N \phi \propto i \\ & N \phi=L i \\ & L=N \phi / i \\ & L=\phi\end{aligned}$

L is the coefficient of self-induction

Hence, the answer is the option (1).

Example 4: A wire of fixed length is wound on a solenoid of length '$l$' and radius '$r$'. Its self-inductance is found to be $L$. Now if the same wire is wound on a solenoid of length $\frac{l}{2}$ and radius $\frac{r}{2}$, then the self-inductance will be :

1) $2 L$
2) $L$
3) 4 L
4) $8 L$

Solution:

Coefficient of self-induction

$\begin{aligned} & \phi \alpha I \Rightarrow N \phi \alpha I \\ & N \phi=L I \\ & L=\frac{N \phi}{I}\end{aligned}$
wherein

$\begin{aligned} & N \phi=\text { The number of flux linkage with the coil. } \\ & L=\frac{\mu_0 N^2 \pi r^2}{l} \\ & \text { Length of wire }=N 2 \pi r=\text { Constant }(=C \text {, suppose }) \\ & \therefore L=\mu_0\left(\frac{C}{2 \pi r}\right)^2 \frac{\pi r^2}{l} \\ & \therefore L \propto \frac{1}{l}\end{aligned}$

$\therefore$ The inductance will become 2L

Hence, the answer is the option (1).

Example 5: What will happen to the inductance L of a solenoid when the number of turns and the length are doubled keeping the area of the cross-section the same?

1) $\frac{L}{2}$
2) $L$
3) 2 L
4) 4 L

Solution:

In the case of a solenoid as $\mathrm{B}=\mu_0 \mathrm{nI}$ $\phi=\mathrm{B}(\mathrm{n} / \mathrm{S})=\mu_0 \mathrm{n}^2 l \mathrm{SI}$ and hence $\mathrm{L}=\frac{\phi}{\mathrm{I}}=\mu_0 \mathrm{n}^2 l \mathrm{~S}=\mu_0 \frac{\mathrm{N}^2}{l} \mathrm{~S} \quad\left(\right.$ as $\left.\mathrm{n}=\frac{\mathrm{N}}{l}\right)$

When N and I are doubled, then
$
\mathrm{L}^{\prime}=\mu_0 \frac{(2 \mathrm{~N})^2}{2 l} \mathrm{~S}=2 \mu_0 \frac{\mathrm{N}^2}{l} \mathrm{~S}=2 \mathrm{~L}
$
i.e., the inductance of the solenoid will be doubled.
Hence, the answer is the option (3).

Summary

Self-inductance is a critical electromagnetism concept where a changing current in a coil induces a voltage within the same coil, opposing the change. This principle is crucial in various applications, such as car ignition systems and fluorescent lights. The coefficient of self-induction, denoted as L, depends on factors like the number of turns, area, and the medium's permeability, and it plays a vital role in the design and functioning of inductors, transformers, and other electrical components.