Sticking Of Person With The Wall Of Rotor
Have you ever seen an object fly off a spinning merry-go-round or tried to hold a book fixed on a rotating table? These everyday occurrences manifest rather interesting dynamics of objects on a rotating platform. Skidding-unfastening of objects- forwards and sideways- is both amusing and hazardous, depending on the situation. In this paper, we will be engaged in understanding the physics of objects skidding on moving platforms in the line of duty which involves friction, centripetal force, and inertia, among others. In furtherance to this, we will discuss some related practical implications such as how objects can be secured on a moving surface and what principle keeps rotating machines and amusement rides securely in place. In this article, we will cover the concept of Skidding of Object on a Rotating Platform. This concept falls under the broader category of laws of motion.
Skidding of Object on a Rotating Platform
Centrifugal force ≤ Force of friction mω2r≤μmg∴ωmax=μgr= It is the maximum angular velocity of rotation of the platform so that the object will not skid on it. ω= Angular velocity r= radius μ= coefficient of friction
Recommended Topic Video
Solved Examples Based on Sticking of Person With the Wall of Rotor
Example 1: As shown in the figure, a person of mass 'm' remains stuck to the wall of the rotating rotor. What should be the minimum value of angular velocity ω [coefficient of friction between wall and man is μ]

1) μgR
2) gR
3) gμR
4) μgR
Solution:
Sticking of Person with the wall of Rotor(Death well)

F= weight of person (mg)μR=mgμFc=mgμmωmin2r=mg∴ωmin=gμr Where F= friction force Fc= centrifugal force ωmin= minimum angular velocity μ= coefficient of friction r= radius of Rotor
From the figure

fr=mgμN=mg[fr=μN]μFc=mg[AsN=Fc]μmωmin2R=mg⇒ωmin=gμR
Hence, the answer is the option (3).
Example 2: A man is resting against the inner wall of a rotor which is moving with angular velocity ω. If the radius of the rotor is 2m and the coefficient of static friction between the wall and the person is 0.2. Find the minimum angular velocity (in rad/sec) for man to be at rest. (g= 10m/s2)
1) 5
2) 8
3) 10
4) 15
Solution
Sticking of Person with the wall of Rotor(Death well)
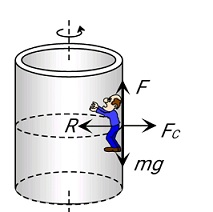
F = weight of person (mg)
μR=mgμFc=mgμmωmin2r=mg∴ωmin=gμr
wherein
F = friction force
Fc = centrifugal force
Wmin = minimum angular velocity
μ=coefficient of friction
r = radius of Rotor

N=mw2Rfs=μN=μmw2R
For the Resting position of the person
:fs=mg⇒μm2R=mgμω2R=gω2=gμR⇒100.2×2=25ω=5rad/sec
Hence, the answer is the option (1).
Example 3: A person stands in contact against the inner wall of a rotor of radius r. The coefficient of friction between the wall and the clothing is μ and the rotor is rotating about a vertical axis. What is the minimum angular speed of the rotor so that the person does not slip downward?
1) gμr
2) gμ
3) 2gμr
4) 1μr
Solution:
For the circular motion of the person
N=mrω2
Now for the vertical motion of the person
f=fmax=μNf=μmrω2
We also know f=mg
μmrω2=mgω=gμr
Hence, the answer is the option (1).
Example 4: A man of 50 pounds was made to stand against the inner wall of a hollow cylinder and the rotor of radius 5m is rotating at its vertical axis, and the coefficient of friction between the wall and his clothing is 0.35. What is the minimum angular speed of the rotor so that the person does not slip downward?
1) 2rads−1
2) 6rads−1
3) 5rads−1
4) 0.3rads−1
Solution:
The cylinder is in a vertical position. The normal reaction of the wall on man acts horizontally and it is equal to the centripetal force acting on it.
R=mrω2
Then the frictional force acts upward
F=mg
The man will still remain stuck to the wall after the floor is removed he will continue to rotate with the cylinder
μ≥FRF≤μRmg≤μmrω2ω2≤gμRω≤gμR
The minimum angular speed of rotation
ω=gμRμ=0.35,r=5 m,g=9.8 m/s2ω=9.80.35×5ω=2.31rads−1=2rads−1
Hence, the answer is the option (1).
Summary
Skidding on a rotating platform might happen since the frictional force between that object and the platform may not be sufficient to produce the needed centripetal force to keep it in its curved path. Because the platform rotates, the centripetal force pulls the object toward the centre. However, should the friction become too low because of a very smooth surface, large speed, or a heavy mass of the object, then the inertia of the object will just slide it outward. This very effect is what makes things slide off a lazy Susan and what keeps people safe on amusement park rides where they would skid if not for the safety features built into their ride. Something must be done in order to ensure adequate friction to keep things from skidding. Non-slip surfaces or proper tethering of objects will do the trick. Knowing these concepts a rotating platform or ride can be designed and run much safer from accident.