Gibbs energy change and Criteria for equilibrium

Gibbs free energy is also known as Gibbs function, Gibbs energy, or free energy. Gibbs free energy is a thermodynamic quantity. Gibb's free energy was discovered by an American scientist or physicist Josiah Willard Gibbs in the 1870s as a part of his work. His formulation of free energy and his contribution to statistical mechanics laid the principles for thermodynamics and chemistry.

This Story also Contains

1. Gibbs Energy Change
2. Some Solved Examples
3. Summary

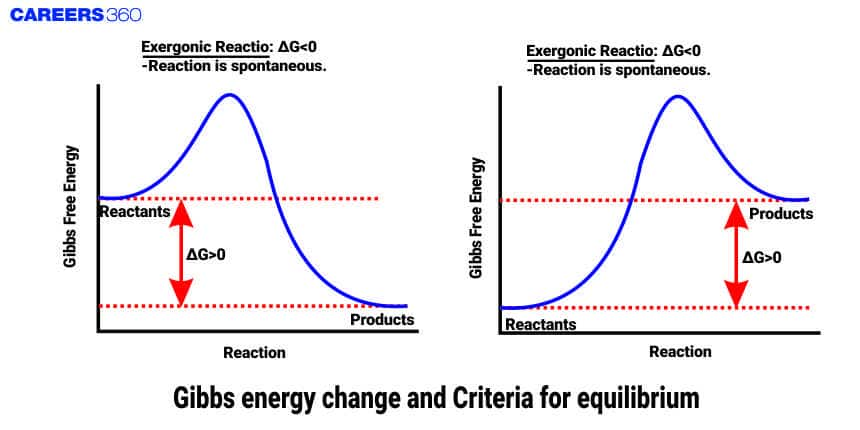
Gibbs free energy change is a state function and an extensive quantity that depends on the number or quantity of the substance. Gibbs free energy is the amount of energy that is available to do work. This energy is associated with the chemical reaction that can be used to work at constant temperature and pressure.

Gibbs Energy Change

It is a thermodynamic quantity that is used to predict the spontaneity of the reaction means whether the reaction can occur or not. It can only be concerned with changes in G values rather than its absolute value.

Mathematical Explanation Of Free Energy Change

It was introduced to relate H, and S and to explain spontaneity. According to J. Willard Gibb's Free energy of a system is defined as the maximum amount of energy available to a system during a process that can be converted into useful work.

or It is the thermodynamic quantity, especially characterizing the system, the decrease in whose value during a process is equal to the useful work done by the system.

It is denoted by G and it is given mathematically as follows:

$\mathrm{G}=\mathrm{H}-\mathrm{TS}$

Here,

H = Enthalpy

T = Absolute Temperature

S = Entropy

Also, we learned that

$\begin{aligned} & \mathrm{H}=\mathrm{E}+\mathrm{PV} \\ & \mathrm{G}=\mathrm{E}+\mathrm{PV}-\mathrm{TS}\end{aligned}$

Therefore, Free energy change at constant temperature and pressure is given as:

$
\Delta \mathrm{G}=\Delta \mathrm{E}+\mathrm{P} \Delta \mathrm{V}-\mathrm{T} \Delta \mathrm{S}
$

As $\Delta \mathrm{H}=\Delta \mathrm{E}+\mathrm{P} \Delta \mathrm{V}$
So, $\Delta \mathrm{G}=\Delta \mathrm{H}-\mathrm{T} \Delta \mathrm{S}$

At standard conditions that is, 298 K and 1 atm pressure

$\Delta \mathrm{G}^{\circ}=\Delta \mathrm{H}^{\circ}-\mathrm{T} \Delta \mathrm{S}^{\circ}$

It is called the Gibbs equation and it is used to explain the criterion of spontaneity, driving force, etc.

It is a state function and an extensive property.

Gibb's Free Energy Change for a Reaction

For a general reaction, it can be given as follows:

$\begin{aligned} & \mathrm{pA}+\mathrm{qB} \rightarrow \mathrm{rC}+\mathrm{sD} \\ & \Delta \mathrm{G}^{\circ}=\sum \Delta \mathrm{G}_{\mathrm{P}}^{\circ}-\sum \Delta \mathrm{G}_{\mathrm{R}}^{\circ} \\ & =\left[\left(\mathrm{r} \sum \mathrm{G}_{\mathrm{C}}^{\circ}+\mathrm{s} \sum \Delta \mathrm{G}_{\mathrm{D}}^{\circ}\right)-\left(\mathrm{p} \cdot \sum \Delta \mathrm{G}_{\mathrm{A}}^{\circ}+\mathrm{q} \sum \Delta \mathrm{G}_{\mathrm{B}}^{\circ}\right)\right]\end{aligned}$

This requires the exact same treatment as $\Delta \mathrm{H}$ or $\Delta \mathrm{S}$ or

Gibb's Free Energy Change for small changes in a Reversible process

$
\begin{aligned}
& \mathrm{G}=\mathrm{H}-\mathrm{TS} \\
& \mathrm{dG}=\mathrm{dH}-\mathrm{TdS}-\mathrm{SdT} \rightarrow(1)
\end{aligned}
$

Now,
$
\mathrm{dH}=\mathrm{dE}+\mathrm{PdV}+\mathrm{VdP} \rightarrow(2)
$

Using equations (1) and (2), we can write
$
\mathrm{dG}=\mathrm{dE}+\mathrm{PdV}+\mathrm{VdP}-\mathrm{TdS}-\mathrm{SdT} \rightarrow(3)
$

Now,
$
\mathrm{dE}=\mathrm{dq}+\mathrm{dw} ; \mathrm{dq}=\mathrm{TdS} ; \mathrm{dw}=-\mathrm{PdV}
$

Putting these values in the above expression (3), we have
$
\mathrm{dG}=\mathrm{VdP}-\mathrm{SdT}
$

Note: Remember this important formula for small changes in dG values

Recommended topic video on (Gibbs Energy Change And Criteria For Equilibrium)

Some Solved Examples

Example.1 The incorrect expression among the following is :

$
\text { 1) } \frac{\Delta \mathrm{G}_{\text {system }}}{\Delta \mathrm{S}_{\text {total }}}=-\mathrm{T}
$
2)isothermal process
$
\mathrm{W}_{\text {reversible }}=-\mathrm{nRT} \ln \frac{\mathrm{V}_{\mathrm{f}}}{\mathrm{V}_{\mathrm{i}}}
$
3) (correct) $\ln \mathrm{K}=\frac{\Delta \mathrm{H}^0-\mathrm{T} \Delta \mathrm{S}^0}{\mathrm{RT}}$
4) $K=e^{-\Delta G^0 / R T}$

Solution

As we learned,
$
\Delta \mathrm{G}^{\circ}=-\mathrm{RT} \ln \mathrm{K}
$
and $\Delta \mathrm{G}^{\circ}=\Delta \mathrm{H}^{\circ}-\mathrm{T} \Delta \mathrm{S}^{\circ}$
Thus, we can write
$
\begin{aligned}
& \Delta \mathrm{H}^{\circ}-\mathrm{T} \Delta \mathrm{S}^{\circ}=-\mathrm{RT} \ln \mathrm{K} \\
& \ln \mathrm{K}=-\left(\frac{\Delta \mathrm{H}^{\circ}-\mathrm{T} \Delta \mathrm{S}^{\circ}}{\mathrm{RT}}\right)
\end{aligned}
$

Hence, the answer is the option (3).

Example.2 For a particular reversible reaction at temperature $T, \Delta H$ and $\Delta S$ were found to be both +Ve.

If T_e is the temperature at equilibrium, the reaction would be spontaneous when-

$
\begin{aligned}
& \text { 1) } T=T_e \\
& \text { 2) } T_e>T
\end{aligned}
$
3) $\left(\right.$ correct) $T>T_e$
${ }_{4)} T_e$ is 5 times $T$

Solution

Gibb's free energy $(\Delta$ G)
$
\Delta G=\Delta H-T \Delta S
$

At equilibrium $\Delta G=0$
Hence, $\Delta G=\Delta H-T_e \Delta S=0$
$
\therefore \Delta H=T_e \cdot \Delta S \text { or } T_e=\frac{\Delta H}{\Delta S}
$

A spontaneous reaction $\Delta G$ must be negative which is possible only if $\Delta H<T \Delta S$

This will happen when T > T_e.

Hence, the answer is the option (3).

Example.3 Standard entropy of $\mathrm{X}_2, \mathrm{Y}_2$ and $\mathrm{XY}_3$ are 60, 40, and 50 J K^-1 mol^-1, respectively. For the reaction,

$\frac{1}{2} \mathrm{X}_2+\frac{3}{2} \mathrm{Y}_2 \rightarrow \mathrm{XY}_3, \Delta \mathrm{H}=-30 \mathrm{~kJ}$ to be at equilibrium, the temperature will be

1)1000 K

2)1250 K

3)500 K

4) (correct)750 K

Solution

For a reaction to be in equilibrium

$
\begin{aligned}
& \Delta \mathrm{G}=0 \\
& \Delta \mathrm{H}-\mathrm{T} \Delta \mathrm{S}=0 \\
& \therefore \Delta \mathrm{H}=\mathrm{T} \Delta \mathrm{S}
\end{aligned}
$

For reaction
$
\frac{1}{2} \mathrm{X}_2+\frac{3}{2} \mathrm{Y}_2 \rightarrow \mathrm{XY}_3, \Delta \mathrm{H}=-30 \mathrm{~kJ}
$

Calculating $\Delta S$ for the above equation, we get
$
\Delta \mathrm{S}=50-\left[\frac{1}{2} \times 60+\frac{3}{2} \times 40\right]=-40 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}
$

Thus at equilibrium,
$
\begin{aligned}
& \mathrm{T} \times(-40)=-30 \times 1000 \\
& \mathrm{~T}=\frac{-30 \times 1000}{-40}=750 \mathrm{~K}
\end{aligned}
$

Hence, the answer is the option (4).

Example.4 $\Delta_{\mathrm{f}} \mathrm{G}^0$at 500 K for substance ‘S’ in liquid state and gaseous state are +100.7 kcal mol −1 and +103 kcal mol⁻¹ , respectively. Vapour pressure (in atm) of liquid ‘S’ at 500 K is approximately equal to : (R=2 cal K⁻¹ mol⁻¹ ):

1) (correct)0.1

2)1

3)10

4)100

Solution

$\begin{aligned} & \Delta \mathrm{G} \text { of equilibrium } \\ & \Delta \mathrm{G}_0=-2.303 \mathrm{RT} \log \mathrm{K}_{\mathrm{c}} \\ & \text { At Equilibrium } \\ & \Delta G=0 \\ & \text { and } Q=K_{\mathrm{c}} \\ & \Delta \mathrm{G}_{\text {Reaction }}^{\mathrm{o}}=103-100.7=2.3 \mathrm{kcal}=2.3 \times 10^3 \mathrm{cal} \\ & \Delta \mathrm{G}^{\circ}=-2.303 \mathrm{RT} \log \mathrm{K}_{\mathrm{p}} \\ & 2.3 \times 10^3=-2.303 \times 2 \times 500 \log \mathrm{K}_{\mathrm{p}} \\ & \log \mathrm{K}_{\mathrm{p}}=-1 \\ & \mathrm{~K}_{\mathrm{p}}=10^{-1}=0.1 \mathrm{~atm}\end{aligned}$

Hence, the answer is an option (1).

Example. For the reaction

$\begin{aligned} & A(l) \rightarrow 2 B(\mathrm{~g}) \\ & \Delta U=2.1 \mathrm{kcal}, \Delta S=20 \mathrm{cal} \mathrm{K}^{-1} \text { at } 300 \mathrm{~K} \\ & \text { Hence } \Delta G \text { in } \mathrm{kcl} \text { is }----\end{aligned}$

1) (correct)-2.7 Kcal

2)3.3 Kcal

3)- 3.3 Kcal

4)2.7 Kcal

Solution

We know:
$
\begin{aligned}
\Delta \mathrm{G} & =\Delta \mathrm{H}-\mathrm{T} \Delta \mathrm{S} \\
\Delta \mathrm{H} & =\Delta \mathrm{U}+2 \mathrm{RT}
\end{aligned}
$

Thus, we have:
$
\Delta \mathrm{G}=\Delta \mathrm{U}+2 \mathrm{RT}-\mathrm{T} \Delta \mathrm{S}
$

On putting the given values we get:
$
\begin{aligned}
\Delta \mathrm{G} & =2.1+2 \times 2 \times 300 \times 10^{-3}-300 \times 20 \times 10^{-3} \\
\Delta \mathrm{G} & =2.1+4 \times 300 \times 10^{-3}-300 \times 20 \times 10^{-3} \\
\Delta \mathrm{G} & =1200 \times 10^{-3}-6000 \times 10^{-3} \\
\Delta \mathrm{G} & =2.1+1.2-6 \\
\Delta \mathrm{G} & =3.3-6 \\
\Delta \mathrm{G} & =-2.7 \mathrm{Kcal}
\end{aligned}
$

Hence, the answer is the option(1).

Summary

The spontaneity of the reaction is determined by the Gibbs free energy change. spontaneity means whether the reaction can occur or cannot occur. A reaction is said to be spontaneous when the value of free energy change is less than zero or negative. This indicates that the process can occur without the input of external energy. A reaction is said to be nonspontaneous when the value of free energy change is more than zero or positive. this means the reaction requires external energy to occur so that this reaction does not occur and when the value to free energy change is equal to zero the reaction is said to be in equilibrium