Area of Rectangle - Definition, Formula, Derivation and Examples

Edited By Team Careers360 | Updated on Jul 02, 2025 05:20 PM IST

A rectangle is a type of quadrilateral, a 2-D figure that has four sides and four vertices. In this article, we will learn how to calculate area of rectangle and its various applications in daily life, architecture, designing, etc. Rectangles are one of the most common geometric shapes in mathematics and found almost everywhere around us in the form of Books, windows, tables, laptops, tablets, etc.

This Story also Contains

What is Area of Rectangle?
Surface Area of Rectangle
Area of Rectangle Using Different Conditions
Solved Examples Based on Area of Rectangle

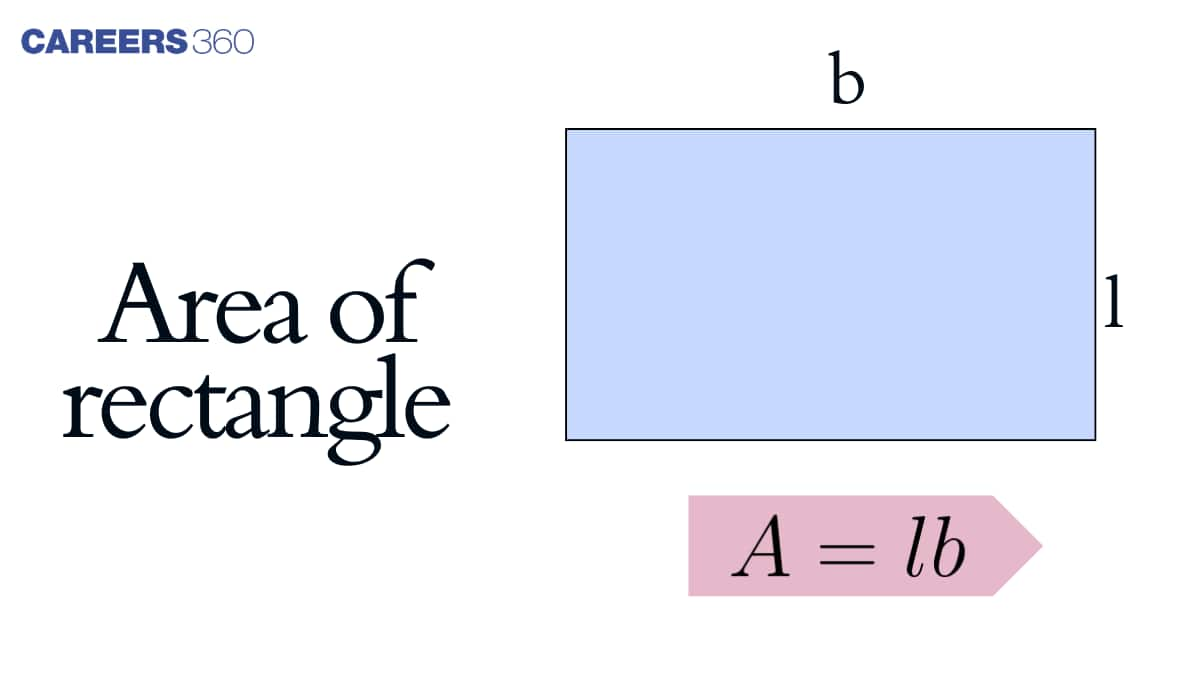
Area of Rectangle - Definition, Formula, Derivation and Examples

What is Area of Rectangle?

The area of rectangle can be defined as the region covered within the boundary of the rectangle. Or the other way round, the amount of surface covered by a rectangle is called the area of rectangle. When we talk about the other dimensions of figure, like angle, all the four angles of the rectangle are measured as 90 degrees with opposite sides being equal and parallel.

The area of a rectangle is dependent on its sides. The formula for area of rectangle can be stated as follows:

Area of rectangle is equal to the product of the length and breadth of the rectangle. Whereas when we speak about the perimeter, it is equal to the sum of all its four sides. Hence, we can conclude that the region within the perimeter of the rectangle is the area of rectangle.

Formula of Area of Rectangle

Area of rectangle = Length $\times$ Breadth

$
{A}={lb}
$

In the case of a square, the area will become ${side}^2$. The main difference between these two figures is that the length and breadth are equal for square.

Derivation of Area of Rectangle Formula

Consider the rectangle PQRS with a diagonal PR. Diagonal PR divides the rectangle PQRS into two congruent triangles. The area of rectangle PQRS is the sum of the area of these two triangles.

Area of Rectangle PQRS = Area of Triangle PQR + Area of Triangle PRS
Since both the triangles (PQR and PRS) are congruent, we can express it as follows.
Area of Rectangle PQRS $=2 \times$ Area of Triangle PQR
Area of Rectangle PQRS $=2 \times(\frac{1}{2} \times$ Base $\times$ Height $)$
Area of Rectangle PQRS $=2 \times \frac{1}{2} \times P Q \times Q R$
Area of Rectangle $P Q R S=P Q \times Q R$
Hence, Area of Rectangle $=$ Length $\times$ Breadth.

How to find Area of Rectangle?

Now, let's see how to find area of rectangle.

Step 1: We write down the dimensions of length and breadth from the data that is given to us in the question.

Step 2: Next, we multiply the length and breadth to calculate the area of rectangle.

Step 3: Finally we write the answer in square units like sq m, sq cm along with its magnitude.

Surface Area of Rectangle

Surface area of rectangle is defined as the area under the rectangle in an xy plane. We can use the following steps to find the surface area of the rectangle:

Step 1: First we multiply the length ($l$) by the width ($b$) of rectangle.

Step 2: Hence we come across the expression $l \times b$, where $l$ is the length and $b$ is the width of rectangle.

We can say that surface area of rectangle is same as that of area of rectangle.

Area of Rectangle Using Different Conditions

Area of rectangle using different conditions like area of rectangle using diagonal and area of rectangle using perimeter.

Area of Rectangle Using Diagonal

The area of a rectangle can be calculated if we know the diagonal and any one side of the rectangle. We initially define the diagonal of a rectangle as the straight line inside the rectangle connecting its opposite vertices. There are two diagonals in a rectangle and both of them are equal.

There are 2 ways we can approach this problem:

Method 1: Pythagoras theorem helps us to find the unknown side and then we find the area.

^{Example: Find area of rectangle whose length is 2 cm and whose diagonal is 3 cm .
Solution:
The breadth of the rectangle is missing and it can be calculated using the Pythagoras theorem because the diagonals of a rectangle form 2 right-angled triangles.}

^{In this case, the breadth can be calculated using the formula, breadth $=\left[\sqrt{(\text { Diagonal })^2-(\text { length })}^2\right]$}

^{After substituting the given values, we get}

^{$
\begin{aligned}
& \text { breadth }=\sqrt{(3)^2-(2)^2} \\
& \text {breadth }=\sqrt{9-4 } \\
& \text { breadth }=\sqrt{5 } =2.23 \mathrm{~cm}
\end{aligned}
$}

^{Now, we know that the length $=2 \mathrm{~cm}$, breadth $=2.23 \mathrm{~cm}$. So, the area of the rectangle $=l \times b$. In this case,}

^{$
A=l \times b
$}

^{Area $=2 \times 2.23=6.44 \mathrm{~cm}^2$}

Method 2:

Here we apply a direct method:

For example, missing part is the length of the rectangle where diagonal and breadth are known, then we write the length in terms of the breadth and diagonal and then use the formula for area.

We know that $(\text { Diagonal })^2=(\text { Length })^2+(\text { breadth })^2$. Or $(\text { Length })^2=(\text { Diagonal })^2-$ $(\text { breadth })^2$. Further, this can be expressed as, Length $=\sqrt{ }\left[(\text { Diagonal })^2-(\text { breadth })^2\right]$. Here, the length comes out in terms of the diagonal and breadth. This formula can be used in place of the length.

We know that the formula to calculate the area of rectangle is,

Area of rectangle $=$ Length $\times$ Width.

Hence, Area of rectangle $=\sqrt{ }\left[(\text { Diagonal })^2-(\text { breadth })^2\right]$ $\times$ Width.

So, Area of a Rectangle $=$ breadth $\sqrt{ }\left[(\text { Diagonal })^2-(\text { Width })^2\right]$.

Let us use an example to understand this.

Example: Find the area of rectangle in which the width is 5 units, and the diagonal is 9 units.

Solution:

We know the diagonal and the breadth of the rectangle. So, let us apply the direct formula, Area of Rectangle $=$ Width $\sqrt{ }\left[(\text { Diagonal })^2-(\text { Width })^2\right]$

After substituting the values of diagonal $=9$ units, and width $=5$ units, we get, Area of Rectangle $=$ Breadth $\sqrt{ }\left[(\text { Diagonal })^2-(\text { Width })^2\right]$

Area $=5 \sqrt{ }\left[(9)^2-(5)^2\right]$
Area $=5 \sqrt{ }(81-25)$
Area $=5 \times \sqrt{ } 56$
Area of rectangle $=37.4$ square units

Area of Rectangle Using Perimeter

With the help of perimeter, we can find the unknown side and then find area using the same formula, Area of rectangle formula $=$ Length $\times$ breadth.

Example: Find the area of rectangle if the perimeter is 20 units and the length is 6 units.

Solution:

Perimeter of the rectangle $=20$ units, length $=6$ units. We can find the breadth using the formula,

Perimeter of rectangle $=2(l+b)$
$20=2(6+b)$
$10=6+b$
$b=4$ units
breadth $=4$ units, length $=6$ units,
Area of rectangle $=1 \times b$
Area $=4 \times 6=24$ square units

Solved Examples Based on Area of Rectangle

Example 1: Find the area of rectangle whose length is 12 cm and the width is 2 cm.
Solution:
Given,
Length $=12 \mathrm{~cm}$
Width $=2 \mathrm{~cm}$
Area of rectangle formula $=$ Length $\times$ Width

$
12 \times 2=24
$

So the area of rectangle $=24 \mathrm{~cm}^2$

Example 2: What is the area of rectangular blackboard whose length and breadth are 200 cm and 100 cm, respectively.

Solution:
Length of the blackboard $=200 \mathrm{~cm}=2 \mathrm{~m}$
Breadth of the blackboard $=100 \mathrm{~cm}=1 \mathrm{~m}$
Area of the blackboard $=$ area of rectangle $=$ length x breadth $=2 \mathrm{~m} \times 1 \mathrm{~m}=2$ square-metres

Example 3: The length of a rectangular screen is 10 cm. Its area is $80 \mathrm{sq}. \mathrm{cm}$. Find its width.
Solution:
Area of the screen $=80 \mathrm{sq} . \mathrm{cm}$.
Length of the screen $=10 \mathrm{~cm}$
Area of rectangle formula $=$ length x width
So, width = $\frac{\text{area}}{\text{length}}$
Thus, width of the screen $=\frac{80}{10}=8 \mathrm{~cm}$

Example 4: The length and breadth of a rectangular wall are 70 m and 30 m, respectively. Find the cost of painting the wall if the rate of painting is Rs 3 per sq. m.

Solution:

Length of the wall $=70 \mathrm{~m}$
The breadth of the wall $=30 \mathrm{~m}$

Area of rectangle $=$ length $x$ breadth $=70 \mathrm{~m} \times 30 \mathrm{~m}=2100$ sq. m
For $1 \mathrm{sq}. \mathrm{m}$ of painting costs Rs 3
Thus, for 2400 sq. m, the cost of painting the wall will be $=3 \times 2100=$ Rs 6300

Example 5: A floor whose length and width is 60 m and 20 m respectively needs to be covered by rectangular tiles. The dimension of each tile is $1 \mathrm{~m} \times 2 \mathrm{~m}$. Find the total number of tiles that would be required to fully cover the floor.

Solution:
Length of the floor $=60 \mathrm{~m}$
The breadth of the floor $=20 \mathrm{~m}$
Area of the floor=area of rectangle $=$ length $\times$ breadth $=60 \mathrm{~m} \times 20 \mathrm{~m}=1200 \mathrm{sq} . \mathrm{m}$
Length of one tile $=2 \mathrm{~m}$
The breadth of one tile $=1 \mathrm{~m}$
Area of one tile $=$ length $x$ breadth $=2 \mathrm{~m} \times 1 \mathrm{~m}=2 \mathrm{sq} . \mathrm{m}$
No. of tiles required $= \frac{\text{area of floor}}{\text{area of a tile}}=\frac{1200}{2}=600$ tiles

List of Topics Related to Area of Rectangle

Area of Circle	Area of Isosceles Triangle
Area of Parallelogram	Area of Sphere
Area	Area of Quadrilateral
Area of Square	Area and Perimeter
Area of Equilateral Triangle	cm to inches converter

Frequently Asked Questions (FAQs)

1. What is the area of rectangle?

The area of rectangle is the space covered within the boundary of the rectangle. It is calculated by finding the product of the length and breadth (width) of the rectangle and is expressed in square units.

2. What is the perimeter and area of rectangle?

Perimeter is the sum of its four sides while area of rectangle the product of its length and breadth.

Formula for Perimeter of Rectangle = 2 (Length + Width).

Formula for Area of Rectangle = Length $\times$ Width.

3. What is the formula of area of rectangle?

The formula of area of a rectangle is the product of its length and width (breadth).
This is expressed as, Area of Rectangle $=$ length $\times$ width

4. What is the unit of area of rectangle?

The area of rectangle is expressed in square units. For example, if the dimensions of a rectangle are given in inches, then the area is expressed in square inches (in ${ }^2$ ). Similarly, if the dimensions are given in cm , then the area is expressed in square $\mathrm{cm}\left(\mathrm{cm}^2\right)$.

5. What is a rectangle?

It is a closed two-dimensional figure with four sides where opposite sides are equal and parallel to each other. The rectangle shape has all the angles equal to $90^{\circ}$.

6. What's the relationship between the area of a rectangle and the area of a triangle with the same base and height?

The area of a triangle is always half the area of a rectangle with the same base and height. This is because a rectangle can be divided into two equal triangles by drawing its diagonal.

7. What's the difference between the area of a rectangle and its diagonal length?

The area of a rectangle is a measure of its surface, while the diagonal is a linear measurement. The diagonal can be calculated using the Pythagorean theorem: diagonal² = length² + width². There's no direct relationship between area and diagonal length.

8. Can the area of a rectangle be used to solve real-world problems? Give an example.

Yes, the area of a rectangle is used in many real-world applications. For example, calculating the amount of carpet needed for a rectangular room, determining the output of a solar panel based on its dimensions, or figuring out how many tiles are needed to cover a rectangular floor.

9. Can you use the area of a rectangle to approximate the area of a circle?

Yes, you can approximate the area of a circle using rectangles. This is the basis of the method of exhaustion used in ancient mathematics. By inscribing or circumscribing many narrow rectangles around a circle, you can approximate its area. This idea is a precursor to integral calculus.

10. How does the concept of a rectangle's area apply in computer graphics and digital imaging?

In digital imaging, the area of a rectangle is crucial for understanding resolution. The number of pixels in an image is essentially the area of a rectangle. For instance, a 1920x1080 display has 2,073,600 pixels, which is the area of a rectangle with those dimensions.

11. Is the formula for the area of a rectangle the same as the formula for its perimeter?

No, the formulas are different. Area is calculated by length × width, while perimeter is calculated by 2(length + width). Area measures the space inside the rectangle, while perimeter measures the distance around it.

12. What's the difference between area and perimeter of a rectangle?

Area measures the space inside the rectangle (in square units), while perimeter measures the distance around the rectangle (in linear units). Area is calculated by length × width, while perimeter is calculated by 2(length + width).

13. Can two rectangles with different dimensions have the same area?

Yes, two rectangles with different dimensions can have the same area. For example, a rectangle with length 6 and width 4 has the same area (24 square units) as a rectangle with length 8 and width 3.

14. How can you use the area of a rectangle to find the area of more complex shapes?

Complex shapes can often be broken down into rectangles and other simple shapes. By calculating the areas of these component rectangles and adding them together (or subtracting if necessary), you can find the area of more complex shapes.

15. How does the area of a rectangle change if you increase one dimension and decrease the other by the same amount?

If you increase one dimension and decrease the other by the same amount, the area will decrease. For example, a 6x4 rectangle (area 24) changed to 7x3 (area 21) or 5x5 (area 25). This is due to the arithmetic mean-geometric mean inequality.

16. Why is the unit of area always squared (e.g., square meters, square feet)?

The unit of area is squared because area represents a two-dimensional measurement. It's the product of two linear measurements (length and width), so the units are multiplied as well. For example, 3 meters × 2 meters = 6 square meters.

17. Can a rectangle have an area of zero?

A rectangle can have an area of zero only if at least one of its dimensions (length or width) is zero. However, this would no longer be a true rectangle, but rather a line segment.

18. How is the area of a rectangle related to the concept of integration in calculus?

The area of a rectangle is a fundamental concept in integration. In calculus, the area under a curve is approximated by dividing it into many narrow rectangles and summing their areas. As the rectangles become infinitely narrow, this sum approaches the true area under the curve.

19. Can the area of a rectangle be expressed as a fraction?

Yes, the area of a rectangle can be expressed as a fraction. This often occurs when the length, width, or both are fractional. For example, a rectangle with length 1/2 and width 3/4 has an area of 3/8 square units.

20. How does the concept of scale factor apply to the area of rectangles?

When a rectangle is scaled by a factor k, its length and width are each multiplied by k. However, the area is multiplied by k². For example, if a rectangle's dimensions are doubled (k=2), its area increases by a factor of 2² = 4.

21. How is the area of a rectangle calculated?

The area of a rectangle is calculated by multiplying its length by its width. The formula is: Area = length × width (or A = l × w).

22. Why does multiplying length by width give us the area of a rectangle?

Multiplying length by width gives the area because it represents the number of unit squares that can fit inside the rectangle. The length determines how many squares fit in one row, and the width determines how many rows there are.

23. What happens to the area of a rectangle if you double its length but keep the width the same?

If you double the length of a rectangle while keeping the width constant, the area will double. This is because Area = length × width, so doubling one factor (length) will double the result (area).

24. How does the area of a rectangle change if both length and width are doubled?

If both length and width are doubled, the area of the rectangle increases by a factor of four. This is because (2l) × (2w) = 4(l × w), where l is the original length and w is the original width.

25. How do you find the length of a rectangle if you know its area and width?

To find the length of a rectangle when you know its area and width, divide the area by the width. This is derived from the area formula: Area = length × width, so length = Area ÷ width.

26. What's the difference between area and surface area when talking about rectangles?

Area typically refers to the space covered by one face of a rectangle (in 2D). Surface area is used for 3D objects and includes the total area of all faces. For a rectangular prism, you'd calculate the areas of all six rectangular faces and sum them.

27. How does the area of a rectangle relate to the concept of density in physics?

In physics, density is often calculated as mass per unit area for two-dimensional objects. For a rectangular sheet of material, you would divide its mass by its area to find its surface density. This concept is important in materials science and engineering.

28. How does the concept of a rectangle's area extend to three dimensions?

In three dimensions, the concept of a rectangle's area extends to the volume of a rectangular prism. Instead of length × width, we use length × width × height. The areas of the rectangle's faces become the surface areas of the prism's faces.

29. How does changing the units of measurement affect the calculated area of a rectangle?

Changing the units of measurement affects the numerical value of the area, but not the actual size of the space. For example, 1 square meter = 10,000 square centimeters. When converting, you must square the conversion factor.

30. How does the concept of a rectangle's area apply in computer programming?

In programming, especially in graphics and game development, rectangles are often used to define boundaries, collision detection, or screen layouts. The area calculation is used for determining overlap, scaling, and various other operations involving on-screen elements.

31. What is the definition of a rectangle?

A rectangle is a four-sided polygon (quadrilateral) with four right angles (90 degrees each). It has two pairs of parallel sides, with opposite sides being equal in length.

32. Can the area of a rectangle ever be negative?

No, the area of a rectangle (or any shape) can never be negative. Area represents physical space, which is always positive or zero. Even if length or width is expressed as a negative number, the result will be positive due to multiplication.

33. What's the difference between the area of a rectangle and its bounding box?

For a rectangle, its area and the area of its bounding box are the same thing. However, for other shapes, the bounding box is the smallest rectangle that can contain the shape, and its area is often larger than the area of the shape itself.

34. What's the relationship between the area of a rectangle and the concept of work in physics?

In physics, work is often represented graphically as the area under a force-displacement curve. When this curve is a horizontal line (constant force), the work done is equivalent to calculating the area of a rectangle, where force is the "height" and displacement is the "width".

35. What's the relationship between the area of a rectangle and its aspect ratio?

The aspect ratio of a rectangle is the ratio of its longer side to its shorter side. While the aspect ratio doesn't directly determine the area, it does describe the rectangle's shape. Two rectangles with the same area can have very different aspect ratios.

36. How does the golden ratio relate to rectangles?

The golden ratio (approximately 1.618:1) is considered aesthetically pleasing in rectangles. A "golden rectangle" has a length-to-width ratio equal to the golden ratio. While this doesn't affect the area calculation, it's an interesting geometric and artistic concept.

37. How is the concept of a rectangle's area used in probability and statistics?

In probability, the area of a rectangle often represents the probability of two independent events occurring together. In statistics, rectangles are used in histograms to represent data distribution, where the area of each rectangle is proportional to the frequency of data in that interval.

38. How does the concept of a rectangle's area apply in quantum mechanics?

In quantum mechanics, the area of a rectangle in phase space (with position on one axis and momentum on the other) represents a quantum of action. This is related to Heisenberg's uncertainty principle and the concept of quantization in quantum physics.

39. How does the concept of a rectangle's area apply in economics, particularly in supply and demand curves?

In economics, the area of a rectangle often represents economic surplus. For instance, in a supply-demand graph, consumer surplus is represented by the area of a "rectangle" (actually a triangle) above the price line and below the demand curve. Similarly, producer surplus is the area below the price line and above the supply curve.

40. Can the area of a rectangle be used to explain concepts in music theory?

Yes, in music theory, rectangles and their areas can be used to visualize and analyze rhythmic patterns. In a rhythmic grid, the width of a rectangle might represent duration, while its height could represent intensity or pitch. This type of visualization is often used in digital audio workstations and music composition software.

41. What's the relationship between the areas of similar rectangles?

The ratio of the areas of similar rectangles is equal to the square of the ratio of their corresponding sides. If one rectangle's sides are k times the sides of another, its area will be k² times the area of the other.

42. Can you have a rectangle with irrational dimensions? How would you calculate its area?

Yes, a rectangle can have irrational dimensions (like √2 or π). To calculate its area, you would still multiply length by width, but the result would be an irrational number. For example, a rectangle with sides √2 and √3 would have an area of √6 square units.

43. How does the area of a rectangle relate to the concept of definite integrals in calculus?

The area of a rectangle is a fundamental building block for understanding definite integrals. In calculus, the definite integral of a constant function over an interval is equivalent to calculating the area of a rectangle. This concept is then extended to more complex functions and curves.

44. Can the area of a rectangle be negative in any mathematical context?

While the physical area of a rectangle is always positive, in some mathematical contexts like vector spaces or when working with signed areas, a "negative area" can have meaning. For instance, when calculating the area of a polygon using the shoelace formula, individual terms can be negative.

45. What's the relationship between the area of a rectangle and the concept of flux in physics?

In physics, flux is often calculated as the product of a field strength and the area through which it passes. When this area is rectangular and the field is uniform, calculating flux is equivalent to calculating the area of a rectangle.

46. How does the concept of a rectangle's area relate to the idea of dimensional analysis?

Dimensional analysis is crucial in understanding area. The area of a rectangle has dimensions of length squared ([L]²). This helps in checking the consistency of physical equations and in converting between different unit systems.

47. Can the area of a rectangle be used to understand concepts in number theory?

Yes, the area of a rectangle can be used to visualize and understand concepts in number theory. For example, the fact that a×b = b×a (commutativity of multiplication) can be demonstrated by showing that a rectangle of length a and width b has the same area as a rectangle of length b and width a.

48. What's the relationship between the area of a rectangle and the concept of torque in physics?

While torque itself isn't an area, it can be represented graphically in a way that involves rectangular area. Torque is the product of force and lever arm length, which can be visualized as the area of a rectangle with force as height and lever arm as width.

49. How does the area of a rectangle relate to the concept of information theory and data compression?

In information theory, the area of a rectangle can represent the product of bandwidth and time, which is related to the amount of information that can be transmitted. In data compression, techniques like run-length encoding essentially compress data by representing repeated data as a "rectangle" with a width (run length) and height (data value).

50. Can the area of a rectangle be used to understand concepts in graph theory?

Yes, in graph theory, rectangles and their areas can be used to represent and analyze certain types of graphs. For example, in interval graphs, each vertex can be represented by an interval on a line, which can be visualized as a rectangle. The area of overlap between these rectangles can represent connections between vertices.

51. How does the concept of a rectangle's area apply in computer science, particularly in algorithm analysis?

In algorithm analysis, the area of a rectangle is often used to visualize time complexity. For example, in analyzing nested loops, the outer loop can be represented by the width of a rectangle and the inner loop by its height. The total number of operations (area) then represents the time complexity of the algorithm.

52. What's the relationship between the area of a rectangle and the concept of energy in physics?

In many physical scenarios, energy can be represented as the area of a rectangle. For instance, the energy stored in a capacitor is proportional to the area of a rectangle where voltage is one dimension and charge is the other. Similarly, in mechanics, the kinetic energy of an object can be represented as the area of a rectangle with mass as one dimension and the square of velocity as the other.

53. How can the area of a rectangle be used to understand concepts in linear algebra?

In linear algebra, the area of a rectangle can be used to visualize the determinant of a 2x2 matrix. If you plot the column vectors of a 2x2 matrix, the area of the parallelogram formed is equal to the absolute value of the determinant. This concept extends to higher dimensions as well.

54. How does the concept of a rectangle's area relate to the idea of cross-sections in multivariable calculus?

In multivariable calculus, the area of a rectangle is a fundamental concept in understanding cross-sections of three-dimensional objects. When you slice a 3D object with a plane, you often get a 2D shape. If this shape is rectangular, its area is crucial in techniques like the washer method or shell method for calculating volumes.

55. What's the relationship between the area of a rectangle and the concept of bandwidth in signal processing?

In signal processing, bandwidth is often represented visually as a rectangle in the frequency domain. The width of this rectangle represents the range of frequencies, while its height represents the signal strength. The area of this rectangle is related to the total power or information content of the signal within that frequency band.