Area Of Equilateral Triangle
Triangles are used in wide range of mathematics field and have many applications. Equilateral triangle is triangle whose sides are all equal. This article is about the concept of area of equilateral triangle. Let's see in detail what is area of equilateral triangle, various ways to find area of equilateral triangle formula with the help of parameters given to us like formula to find the area of equilateral triangle and area of equilateral triangle when height is given in this article.
This Story also Contains
- What is the Area of Equilateral Triangle?
- How to Find Area of Equilateral Triangle?
- Area of Equilateral Triangle in Different Conditions
- Solved Examples based on Area of Equilateral Triangle
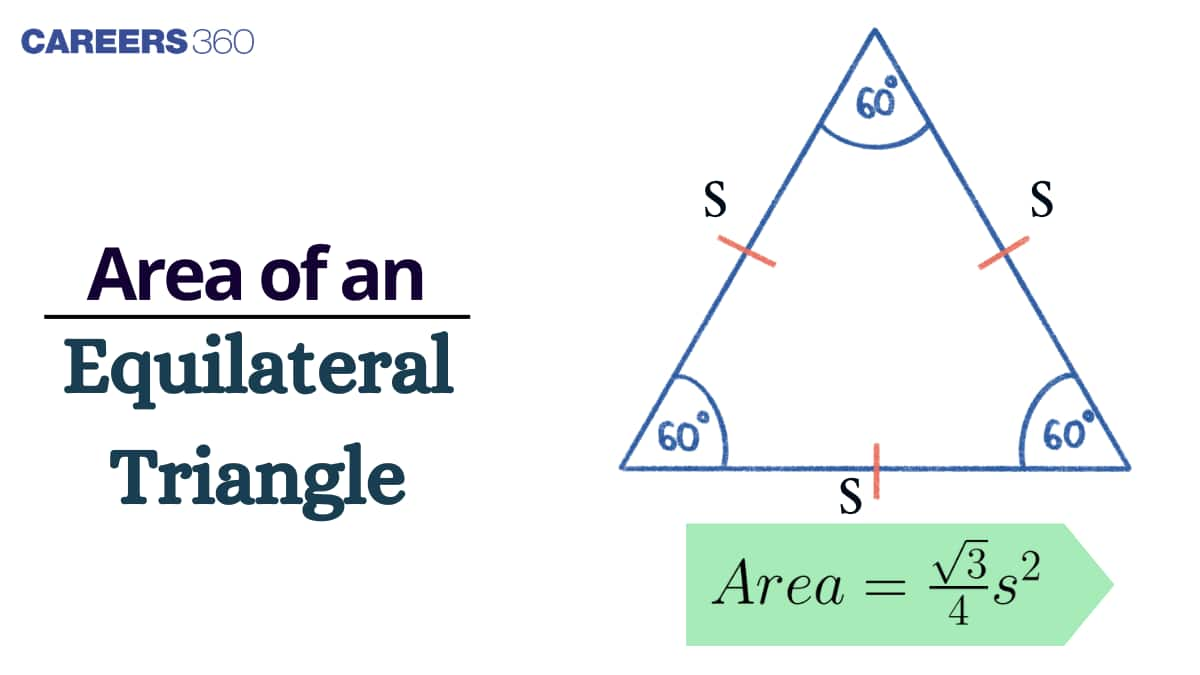
What is the Area of Equilateral Triangle?
In mathematics, we have 3 types of triangles, namely, equilateral triangle, isosceles triangle and scalene triangle. An equilateral triangle is a triangle which has all its sides equal in length. Also, each of its angles measures exactly 60 degrees. If we try to look for examples of such figure around us, we may find it in the form of parks or some buildings.
In general, area of equilateral triangle is the amount of space that an equilateral triangle covers in a 2-dimensional plane or the xy plane. SInce we know that area is always measured in units like sq m or sq cm, we use the same units to write the area of equilateral triangle. It is is a triangle with all sides equal and all its angles measuring $60^\circ$. According to the angle sum property of a triangle, the sum of all angles in an equilateral triangle is always $180^\circ$.
In geometry, area of equilateral triangle is defined as the region covered within three sides of the triangle and is expressed in square units like $\mathrm{in}^2, \mathrm{~m}^2, \mathrm{~cm}^2, \mathrm{yd}^2$, etc.
Formula of area of Equilateral triangle
The formula to calculate the area of equilateral triangle is given by: $=\frac{\sqrt{3}}{4} \times(\text { side })^2$
It is used to calculate the space within the sides of the equilateral triangle in a 2D plane. The area of figure becomes easy to calculate with formulas that involve less complex calculations. So it helps us to find out areas of buildings and figures which are in the shape of equilateral triangle which can be around us in various forms.
Area of Equilateral Triangle Formula Proof
To prove the area of equilateral triangle, consider an equilateral trianlge , adraw a altitude from one vertex to the midpoint of another. Now, the equilateral triangle is divided into two congruent triangles.
Now, as the base it divided into 2, the base of each triangle is $\frac{a}{2}$. We can note that the altitude is perpendicular to the base, so the 2 triangles formed are right angled triangle. No, let the altitude be $h$, hypotenuse be $a$ and the base is $\frac{a}{2}$.
By Pythagoreas Theorem,
$
h^2+\left(\frac{a}{2}\right)^2=a^2
$
$
\begin{gathered}
h^2+\frac{a^2}{4}=a^2 \\
h^2=a^2-\frac{a^2}{4} \\
h^2=\frac{4 a^2}{4}-\frac{a^2}{4} \\
h^2=\frac{3 a^2}{4} \\
h=\frac{\sqrt{3} a}{2}
\end{gathered}
$
Now, let us substitute the value of $h$ in the aea of triangle formula.
Area of Equilateral triangle $= \frac{1}{2} \times b \times h$ $\begin{gathered}=\frac{1}{2} \times a \times \frac{\sqrt{3} a}{2}=\frac{\sqrt{3} a^2}{4}\end{gathered}$
How to Find Area of Equilateral Triangle?
We use the following steps on how to find the area of equilateral triangle which makes the process very easy to understand and do the calculations:
Step 1: First we note the measure of the side length of the equilateral triangle that is given to us in the question.
Step 2: Next we apply the formula to calculate the equilateral triangle's area given as, Area of equilateral triangle $=\frac{\sqrt{3}}{4} a^2$ where, $a$ is the measure of the side length of the equilateral triangle.
Step 3: And then finally we express the answer with the appropriate units like sq m or sq cm.
Area of Equilateral Triangle in Different Conditions
The area of equilateral triangle with different conditions include area of equilateral triangle with height, area of equilateral triangle with 2 sides and included angle
Area of Equilateral Triangle with Height
In this case, we require the length of each side along with height. We will calculate the height of an equilateral triangle in terms of the side length. We follow the process of deriving equilateral triangle's area using area of triangle formula.

Area of equilateral triangle in terms of height is given is $\frac{1}{2} \times$ base $\times$ height
For finding the height of an equilateral triangle, we use the Pythagoras theorem.
Here, base $=\frac{a}{2}$, height $=\mathrm{h}$, hypotenuse $=\mathrm{a}$
Now, apply the Pythagoras theorem in the triangle.
$\begin{aligned}
& a^2=h^2+(\frac{a}{2})^2
& \Rightarrow h^2=a^2-\left(\frac{a^2}{4}\right)
& \Rightarrow h^2=\frac{\left(3 a^2\right)}{4}
\end{aligned}$
Or, $h=\frac{1}{2}(\sqrt{3 } a)$
Now, we substitute this value of ' $h$ ' in the area of the triangle equation.
Area of Triangle $=\frac{1}{2} \times$ base $\times$ height
$\Rightarrow A=\frac{1}{2} \times a \times \frac{1}{2}(\sqrt{3} a)$ [The base of the triangle is 'a' units]
Or, area of equilateral triangle $= \frac{1}{4} \left(\sqrt{3} a^2\right)$
Therefore, the area of equilateral triangle $= \frac{\sqrt{3}}{4} \times$ side $^2$
Area of Equilateral Triangle With 2 Sides and Included Angle (SAS)
Here comes in handy the application of the use of the sine trigonometric function to calculate the height of a equilateral triangle and use that value to find the area of the equilateral triangle.
Here we consider $a, b$, and $c$ are the different sides of a equilateral triangle.
When sides 'b' and 'c' and included angle $A$ is known, the area of the triangle is given by: $\frac{1}{2} \times bc \times \sin (A)$
When sides 'b' and 'a' and included angle $C$ is known, the area of the triangle is given by: $\frac{1}{2} \times ab \times \sin (C)$
When sides 'a' and 'c' and included angle $B$ is known, the area of the triangle is given by: $\frac{1}{2} \times ac \times \sin (B)$

In an equilateral triangle, $\angle A=\angle B=\angle C=60^{\circ}$. Therefore, $\sin A=\sin B=\sin C$. Now, area of $\triangle A B C=\frac{1}{2} \times b \times c \times \sin (A)=\frac{1}{2} \times a \times b \times \sin (C)=\frac{1}{2} \times a \times c \times \sin (B)$.
For an equilateral triangle, $\mathrm{a}=\mathrm{b}=\mathrm{c}$
Formula to find area of equilateral triangle $=\frac{1}{2} \times a \times a \times \sin (C)=\frac{1}{2} \times a^2 \times \sin \left(60^{\circ}\right)=\frac{1}{2} \times a^2 \times \frac{\sqrt{3}}{2}$
So, area of equilateral triangle $=(\frac{\sqrt{3}}{4}) \mathrm{a}^2$
Area of Equilateral triangle inscribed in a circle

Applying law of sine to the triangle $O B C$, we get
$
\frac{a}{\sin 60}=\frac{r}{\sin 30} \Rightarrow a=r \cdot \frac{\sin 60}{\sin 30} \Rightarrow a=\sqrt{3 } \cdot r
$
Now the area of the inscribed triangle is
$
A=\frac{1}{2} \cdot A M \cdot B C
$
Now $A M=A O+O M=r+r \cdot \sin 30=\frac{3}{2} \cdot r$
and $B C=a=\sqrt{3} \cdot r$
$A=\frac{1}{2} \cdot(\frac{3}{2} \cdot r) \cdot(\sqrt{3 } \cdot r)=\frac{1}{4} \cdot 3 \cdot \sqrt{3 } \cdot r^2$
Solved Examples based on Area of Equilateral Triangle
Example 1: Find the area of equilateral triangle of side 3 cm.
Solution:
The formula to find area of equilateral triangle is given by
Area of equilateral triangle $=\frac{\sqrt{3}}{4} \times(\text { Side })^2$
Formula to find area of equilateral triangle
$
\begin{aligned}
& =\frac{\sqrt{3}}{4} \times 3^2 \\
& =7.79 \text { inches }^2
\end{aligned}
$
Example 2: Calculate the area of equilateral triangle whose each side is $10 \mathrm{in}$.
Solution:
Given: Side = 10 in
Using the formula to find area of equilateral triangle,
Area $=\frac{\sqrt{3}}{4} \times(\text { Side })^2$
$
\begin{aligned}
& =\frac{\sqrt{3}}{4} \times(10)^2 \\
& =7.79 \text { inches } \mathrm{sq}
\end{aligned}
$
Example 3: How to find area of equilateral triangle with side 1 cm ?
Solution:
Given: Side $=1 \mathrm{~cm}$
formula to find area of equilateral triangle is given by,
$
\begin{aligned}
& \text { Area }=\frac{\sqrt{3}}{4} \times(\text { Side })^2 \\
& =\frac{\sqrt{3}}{4} \times(1)^2 \\
& =\frac{\sqrt{3}}{4} \mathrm{cm}^2
\end{aligned}
$
Therefore, the area of equilateral triangle is $0.86 \mathrm{~cm}^2$
Example 4: Find the area of equilateral triangle whose side is 4 cm.
Solution:
Given, side of the equilateral triangle $=\mathrm{a}=4 \mathrm{~cm}$
So, area of equilateral triangle $=\frac{\sqrt{ 3}}{ 4} a^2$
$
\begin{aligned}
& =(\frac{\sqrt{ 3}}{ 4}) \times 42 \mathrm{~cm}^2 \\
& =(\frac{\sqrt{ 3}}{ 4}) \times 16 \mathrm{~cm}^2 \\
& =13.85 \mathrm{~cm}^2
\end{aligned}
$
Example 5: What is area of equilateral triangle whose side is 20 cm?
Solution:
Given, side of the equilateral triangle $(a)=20 \mathrm{~cm}$
We know that, area of equilateral triangle $=\frac{\sqrt{3} a^2}{4}$
$
=346.4 \mathrm{~cm}^2
$
List of Topics Related to Area of Equilateral Triangle
| Area of Circle | Area of Isosceles Triangle |
| Area of Rectangle | Area of Sphere |
| Area | Area of Quadrilateral |
| Area of Square | Area and Perimeter |
| Area of Parallelogram | cm to inches converter |
Frequently Asked Questions (FAQs)
The area of an equilateral triangle is the region enclosed within the three sides of the equilateral triangle. It is expressed in square units.
The formula which is used to find the area of equilateral triangle is expressed as, Area of equilateral triangle $=\frac{\sqrt{3}}{4} \times (\text{side})^2$
All three sides should be equal, all three angles should be congruent and equal to 60 degrees. It is a regular polygon with three sides. The perpendicular drawn from vertex of the equilateral triangle to the opposite side bisects it into equal halves.
The perimeter of an equilateral triangle is the total length of its boundary which can be calculated using the formula, perimeter of an equilateral triangle = 3a, where 'a' is the side length.
Formula for area of equilateral triangle with height is expressed as, area of equilateral triangle $= \frac{\sqrt{3}}{4} \times \text{side}^2 $. And so if we know the height of an equilateral triangle, then the area can be calculated using this formula.
