Equation of Straight Line: Formula, Forms and Examples

Q: What is the equation of a line perpendicular to the given line?

Equation of line perpendicular to the given line. Let the given line be ax+by+c=0. The slope of the line is −a/b. Then the slope of the line parallel to the given line is −a/b Activate Windows

Q: How can you determine if three points are collinear using their coordinates?

Three points (x1, y1), (x2, y2), and (x3, y3) are collinear if the slope between any two pairs of points is the same. Alternatively, you can use the area of the triangle formed by these points; if it's zero, the points are collinear.

Q: How does the point-slope form of a line equation relate to its graph?

The point-slope form, y - y1 = m(x - x1), directly relates to a point (x1, y1) on the line and the slope m. It's useful when you know a point on the line and its slope, allowing you to easily generate other points.

Q: What is the significance of the distance formula in relation to line equations?

The distance formula, derived from the Pythagorean theorem, is used to find the distance between two points. It's crucial in deriving the point-slope form and in calculating the distance from a point to a line.

Q: How can you use the concept of a line to understand and solve differential equations?

Many first-order differential equations can be visualized as direction fields, where short line segments represent the slope at various points. The solutions to these equations are curves that are tangent to these line segments at each point.

Q: How does the slope-intercept form of a line differ from the general form?

The slope-intercept form is y = mx + b, where m is the slope and b is the y-intercept. It's a more specific version of the general form, explicitly showing the slope and y-intercept, making it easier to graph and interpret the line's behavior.

Equation of Straight Line: Formula, Forms and Examples

Edited By Komal Miglani | Updated on Jul 02, 2025 08:04 PM IST

We know that the equation of a straight line is linear in variables x and y. The general form of the equation of a straight line is ax+by+c=0, where a,b,c belongs to R and at least one of a and b is non-zero. We have different forms of the equation of straight lines depending upon through which point/points it is passing and in which direction it is drawn.

This Story also Contains

What is a Straight Line?
Equation of Straight Line in Slope-Intercept form
Derivation of Equation of Straight Line in Slope-Intercept form
Equation of Straight Line in Point-Slope form
Derivation of Equation of Straight Line in Point-Slope form
Equation of Straight Line in Two-point form
Derivation of Equation of Straight Line in Two-point form
Area of Triangle
Equation of Straight Line in Intercept form
Derivation of Equation of Straight Line in Intercept form
The normal form of a line
Derivation of the normal form of a line
The parametric form of a line
Derivation of the Parametric form of a line
Equation of line parallel to the x-axis
Equation of line parallel or perpendicular to the given line
Solved Examples Based on Equation of Straight Line
Summary

In this article, we will cover the concept of Equation of Straight Lines. This category falls under the broader category of Coordinate Geometry, which is a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. A total of seventeen questions have been asked on JEE MAINS( 2013 to 2023) from this topic including three in 2013, four in 2019, two in 2020, two in 2021, one in 2022, and one in 2023.

What is a Straight Line?

It is a curve such that all points on the line segment joining any two points on it lie on it.

Every equation of first degree in x , and y represents a straight line. The general equation of a straight line is given as ax+by+c=0 where a,b, and c are real numbers and at least one of a and b is non-zero.

Equation of Straight Line in Slope-Intercept form

The equation of the straight line in slope intercept form is given by y=mx+c

Derivation of Equation of Straight Line in Slope-Intercept form

Consider the given figure

AB is a straight line with slope m and intercept c on the Y-axis. P(x,y) is any point on the straight line. PL is perpendicular to X -axis and MQ is perpendicular to Y -axis
∠PRL=∠PQM=θ,OQ=cPM=PL−ML=PL−OQ=y−cQM=OL=x
In △PQM,tan⁡θ=PMQM=y−cx
tan⁡θ=m=y−cx⇒y=mx+c

The equation of a straight line whose slope is given as m and making y-intercept of length c unit is y=mx+c.
If the straight line passes through the origin, then the equation of the straight line becomes y=mx
If Equation of straight line is Ax+By+C=0, then
We can write By=−Ax−C
y=(−AB)x+(−CB)
compare with y=mx+c
slope =m=−ABy− intercept =c=−CB

Equation of Straight Line in Point-Slope form

The equation of a straight line whose slope is given as ' m ' and passes through the point (x1,y1) is y−y1=m(x−x1).

Derivation of Equation of Straight Line in Point-Slope form

Let the equation of give line I with slope ' m ' is
y=mx+c
(x1,y1) lies on the line i
y1=mx1+c

From (i) and (ii) [(ii) - (i)]
y−y1=m(x−x1)

The equation of a straight line whose slope is given as ' m ' and passes through the point (x1,y1) is y−y1=m(x−x1).

Equation of Straight Line in Two-point form

The equation of a straight line passing through the two given points (x1,y1) and (x2,y2) is given by
y−y1=(y2−y1x2−x1)(x−x1)

Derivation of Equation of Straight Line in Two-point form

Let the equation of straight line I with slope ' m ' be
y=mx+c

Points (x1,y1) and (x2,y2) pass through the given line I , then
y1=mx1+c
y2=mx2+c

Subtract eq (ii) from eq (i)
y−y1=m(x−x1)

Subtract eq (iii) from eq (i)
y−y2=m(x−x2)

Divide eq (iv) by eq ( v )
y−y1y2−y1=x−x1x2−x1⇒y−y1=(y2−y1x2−x1)(x−x1)
also here m=(y2−y1x2−x1)

Area of Triangle

If P(x,y),Q(x1,y1) and R(x2,y2) are collinear, then area of △PQR=0
i.e. 12|xy1x1y11x2y21||=0

Equation of Straight Line in Intercept form

The equation of a straight line which makes intercepts 'a' and 'b' on the X -axis and Y -axis respectively is given by
xa+yb=1

Derivation of Equation of Straight Line in Intercept form

A straight line that cuts the X -axis at A(a,0 ) and the Y -axis at B(0, b)
Using the concept of two points form a line
Equation of a straight line through the two-point A(a,0) and B(0,b)
y−0=b−00−a(x−a)⇒−ay=bx−ab⇒bx+ay=ab
divide LHS and RHS by ab
xa+yb=1

Note:
For the general equation Ax+By+C=0
If C≠0, then Ax+By+C=0 can be written as
Ax+By=−Cx−CA+y−CB=1 or xa+yb=1
where, a=−CA and b=−CB
Hence, the x-intercept is −CA and y-intercept is −CB.

The normal form of a line

The equation of a straight line on which the length of the perpendicular from the origin is p and this normal makes an angle θ with the positive direction of X-axis is given by
xcos⁡θ+ysin⁡θ=p

Derivation of the normal form of a line

AB is the straight line and the length of the perpendicular from the origin to the line is p (i.e. ON=p ).
Line AB cuts X-axis and Y-axis at points Q and R respectively

∠NOX=θ∠NQO=90∘−θ∴∠NQX=180∘−(90∘−θ)=90∘+θ Slope m=tan⁡(90∘+θ)=−cot⁡(θ) In triangle NOLOL=x= p. cos⁡θ,NL=y=p⋅sin⁡θ Point N( p.cos θ, p.sin θ)

Using Slope-point form, the equation of line AB is
y−p⋅sin⁡θ=−cos⁡θsin⁡θ(x−p⋅cos⁡θ)x⋅cos⁡θ+y⋅sin⁡θ=p

The parametric form of a line

The equation of a straight line passing through the point (x1,y1) and making an angle θ with the positive direction of the X-axis is
x−x1cos⁡θ=y−y1sin⁡θ=r

where r is the directed distance between the points (x,y) and (x1,y1).

Derivation of the Parametric form of a line

AB is a straight line passing through the point P(x1,y1) that meets the X-axis at R and makes an angle θ with the positive direction of the X-axis.

Let Q(x,y) be any point on the line AB at a distance ' r ' from P
As from the figure
PN=ML=OL−OM=x−x1QN=QL−NL=QL−PM=y−y1 In ΔNPQcos⁡θ=PNPQ=x−x1rsin⁡θ=QNPQ=y−y1r

From the above two equation
x−x1cos⁡θ=y−y1sin⁡θ=r

Also,
x=x1+rcos⁡θy=y1+rsin⁡θ

are parametric equations of straight-line AB

Equation of line parallel to the x-axis

Let the line pass through point A(x1,y1) and be parallel to the axis, i.e., horizontal.
Here, the slope of a line is zero or we can say that m=0so, the equation of the line is y−y1=0 or y=y1
For any point on the line, the value of ordinate is, i.e., each y1 point on the line is at a distance y1∣ from the x-axis.
So the equation of locus is y=y1
Let the line pass through point A(x1,y1) and be parallel to the y -axis, ie., vertical.
Here, the slope of the line is infinity, ie,
So, the equation of the line is x=x1

Equation of line parallel or perpendicular to the given line

Let the given line be ax+by+c=0
The slope of the line is −a/b Then the slope of the line parallel to the given line is −a/b So, the equation of the line parallel to the given line is ax+by+c=0 The value of c can be obtained using some condition given in question.

Now, the slope of the line perpendicular to the given line is b/a So, the equation of the line perpendicular to the given line is bx−ay+c=0

Solved Examples Based on Equation of Straight Line

Example 1: Let the equations of two adjacent sides of a parallelogram ABCD be 2x−3y=−23 and 5x+4y=23. If the equation of its one diagonal AC is 3x+7y=23 and the distance of A from the other diagonal is d , then 50 d2 is equal to [JEE MAINS 2023]

Solution

A \& C point will be (−4,5)&(3,2)
midpoint of AC will be (−12,72)
equation of diagonal BD is
y−72=72−12(x+12)⇒7x+y=0

Distance of A from diagonal BD
=d=2350⇒50d2=(23)250d2=529

Hence, the answer is 529

Example 2: Let ABC be a triangle with A(−3,1) and ∠ACB=θ,0<θ<π2. If the equation of the median through B is 2x+y−3=0 and the equation of angle bisector of C is 7x−4y−1=0, then tan θ is equal to [JEE MAINS 2021]

Solution

Let C be (p,q)
∴E is (p−32,q+12)

It lies on 2x+y−3=0
⇒p−3+q+12−3=0⇒2p+q=11−−−(i)

Also (p.q) lies on 7x−4y−1=0
7p−4q−1=0−−−−−(ii)

From (i) \& (ii) ⇒C(3,5)
∴ Slope of AC=5−13+3=23&
Slope of CF=74
Angle between ACandC F=θ2
⇒tan⁡θ2=|23−741+23,74|⇒tan⁡θ2=12⇒tan⁡θ=2tan⁡θ21−tan2⁡θ2=43

Hence, the answer is 43

Example 3: Let the normal at a point P on the curve y2−3x2+y+10=0 intersect the y -axis at (0,32). If m is the slope of the tangent at P to the curve, then |m|is equal to
[JEE MAINS 2020]

Solution:
2yy′+y′−6x=0y′=6x2y+1
−1y′=−(2y+1)6x (slope of the normal)
Equation of the normal y−y1=−(2y1+1)6x1(x−x1)
Normal intersect at (0,3/2)
32−y1=−(2y1+1)6x1(0−x1)8y1−8=0y1=1x1=±2|m|=4

Hence, the answer is 4.

Example 4: Two sides of a rhombus are along the lines, x−y+1=0 and 7x−y−5=0. If its diagonals intersect at (−1,−2), then which one of the following is a vertex of this rhombus?
[JEE MAINS 2016]

Solution: Slope point form of a straight line -
y−y1=m(x−x1)m→ slope
(x1,y1)→ point through which the line passes

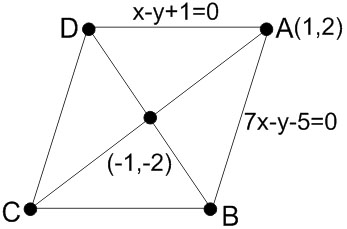
The point of intersection of AB and AD is A(1,2)
Let C be (x1,y1)x1+12=−1 and y1+22=−2x=−3;y=−6C(−3,−6)

Slope of
AC=2+21+1=2

Hence, the slope of
BD=−12
equation of
equation of BD⇒y+2x+1=−122y+4=−x−1BD:x+2y+5=0

Point (13,−83) satisfies the line BD
Hence, the answer is (13,−83)

Example 5: Let PS be the median of the triangle with vertices P(2, 2), Q(6,-1), and R(7, 3). The equation of the line passing through (1,-1) and parallel to PS is : [JEE MAINS 2014]

Solution: |Slope point form of a straight line -
y−y1=m(x−x1)m→ slope
(x1,y1)→ point through which the line passes

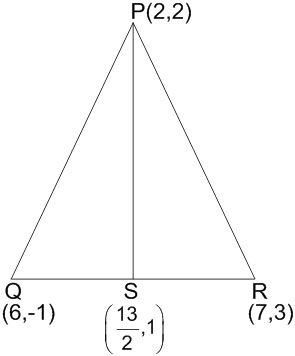
the midpoint of OR is (132,1)
The slope of PS=−192=−29
and line passes through (1,−1)
y+1x−1=−29
2x+9y+7=0
Hence, the answer is 2x+9y+7=0.

Summary

The equation of a straight line provides a relationship between variables and constants. It describes the characteristics of the line like its slope and intercept. Understanding different types of equations of straight lines is necessary as it helps in various geometrical and algebraic problems.The equation of straight lines passing through a given point and making a specified angle with a given line can be determined using principles of coordinate geometry and trigonometry.

Frequently Asked Questions (FAQs)

1. What is a straight line?

It is a curve such that all points on the line segment joining any two points on it lie on it. Every equation of first degree in x, and y represents a straight line. The general equation of a straight line is given as ax + by +c=0 where a,b, and c are real numbers and at least one of a and b is non-zero.

2. What is the equation of a straight line if slope and intercept are given?

3. What is the equation of a straight line whose slope is given as ' $m$ ' and passes through the point $\left(x_1, y_1\right)$ ?

The equation of a straight line whose slope is given as ' m ' and passes through the point (x1,y1) is y−y1=m(x−x1).

4. What is the equation of a straight line that makes intercepts ' $a$ ' and ' $b$ ' on the X -axis and Y -axis respectively?

The equation of a straight line which makes intercepts 'a' and 'b' on the X -axis and Y -axis respectively is given by
xa+yb=1.

5. What is the equation of a line perpendicular to the given line?

Equation of line perpendicular to the given line. Let the given line be ax+by+c=0. The slope of the line is −a/b. Then the slope of the line parallel to the given line is −a/b Activate Windows

6. How can you determine if three points are collinear using their coordinates?

Three points (x1, y1), (x2, y2), and (x3, y3) are collinear if the slope between any two pairs of points is the same. Alternatively, you can use the area of the triangle formed by these points; if it's zero, the points are collinear.

7. How does the point-slope form of a line equation relate to its graph?

The point-slope form, y - y1 = m(x - x1), directly relates to a point (x1, y1) on the line and the slope m. It's useful when you know a point on the line and its slope, allowing you to easily generate other points.

8. What is the significance of the distance formula in relation to line equations?

The distance formula, derived from the Pythagorean theorem, is used to find the distance between two points. It's crucial in deriving the point-slope form and in calculating the distance from a point to a line.

9. How can you use the concept of a line to understand and solve differential equations?

Many first-order differential equations can be visualized as direction fields, where short line segments represent the slope at various points. The solutions to these equations are curves that are tangent to these line segments at each point.

10. How does the slope-intercept form of a line differ from the general form?

The slope-intercept form is y = mx + b, where m is the slope and b is the y-intercept. It's a more specific version of the general form, explicitly showing the slope and y-intercept, making it easier to graph and interpret the line's behavior.

11. What does the slope of a line represent geometrically?

The slope represents the steepness and direction of the line. Geometrically, it's the change in y-coordinate divided by the change in x-coordinate between any two points on the line, often described as "rise over run."

12. What is the significance of the y-intercept in a line equation?

The y-intercept is the point where the line crosses the y-axis. In the equation y = mx + b, b represents the y-intercept. It tells you the starting point of the line on the y-axis when x = 0.

13. How does changing the slope affect a line's appearance on a graph?

Changing the slope affects the line's steepness and direction. A larger positive slope makes the line steeper upward, while a larger negative slope makes it steeper downward. A slope near zero results in a nearly horizontal line.

14. How can you convert between slope-intercept and general forms of a line equation?

To convert from y = mx + b to Ax + By + C = 0, rearrange to -mx + y - b = 0. Then A = -m, B = 1, and C = -b. To convert back, solve the general form for y in terms of x.

15. How does the two-point form of a line equation work?

The two-point form, (y - y1)/(y2 - y1) = (x - x1)/(x2 - x1), uses two known points (x1, y1) and (x2, y2) on the line to determine its equation. It's based on the concept that any point on the line will have the same relative position between these two points.

16. How can you determine if a point lies on a given line?

Substitute the x and y coordinates of the point into the line equation. If the equation is satisfied (becomes a true statement), the point lies on the line. If not, the point is off the line.

17. How does the concept of a line extend to higher dimensions?

In higher dimensions, a line is defined by a point and a direction vector. The parametric form x = x0 + tv, where x and x0 are n-dimensional points, v is a direction vector, and t is a scalar parameter, extends to any number of dimensions.

18. How does the concept of a directional vector relate to a line's equation?

A directional vector is parallel to the line. In the equation y = mx + b, the vector (1, m) is a directional vector. It can be used to generate points on the line and is perpendicular to the normal vector.

19. What is the geometric interpretation of the linear combination of two line equations?

A linear combination of two line equations represents a line that passes through the intersection point of the original lines (if they intersect). This concept is fundamental in solving systems of linear equations and in linear algebra.

20. How can you use matrices to represent and manipulate line equations?

Line equations can be represented as matrix equations. For example, Ax + By + C = 0 can be written as [A B][x y]^T = -C. This allows for the use of matrix operations to solve systems of lines and perform transformations.

21. What is the role of the cross product in determining properties of lines in 3D space?

In 3D, the cross product of two vectors lying on a line gives a vector perpendicular to the line. This is useful for finding normal vectors to planes containing the line and for determining if two lines are parallel or skew.

22. How does the concept of slope relate to the angle a line makes with the x-axis?

The slope m is related to the angle θ that the line makes with the positive x-axis by the equation m = tan(θ). This relationship allows you to convert between slope and angle representations of a line's direction.

23. What does the x-coefficient represent in the general form of a line equation?

In the general form Ax + By + C = 0, the coefficient A represents the negative of the y-component of the normal vector to the line. It plays a role in determining the line's orientation and slope.

24. What is the significance of the normal vector in relation to a line's equation?

The normal vector is perpendicular to the line. In the general form Ax + By + C = 0, the vector (A, B) is normal to the line. This vector is crucial in determining the line's orientation and in calculations involving perpendicular lines.

25. What is the relationship between a line's equation and its perpendicular bisector?

The perpendicular bisector of a line segment is itself a line. Its equation can be found by using the midpoint of the segment and the negative reciprocal of the original line's slope. This concept is crucial in geometry and computational geometry.

26. How does the concept of a line integral relate to line equations?

A line integral calculates a quantity (like work or flux) along a path defined by a line. The line equation provides the path for integration. This concept is fundamental in vector calculus and physics, especially in electromagnetic theory.

27. How can you find the x-intercept of a line given its equation?

To find the x-intercept, set y = 0 in the line equation and solve for x. This gives you the point where the line crosses the x-axis.

28. How does the concept of a line relate to linear functions in algebra?

A linear function f(x) = mx + b is essentially the same as a line equation y = mx + b. The graph of a linear function is a straight line, and the concepts of slope and y-intercept apply directly to the function's behavior.

29. What happens to a line equation when you translate the line parallel to itself?

When a line is translated parallel to itself, its slope remains the same, but the y-intercept changes. In y = mx + b form, only b changes. In general form, only C changes while A and B remain constant.

30. What is the general form of a straight line equation?

The general form of a straight line equation is Ax + By + C = 0, where A, B, and C are constants, and A and B are not both zero. This form represents any straight line in a two-dimensional plane.

31. How can you determine if two lines are parallel using their equations?

Two lines are parallel if they have the same slope. In slope-intercept form (y = mx + b), compare the m values. In general form (Ax + By + C = 0), compare the ratios -A/B. If these are equal for both lines, the lines are parallel.

32. What does a negative slope indicate about a line's orientation?

A negative slope indicates that the line descends from left to right on the coordinate plane. As x increases, y decreases, creating a downward slant.

33. What does it mean when a line has an undefined slope?

An undefined slope occurs when a line is vertical (parallel to the y-axis). In this case, the change in x is zero, making the slope calculation (rise/run) impossible. The equation of such a line is x = a constant.

34. What is the relationship between perpendicular lines and their slopes?

Perpendicular lines have slopes that are negative reciprocals of each other. If one line has a slope m, its perpendicular line will have a slope of -1/m. This means their slopes multiply to give -1.

35. What is the role of lines in understanding and representing linear programming problems?

In linear programming, constraints and objective functions are represented by lines (or hyperplanes in higher dimensions). The feasible region is bounded by these lines, and the optimal solution often lies at the intersection of constraint lines.

36. How can you use the concept of a line to understand and solve systems of linear inequalities?

Lines form the boundaries of regions defined by linear inequalities. Understanding how these lines intersect and the regions they bound is crucial in linear programming and optimization problems in operations research and economics.

37. What is the relationship between lines and linear transformations?

Linear transformations, represented by matrices, can be applied to lines. They preserve collinearity and ratios of distances. Understanding this relationship is crucial in computer graphics, physics, and engineering for modeling and simulations.

38. What is the significance of the reduced row echelon form in solving systems of linear equations?

The reduced row echelon form simplifies a system of linear equations, making it easier to solve. For lines, it can quickly reveal if lines are parallel, intersecting, or coincident by transforming their equations into a standardized form.

39. What is the geometric interpretation of the general form Ax + By + C = 0?

Geometrically, this form represents the line as the set of points (x, y) that satisfy the linear equation. A and B together determine the line's direction (normal vector), while C affects its position relative to the origin.

40. What is the significance of Hesse normal form of a line equation?

The Hesse normal form, x cos(θ) + y sin(θ) = p, represents a line using its normal vector angle θ and its perpendicular distance p from the origin. This form is useful in computational geometry and image processing for efficient line representations.

41. How can you use the concept of duality to relate points and lines?

In projective geometry, there's a duality between points and lines. A point (a, b) corresponds to the line ax + by + 1 = 0, and vice versa. This duality principle simplifies many geometric proofs and constructions.

42. How does the concept of a line relate to the theory of linear codes in information theory?

In coding theory, linear codes can be thought of as subspaces of vector spaces over finite fields. The properties of lines (like linearity and dimension) extend to these codes, influencing their error-correcting capabilities and efficiency.

43. What is the parametric form of a line equation, and how is it useful?

The parametric form expresses x and y coordinates separately in terms of a parameter t: x = x0 + at, y = y0 + bt. It's useful for describing motion along a line, finding intersections, and in computer graphics for rendering lines.

44. How can you use the concept of vector projection to find the point on a line closest to a given point?

Vector projection allows you to project a vector from the given point onto the line's direction vector. This projection, when added to a point on the line, gives the closest point. It's useful in minimizing distances and in computer graphics.

45. What is the role of homogeneous coordinates in representing lines?

Homogeneous coordinates allow lines to be represented as points in projective geometry. The general form Ax + By + C = 0 becomes a point (A:B:C) in projective space. This is useful in computer vision and graphics for handling parallel lines and points at infinity.

46. How does the concept of a line generalize to curves and non-linear functions?

A line is the simplest form of a curve, with constant slope everywhere. Non-linear functions can be approximated by lines (tangent lines) at specific points, forming the basis of calculus and differential geometry.

47. How can you use complex numbers to represent lines in the complex plane?

In the complex plane, a line can be represented by the equation az + bz̄ + c = 0, where z is a complex variable, z̄ is its conjugate, and a, b, c are complex constants. This representation allows for elegant solutions to certain geometric problems.

48. How does the concept of a line generalize to manifolds in differential geometry?

In differential geometry, a line generalizes to a geodesic, which is the shortest path between two points on a curved surface or manifold. Understanding this generalization is crucial in general relativity and in optimizing paths on complex surfaces.

49. What is the relationship between lines and hyperplanes in higher-dimensional spaces?

In higher dimensions, a line generalizes to a hyperplane. While a line divides a 2D plane into two parts, a hyperplane divides an n-dimensional space into two parts. This concept is fundamental in machine learning, particularly in support vector machines and decision boundaries.

50. How does the concept of a line extend to non-Euclidean geometries?

In non-Euclidean geometries like spherical or hyperbolic geometry, the concept of a "line" (geodesic) can be curved. For example, on a sphere, great circles play the role of lines. Understanding these generalizations is crucial in modern physics and cosmology.

51. What is the significance of projective transformations on lines?

Projective transformations preserve lines but may change their apparent orientation and intersection points. This is crucial in computer vision and graphics for understanding how 3D scenes project onto 2D images and in creating perspective drawings.

52. How can you use the discriminant to determine the nature of intersection between a line and a circle?

The discriminant in the quadratic equation resulting from solving a line-circle system determines the intersection. A positive discriminant means two intersections, zero means tangency (one intersection), and negative means no intersection.

53. What is the significance of the line at infinity in projective geometry?

The line at infinity is a concept in projective geometry where parallel lines are considered to intersect. It's represented by the equation z = 0 in homogeneous coordinates (x:y:z). This concept unifies the treatment of intersecting and parallel lines.

54. What is the role of eigenvectors in relation to lines in linear transformations?

Eigenvectors of a linear transformation represent directions that are only scaled, not rotated, by the transformation. Lines in these directions maintain their orientation, which is crucial in understanding the behavior of linear systems and in principal component analysis.

55. What is the significance of Plücker coordinates in representing lines in 3D space?

Plücker coordinates represent a line in 3D using six coordinates, based on a point on the line and a direction vector. This representation is useful in robotics and computer vision for efficient line intersection and closest point calculations.