Pair of Straight Lines: Formulas & Solved Examples

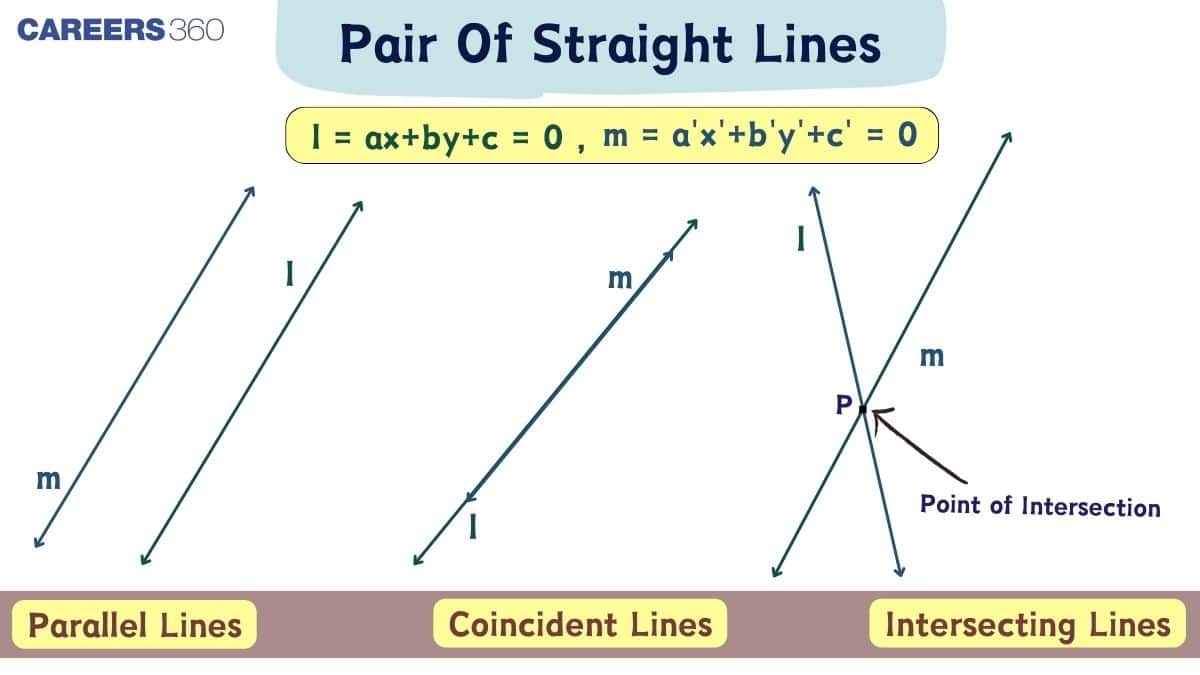
What is a Pair of Straight Lines?

A pair of straight lines can be represented as a product of two linear equations in $x$ and $y$, representing a straight line.

If the equation of two straight lines is $a_1 x+b_1 y+c_1=0$ and $a_2 x+b_2 y+c_2=$ 0, then the combined or joint equation of these two lines is
$a x^2+2 h x y+b y^2+2 g x+2 f y+c=0$

Derivation of the Equation of a Pair of Straight Lines

$\left(a_1 x+b_1 y+c_1\right)\left(a_2 x+b_2 y+c_2\right)=0$

Multiplying the brackets, we get
$a_1 a_2 x^2 + (a_1 b_2 + a_2 b_1) x y + b_1 b_2 y^2 + (a_1 c_2 + c_1 a_2) x + (b_1 c_2 + c_1 b_2) y + c_1 c_2 = 0$

Here, the coefficients can be renamed, and this equation can be rewritten as
$a x^2+2 h x y+b y^2+2 g x+2 f y+c=0$

So, a pair of straight lines is represented by a two-degree equation in $x$ and $y$.

Condition for a general two-degree equation to represent a pair of straight lines

A general two degree equation $a x^2+2 h x y+b y^2+2 g x+2 f y+c=0$ may represent $a$

• Pair of straight lines, or

• Circle, or

• Parabola, or

• Ellipse, or

• Hyperbola

To identify which of the following curves is represented by a given equation of a straight line, we have a determinant

$\Delta = \begin{vmatrix} a & h & g \\ h & b & f \\ g & f & c \end{vmatrix}$

If this determinant equals zero, then the given equation represents a pair of straight lines.

Types of Pair of Straight Lines

A pair of straight lines represented by a second-degree equation can exhibit different relationships based on the nature of their interaction. Understanding these types: intersecting lines, coincident lines, and parallel or imaginary lines, is crucial when solving geometry-based questions.

Intersecting Lines

A pair of intersecting straight lines means the two lines cross each other at a single point. For this to happen, the equation must satisfy:

• $\Delta = 0$ (condition for a pair of lines), and

• $ h^2-ab> 0$ (condition for real and distinct lines)

These lines usually intersect at the origin when the equation is homogeneous. Graphically, they form an “X” shape, and the angle between the pair of lines can be calculated using a specific trigonometric formula. Recognising this type helps students solve questions on the angle between lines and equation factorisation.

Coincident Lines

When both lines in the pair lie exactly over one another, they are called coincident lines. In this case, the pair represents the same line repeated twice, and the conditions are:

• $\Delta = 0$

• $h^2 - ab = 0$

Parallel or Imaginary Lines

In some cases, the quadratic equation may represent parallel straight lines or even imaginary lines (non-real). These occur when:

• $\Delta = 0$

• $h^2 - ab < 0$

If the lines are real and parallel, they have the same slope but different intercepts. These are usually represented by non-homogeneous second-degree equations, where the constant term $c$ is not zero. However, if the lines are imaginary, they do not intersect on the real plane, which means they are complex conjugates with no real points of intersection.

Condition for a Second-Degree Equation to Represent a Pair of Straight Lines

A general second-degree equation in two variables is given by:

$ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0$

This equation may represent a pair of straight lines, a circle, a parabola, or other conic sections, depending on certain conditions. To specifically determine whether the equation represents a pair of straight lines, we use key criteria involving the discriminant and coefficients. Students often search for how to identify a pair of straight lines from a second-degree equation, and the key lies in satisfying the right condition.

Discriminant Condition Explained

The most crucial part of identifying a pair of straight lines is checking the discriminant condition. The condition is:

$\Delta = abc + 2fgh - af^2 - bg^2 - ch^2 = 0$

If this discriminant $\Delta$ equals zero, the second-degree equation represents a pair of straight lines. This is a powerful test when verifying whether a conic breaks down into two straight lines or not.

Derivation of a general two-degree equation to represent a pair of straight lines

If we write the equation as a quadratic in x , where $\mathrm{a} \neq 0$
$a x^2+2 x(h y+g)+\left(b y^2+2 f y+c\right)=0$

Solving for ' $x$ ', we get
$x = \frac{-2(hy + g) \pm \sqrt{4(hy + g)^2 - 4a(by^2 + 2fy + c)}}{2a}$

$x = \frac{-(hy + g) \pm \sqrt{(h^2 - ab)y^2 + 2(gh - af)y + (g^2 - ac)}}{a}$

For this equation to represent two straight lines, we must have ' $x$ ' as a linear expression in ' $y$ '. For that, the value under the square root must be a perfect square of some linear expression in ' $y$ '. For this to happen, the Discriminant of the quadratic equation in $y$ (the equation inside the root) must be zero.

So, Discriminant of $\left(h^2-a b\right) y^2+2(g h-a f) y+\left(g^2-a c\right)$ is 0
$4(gh - af)^2 - 4(h^2 - ab)(g^2 - ac) = 0$

$\Rightarrow abc + 2fgh - af^2 - bg^2 - ch^2 = 0$

This is the condition for which $a x^2+2 h x y+b y^2+2 g x+2 f y+c=0$ represents a pair of straight lines.

This condition can also be written in a determinant form as
$\begin{vmatrix} a & h & g \\ h & b & f \\ g & f & c \end{vmatrix} = 0$

Condition for Real and Distinct Straight Lines

Once it is confirmed that the equation represents a pair of lines (i.e., $\Delta = 0$), the next step is to check whether the lines are real and distinct.

This depends on the expression:

$h^2 - ab > 0$

If $h^2-ab$ is greater than 0, the pair of lines is real and intersecting at a point (usually the origin in the homogeneous case). This is one of the most commonly used conditions for a real and distinct pair of straight lines in coordinate geometry problems.

Condition for Coincident and Parallel Lines

For coincident lines, the pair of straight lines must lie on top of each other. In such a case:

• $\Delta = 0$ (same as before), and

• $h^2 - ab = 0$

This implies that both lines are not just real but also identical in every way. This case is often tested in questions asking for the difference between intersecting and coincident straight lines.

For parallel lines, the equation must not be homogeneous, and the lines will never meet. They can occur under special arrangements of coefficients where the lines share the same slope but have different intercepts.

Point of Intersection of a Pair of Straight Lines

To get the point of intersection, first find the separate equations of the straight lines and solve them simultaneously.
Or
The point of intersection of a pair of straight lines can also be determined with the help of partial differentiation
The point of Intersection of a Pair of Straight Lines is
$\therefore \quad(x, y)=\left(\frac{b g-f h}{h^2-a b}, \frac{a f-g h}{h^2-a b}\right)$

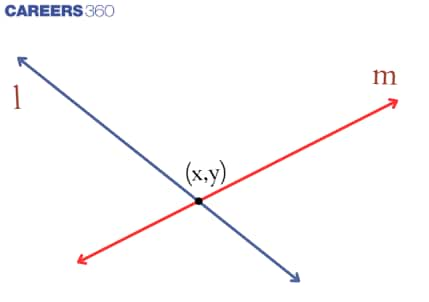
Derivation of the Point of Intersection of a Pair of Straight Lines

Let $\phi \equiv \mathrm{ax}^2+2 \mathrm{hxy}+\mathrm{by}^2+2 \mathrm{gx}+2 \mathrm{fy}+\mathrm{c}=0$

Differentiating $\phi$ with respect to $x$, keeping $y$ constant, we get:

$\frac{\partial \phi}{\partial x} = 2ax + 2hy + 2g$

Similarly, differentiating $\phi$ with respect to $y$, keeping $x$ constant, we get:

$\frac{\partial \phi}{\partial y} = 2hx + 2by + 2f$

For the point of intersection, we set:

$\frac{\partial \phi}{\partial x} = 0$ and $\frac{\partial \phi}{\partial y} = 0$

Thus, we have: $ax + hy + g = 0$ and $hx + by + f = 0$

Solving the two equations using cross-multiplication, we get:

$\frac{x}{fh - bg} = \frac{y}{gh - af} = \frac{1}{ab - h^2}$

Therefore: $(x, y) = \left( \frac{bg - fh}{h^2 - ab}, \frac{af - gh}{h^2 - ab} \right)$

Note: In the above equations, $2 a x+2 h y+2 g=0$ and $2 h x+2 b y+2 f=0$ are NOT the equations of components of the straight line.

Applications in Algebra and Geometry

The concept of a pair of straight lines has widespread applications in both algebra and geometry, particularly in simplifying quadratic expressions, solving spatial problems, and analysing conic sections. Whether you're dealing with second-degree polynomials, constructing geometric diagrams, or interpreting equations in the coordinate plane, mastering the behaviour and properties of line pairs is essential.

Factorisation of Second-Degree Polynomials

One of the most important algebraic uses of a pair of straight lines is in the factorisation of second-degree polynomials. When a second-degree equation satisfies the condition for representing a pair of lines ($\Delta = 0$), it can be broken into two linear factors:

$ax^2 + 2hxy + by^2 + 2gx + 2fy + c = (L_1)(L_2)$

Where $L_1$ and $L_2$ are the equations of the two straight lines. This technique is useful in simplifying expressions and solving quadratic equations, especially when identifying real and distinct roots or geometric configurations in coordinate problems.

Use in Solving Geometrical Problems

In geometry, pairs of straight lines help solve problems related to intersection points, angles between lines, perpendicularity, and distance between parallel lines. They often appear in problems involving:

• Finding the angle between two intersecting lines

• To check if the line is equally inclined with two intersecting lines

• Locating the point of intersection

• Verifying whether lines are coincident or parallel

This makes the concept extremely relevant in Class 11 coordinate geometry and in real-life modeling of intersecting paths or edges in design and architecture.

Role in Coordinate Geometry and Conic Sections

In coordinate geometry, a pair of straight lines acts as a special case of a conic section, specifically, a degenerate conic. When a general second-degree equation reduces to a product of two linear factors, the conic (like a circle, ellipse, or hyperbola) collapses into a pair of lines.

Solved Examples Based on a Pair of Straight Lines

Example 1: The absolute value of the difference of the slopes of the lines $x^2\left(\sec ^2 \theta-\sin ^2 \theta\right)-2 x y \tan \theta+y^2 \sin ^2 \theta=0$ is :

1) -2

2) 43832

3) 2

4) 1
Solution:

The angle between a pair of lines -

$\tan \theta=2\left|\frac{\sqrt{h^2-a b}}{a+b}\right|$ wherein

$\text { Equation : } a x^2+b y^2+2 h x y+2 g x+2 f y+c=0$

$\quad x^2\left(\sec ^2 \theta-\sin ^2 \theta\right)-2 x y \tan \theta+y^2 \sin ^2 \theta=0$

$\left|m_1-m_2\right|=\sqrt{\left(m_1+m_2\right)^2-4 m_1 m_2}$

$\sqrt{\left(\frac{2 \tan \theta}{\sin ^2 \theta}\right)^2-4\left(\frac{\sec ^2 \theta-\sin ^2 \theta}{\sin ^2 \theta}\right)}=2$

Hence, the answer is option 3.

Example 2: The equation $x^2 y^2-2 x y^2-3 y^2-4 x^2 y+8 x y+12 y=0$ represents

1) a pair of straight lines

2) a pair of straight lines and a circle

3) a pair of straight lines and a parabola

4) a set of four lines forming a square

Solution:

Condition for a pair of straight lines -

$\Delta=0$ wherein

$\triangleright=a b c+2 f g h-a f^2-b g^2-c h^2$

For conic:

$a x^2+b y^2+2 h x y+2 g x+2 f y+c=0$

$x^2 y^2-2 x y^2-3 y^2-4 x^2 y+8 x y+12 y=y^2\left(x^2-2 x-3\right)-4 y\left(x^2-2 x-3\right)=0$

$\Rightarrow y(y-4)(x-3)(x+1)=0 \quad \Rightarrow y=0, y=4, x=3, x=-1$

So, the equation represents four straight lines which evidently form a square.

Hence, the answer is option 4.

Example 3: If the sum of the slopes of the lines given by $x^2-2 c x y-7 y^2=0$ is four times their product, then $c$ has the value

1) 2

2) -1

3) 1

4) -2
Solution:

$x^2=2 c x y-7 y^2=0$

Divide equation by

$x^2 ; \frac{y}{x}=m$

$1-2 c m-7 m^2=0$

$7 m^2+2 c m-1=0$

$m_1+m_2=4 m_1 m_2$

$-\frac{2 c}{7}=4 \times \frac{-1}{7} \quad C=2$

Hence, the answer is option 1.

Example 4: If the pairs of straight lines $x^2-2 p x y-y^2=0$ and $x^2-2 q x y-y^2=0$ be such that each pair bisects the angle between the other pair, then

1) $p=-q$

2) $p q=1$

3) $p q=-1$

4) $p=q$

Solution:

$x^2+2 p x y-y^2=0$

and $x^2-2 p x y-y^2=0$

They bisect the angle between the other pair

The equation of bisector is given by

$\frac{x^2-y^2}{1-(-1)}=\frac{x y}{-p} \Rightarrow x^2+\frac{2}{p} x y-y^2=0$

$\text { So } \frac{2}{p}=-2 q \Rightarrow p q=-1$

Hence, the answer is option 3.

Example 5: The pair of lines represented by $3 a x^2+5 x y+\left(a^2-2\right) y^2=0$ and perpendicular to each other for

1) two values of a

2) $\forall a \in R$

3) for one value of a

4) for no values of a

Solution:

$3 a x^2+5 x y+\left(a^2-2\right) y^2=0$

For perpendicular lines, the sum of the coefficients of $x^2$ and $y^2=0$

$a^2-2+3 a=0$

$a^2+3 a-2=0$

So, there are two real values of a.

Hence, the answer is option 1.

List of Topics related to Pair of Straight Lines

Understanding the pair of straight lines becomes easier when you're familiar with related topics in coordinate geometry. This list includes key concepts such as the equation of a straight line, angle between two lines, parallel and perpendicular lines, and the point of intersection formula, all of which support a deeper grasp of line-based problems and derivations.

NCERT Resources

Explore essential NCERT resources for mastering the topic of straight lines in Class 11. Access detailed NCERT solutions, concise notes, and well-explained exemplar problems from Chapter 10: Straight Lines to build strong conceptual clarity and improve exam performance.

NCERT Solutions for Class 11 Chapter 10 - Straight Lines

NCERT Notes for Class 11 Chapter 10 - Straight Lines

NCERT Exemplar Solutions for Class 11 Chapter 10 - Straight Lines

Practice Questions based on a Pair of Straight Lines

Strengthen your understanding of the pair of straight lines through targeted MCQs and practice questions. This section covers a variety of concepts, including the point of intersection formula, angle between lines, bisectors, and equally inclined lines, ideal for Class 11 revision and competitive exam preparation.

Pair Of Straight Lines - Practice Question MCQ