Subsets and types of subsets

A subset is a fundamental concept in set theory, forming the basis for various operations and relationships in mathematics. When we say one set is a subset of another, it means that every element of the first set is also an element of the second. Subsets are essential in understanding how sets relate to each other and are widely used in algebra, logic, and real-life problem-solving.

This Story also Contains

1. What is a Subset in Maths?
2. Types of Subsets
3. Properties of Subsets
4. Power Set of a Set
5. Intervals as Subsets of Real Numbers
6. Subset Examples
7. Practice Questions based on Subsets

In this article on Subsets, Proper Subset, Improper Subset, Intervals, we will define subsets and types of subsets, also explain what is a subset in Maths, explore the types of subsets, and discuss the properties of subsets with clear subsets examples. You’ll also learn about the classifications of subset, including proper and improper subsets, and understand how intervals fit into the broader context of set theory.

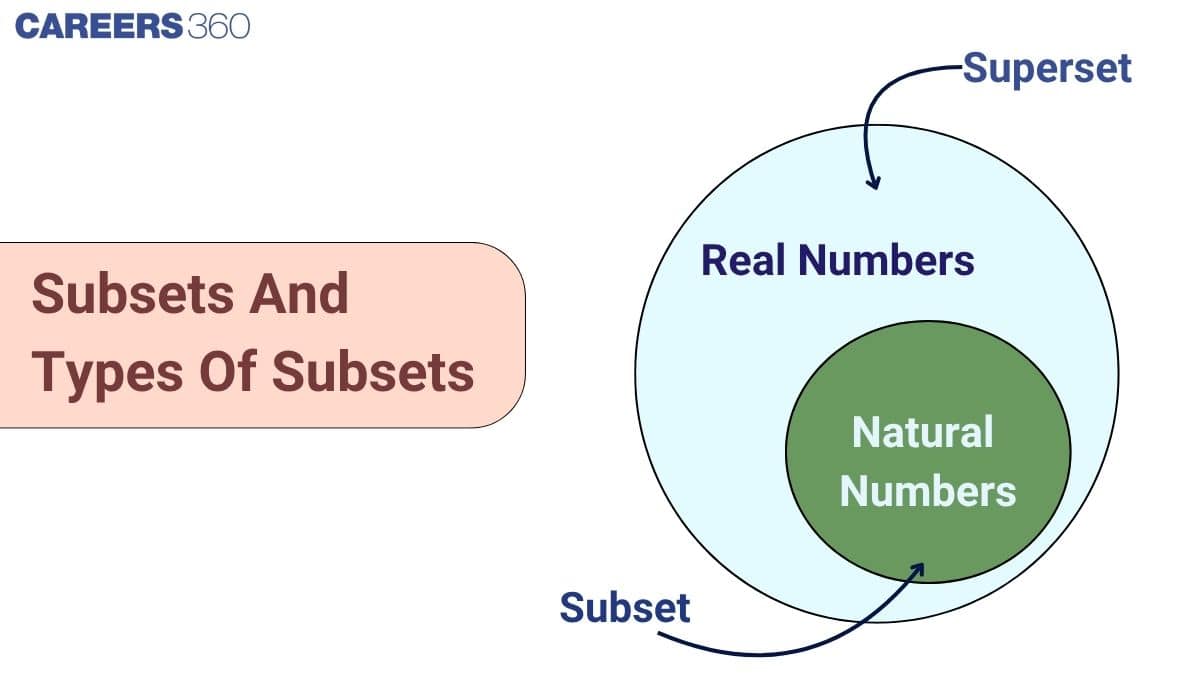
What is a Subset in Maths?

A subset is a fundamental idea in set theory and mathematics as a whole. It helps us understand how collections of elements relate to each other, especially in topics like algebra, geometry, and statistics. A set is simply a well-defined collection of distinct objects, known as elements, which may include numbers, letters, people, or other items. Sets are typically represented by capital letters such as $A, B, C, S, U, V$. The idea of a subset emerges when we compare two sets and check whether all elements of one set are also present in another.

In this context, a subset refers to a set whose elements are entirely contained within another set. Understanding this relationship is essential for working with data groups, mathematical functions, and logical reasoning.

Examples of Subsets

In mathematical terms, if $A$ and $B$ are two sets, then $A$ is a subset of $B$, written as $A \subseteq B$, if every element of $A$ is also an element of $B$. This relationship is formally defined as:

$A \subseteq B \Leftrightarrow \forall x(x \in A \Rightarrow x \in B)$

Let’s take a few simple examples to understand this:

Example 1:
Let $A = \{1, 2, 3\}$ and $B = \{1, 2, 3, 4, 5\}$
Since every element of $A$ is present in $B$, we can say:
$A \subseteq B$

Example 2:
Let $P = \{a, b\}$ and $Q = \{a, b, c\}$
Then:
$P \subseteq Q$

Example 3:
Let $X = \{7, 8\}$ and $Y = \{6, 7, 8, 9\}$
Then clearly:
$X \subseteq Y$

Symbol and Notation of Subsets in Set Theory

In set theory, the notation for subsets plays a crucial role in expressing mathematical relationships. The standard symbols include:

• $A \subseteq B$: $A$ is a subset of $B$ (possibly equal).

• $A \subset B$: $A$ is a proper subset of $B$ (all elements of $A$ are in $B$, but $A \ne B$).

• $A \not\subseteq B$: $A$ is not a subset of $B$.

These notations help represent inclusion relationships between sets in a clear and concise way.

What is the difference between $\subseteq$ and $\subset$ ? The symbol $\subseteq$ represents subset while $\subset$ represents proper subset.

For example:

If $M = \{2, 4\}$ and $N = \{2, 4, 6\}$, then:
$M \subset N$

However, if $M = \{2, 4, 6\}$ and $N = \{2, 4, 6\}$, then:
$M \subseteq N$ but not $M \subset N$

Real-Life Examples

Subsets are not just abstract concepts; they are used frequently in real-world contexts. Consider the following examples:

Example 1: Subjects in a Class
If Set $A = \{\text{Math, Science}\}$ and Set $B = \{\text{Math, Science, History, English}\}$, then:
$A \subseteq B$
Here, the subjects Math and Science are part of a larger curriculum.

Example 2: Team Members
If $A = \{\text{Riya, Karan}\}$ and $B = \{\text{Riya, Karan, Mitali, Aarav}\}$, then:
$A \subseteq B$
This shows a smaller group of team members inside a larger team.

Example 3: Fruits in a Basket
Let $A = \{\text{Apple, Banana}\}$ and $B = \{\text{Apple, Banana, Mango, Orange}\}$. Then:
$A \subseteq B$
This represents a subset of fruits taken from a bigger fruit basket.

These examples show how subsets help in organizing and analyzing grouped data or categories in daily life, education, and business logic.

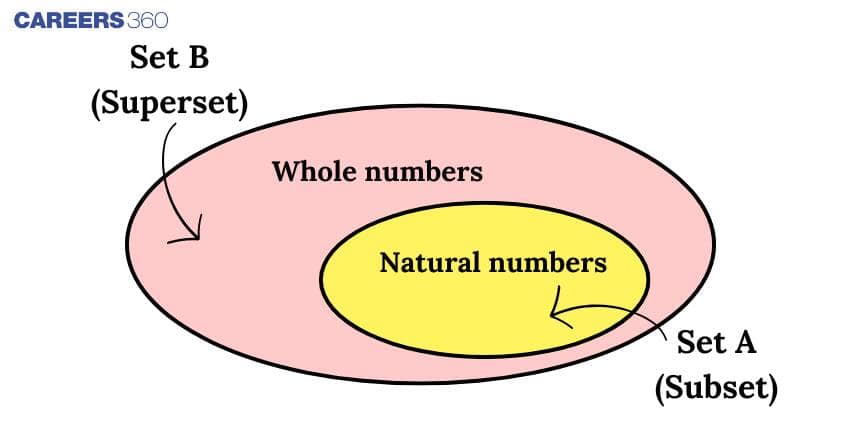
Types of Subsets

In set theory, subsets can be further classified based on how they relate to the original or larger set. Understanding the types of subsets in mathematics helps in analyzing the structure and relationships between sets in more depth. The primary classifications include proper subsets, improper subsets, and special subsets like the empty set and the universal set. Subsets can also be categorized based on whether they are finite or infinite in nature.

Proper Subsets – Definition and Examples

A proper subset is a subset that contains some but not all elements of the original set. In simple terms, if set $A$ is a proper subset of set $B$, it means every element of $A$ is in $B$, but $A$ is not equal to $B$. The notation used is:

$A \subset B$

This symbol $\subset$ is read as “A is a proper subset of B.”

Example:

Let $A = \{1, 2\}$ and $B = \{1, 2, 3\}$, then: $A \subset B$

Total Number of Proper Subsets:

If a set contains $n$ elements, then:

• Total subsets = $2^n$

• Proper subsets = $2^n - 1$

Example:

Let $X = \{1, 2\}$

• Number of elements = $n = 2$

• Total subsets = $2^2 = 4$

• Proper subsets = $2^2 - 1 = 3$

Proper subsets of $X$ are:

$\{\},\{1\},\{2\}\{\}, \{1\}, \{2\}\{\},\{1\},\{2\}$

The only subset not considered proper is $X$ itself, i.e., $\{1, 2\}$.

Improper Subsets – What Makes a Subset Improper?

An improper subset is a subset that is identical to the original set. In fact, every set is always an improper subset of itself. This type of subset does not exclude any element from the parent set. It is an essential concept because it guarantees that every set will always have at least one subset—itself.

Examples:

1. Let $A = \{a, s, c\}$
   Subsets of $A$:
   $\{\}, \{a\}, \{s\}, \{c\}, \{a,s\}, \{a,c\}, \{s,c\}, \{a,s,c\}$
   Here, $\{a,s,c\}$ is the improper subset, all others are proper.

2. Let $B = \{2, 3, 4\}$
   Subsets of $B$:
   $\{\}, \{2\}, \{3\}, \{4\}, \{2,3\}, \{2,4\}, \{3,4\}, \{2,3,4\}$
   $\{2,3,4\}$ is the improper subset of $B$.

Universal Set and Empty Set as Special Subsets

Some subsets have special significance in set theory:

Empty Set ($\emptyset$ or ${}$):

• A set that contains no elements.

• It is a subset of every set.

• It is always considered a proper subset of any non-empty set.

Example:

Let $A = \{x, y\}$, then:

$\emptyset \subset A$

Universal Set ($U$):

• A set that contains all elements under consideration for a particular discussion or problem.

• Every set in the given context is a subset of the universal set.

Example:

If $U = \{1, 2, 3, 4, 5\}$ and $A = \{2, 3\}$, then:

$A \subseteq U$

Finite and Infinite Subsets

Subsets can also be classified based on the number of elements they contain:

Finite Subsets:

• Contain a countable number of elements.

• Can be listed exhaustively.

Example:

$A = \{2, 4, 6\}$ is a finite subset of $B = \{2, 4, 6, 8, 10\}$

$A \subset B$

Infinite Subsets:

• Contain an uncountable or infinite number of elements.

• Often seen in sets of natural numbers, real numbers, etc.

Example:

Let $A = \{2, 4, 6, 8, 10, \dots\}$ be the set of all even natural numbers
and $B = \mathbb{N}$ (set of all natural numbers), then: $A \subset B$

Here, $A$ is an infinite proper subset of the infinite set $B$.

Properties of Subsets

Understanding the properties of subsets is crucial for working efficiently with set operations and relations in mathematics. These properties form the basis for how sets interact and are often used in proving statements or solving problems in algebra, logic, and number theory.

Basic Rules and Characteristics of Subsets

Below are the fundamental rules and characteristics that apply to all subsets:

• Reflexive Property: Every set is always a subset of itself.
  For any set $A$, $A \subseteq A$

• Empty Set Property: The empty set is a subset of every set.
  For any set $A$, $\emptyset \subseteq A$

• Total Number of Subsets: If a set has $n$ elements, then the total number of possible subsets is given by: $2^n$

• Proper Subsets Count: The number of proper subsets of a set with $n$ elements is: $2^n - 1$

• Singleton Set: A set with a single element is called a singleton set and is a subset of any set that contains that element.

Relationship Between Sets and Subsets

The relationship between sets and subsets is hierarchical and directional. It is based on element inclusion:

• If $A \subseteq B$, every element of $A$ is in $B$, but $B$ may contain additional elements.

• If $A \subset B$, then $A$ is a proper subset of $B$, meaning $A$ is not equal to $B$.

• If $A = B$, both sets contain exactly the same elements; hence, $A$ is an improper subset of $B$.

Example:

Let $A = \{1, 2\}$ and $B = \{1, 2, 3\}$, then:

• $A \subset B$ (proper subset)

• $A \subseteq B$ (subset)

• $A \ne B$

Also, note:

• $\emptyset \subseteq A$

• $A \subseteq A$

Important Theorems on Subsets

Several important theorems govern how subsets behave and relate to one another:

Theorem 1:

If $A \subseteq B$ and $B \subseteq C$, then $A \subseteq C$.
(This is known as the transitive property of subsets.)

Theorem 2:

The empty set is a subset of every set:
$\emptyset \subseteq A$

Theorem 3:

If $A$ has $n$ elements, then its power set—the set of all subsets—is denoted by $P(A)$ and contains:
$|P(A)| = 2^n$
where $|\cdot|$ denotes cardinality (number of elements).

Example:

Let $A = \{x, y\}$, then:

• Subsets: $\emptyset$, $\{x\}$, $\{y\}$, $\{x, y\}$

• Total subsets: $2^2 = 4$

Power Set of a Set

The power set of a set is defined as a set of all the subsets (along with the empty set and the original set). The power set of a set Y is denoted by P(Y). If Y has 'n' elements then P(Y) has 2n elements. For example,

• If E = {x, p}, then P(E) = { { }, {x}, {p}, {x, p} }
  Total number of elements = 4 .

• If A = {a, b, c}, then P(A) = { { }, {a}, {b}, {c}, {a, b}, {b, c}, {c, a}, {a, b, c} }
  Observe that A has 3 elements and P(A) has 23 = 8 elements.

Power set of $A$:
$P(A) = \{\emptyset, \{x\}, \{y\}, \{x, y\}\}$

These properties and theorems help in building a strong foundation in understanding types of subsets, set operations, and logical proofs in higher mathematics.

Intervals as Subsets of Real Numbers

In set theory and real analysis, intervals are special types of subsets of real numbers. They represent all real numbers lying between two endpoints and are widely used in functions, calculus, and inequalities. These intervals can be bounded or unbounded and are always subsets of the real number line $ \mathbb{R} $.

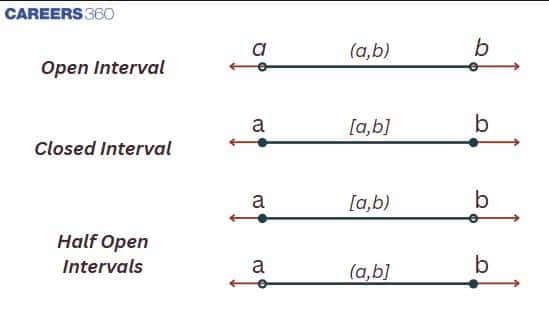
Open, Closed, and Half-Open Intervals

Intervals are classified based on whether their endpoints are included or not:

• Open Interval $(a, b)$:
  Includes all real numbers strictly between $a$ and $b$ (excluding endpoints).
  $(a, b) = \{x \in \mathbb{R} \mid a < x < b\}$

• Closed Interval $[a, b]$:
  Includes all real numbers between $a$ and $b$, including both endpoints.
  $[a, b] = \{x \in \mathbb{R} \mid a \leq x \leq b\}$

• Half-Open Interval $[a, b)$:
  Includes $a$ but not $b$.
  $[a, b) = \{x \in \mathbb{R} \mid a \leq x < b\}$

• $(a, b]$:
  Includes $b$ but not $a$.
  $(a, b] = \{x \in \mathbb{R} \mid a < x \leq b\}$

Graphical Representation of Intervals

On a number line:

• Closed dots represent inclusion of endpoints (used for $[a, b]$).

• Open dots represent exclusion of endpoints (used for $(a, b)$).

Examples:

• $[2, 5]$ → solid dots at 2 and 5

• $(2, 5)$ → open dots at 2 and 5

• $[2, 5)$ → solid dot at 2, open dot at 5

Difference Between Intervals and General Subsets

While intervals are continuous subsets of $\mathbb{R}$, general subsets can be discrete or non-continuous.

• Interval Example:
  $(1, 5) = \{x \in \mathbb{R} \mid 1 < x < 5\}$

• General Subset Example:
  $A = \{1, 2, 3, 5\}$
  (Not an interval, as 4 is missing.)

• Notation: Intervals use (, ), [, ]; subsets use curly braces ${}$.

Infinite Intervals

Intervals may extend infinitely:

• Left-Unbounded:
  $(-\infty, b) = \{x \in \mathbb{R} \mid x < b\}$

• Right-Unbounded:
  $(a, \infty) = \{x \in \mathbb{R} \mid x > a\}$

• Entire Real Line:
  $(-\infty, \infty) = \mathbb{R}$

Subset Examples

Example 1: Let $A$ and $B$ be two sets containing four and two elements respectively. Then the number of subsets of the set $A X B$, each having at least three elements is:

Solution: $A$ set $A$ is said to be a subset of a set $B$ if every element of $A$ is also an element of $B$.
wherein
It is represented by $\subset$. eg. $A \subset B$ if $A=\{2,4\}$ and $B=\{1,2,3,4,5\}$
Let $A$ having elements $\{\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}\}$ and $B$ having $\{\mathrm{e}, \mathrm{f}\}$
Then $A \times B$ having 8 elements and no. of subsets $=2^8=256$
No. of subsets $=\phi,(a e), \ldots \ldots(d f)$ and (ae, be) $\ldots \ldots \ldots=256$

Now $8$ subsets have only one element

$\{ae\},\{af\},\{be\},.......\{df\}$

Similarly

No of the sets having two elements

$\{ae,af\}, \{ae,be\}, .....\{ae,df\}=7$ elements

$\{af,be\},\{af,bf\}..........= 6$ elements

$7 + 6 + 5 + 4 + 3 + 2 + 1 = 28$ (having two elements)

and a subset having a single element $\phi$

$28 + 8+1 = 37$

At least three elements $= 256 - 37 = 219 $

Hence, the answer is $219.$

Example 2: If $A=\{1,2,3,5,7\}$ and $B=\{3,5\}$, then
1) $A \subset B$
2) $B \not \subset A$
3) $A=B$
4) $B \subset A$

Solution: All elements of $B$ are present in $A$ , thus $B \subset A$.
Hence, the answer is the option 4.

Example 3: If a set $A$ has $8$ elements, then the number of proper subsets of the $\operatorname{set} A$ is
Solution: Number of proper subsets $=2^8-1=256-1=255$
Hence, the answer is $255$.

Example 4: If a set has $256$ subsets. How many elements does it have?
1) $5$
2) $7$
3) $8$
4) $9$

Solution: $2^n=256$
$\Rightarrow n=8$

Hence, the answer is the option 3.

Example 5: If a set has $32$ subsets. How many elements does it have?
Solution: As we know, if a set has $n$ elements, it will have $2^n$ subsets.
Thus $2^n=32$

$\Rightarrow n=5$

Hence, the answer is $5$.

Practice Questions based on Subsets

This section offers a set of carefully designed practice questions based on subsets and types of subsets, aimed to boost understanding of key set theory concepts. It includes multiple-choice questions covering finite and infinite sets, singleton sets, power sets, as well as operations like union, intersection, and difference of sets.

Subsets, Proper Subset, Improper Subset, Intervals - Practice Question MCQ

Practice questions on the next topics covering various concepts based on sets, properties of sets such as union, intersection, difference, etc.

Recommended Video based on Subsets

Below is a recommended video that provides a clear and concise explanation of important concepts related to subsets. It covers topics such as subsets and types of subsets: proper and improper subsets, and intervals, helping you build a strong foundation through easy examples.

Watch Now

NCERT Useful Resources

This section provides a collection of valuable NCERT study materials for Class 11 Mathematics Chapter 1 – Sets. It includes comprehensive notes, solved NCERT textbook questions, and exemplar problems based on subsets and types of subsets along with other topics to help you strengthen your understanding and master the concepts effectively.

NCERT Maths Class 11 Chapter 1 Sets Notes

NCERT Maths Class 11 Chapter 1 Sets Solutions

NCERT Maths Exemplar Problems Class 11 Chapter 1 Sets