Union of Sets: Definition, Equation, Formula, Examples, Calculator

Q: What does $\cap$ and $\cup$ mean in math?

$\cap$ represents the intersection of two sets while $\cup$ represents the union of two sets.

Q: What are the factors which determine the complement of a set?

The complement of a set simply means all elements having any relations to the universal set without contacting the elements of the given set.

Q: What does $A \cup B$ means?

$A \cup B$ represents the union of the sets $A$ and $B$.

Q: What is the formula for union of sets?

The formula for the union of sets is $n(A \cup B)=n(A) + n(B) -n(A \cap B)$

Q: Can the union of two sets contain duplicate elements?

No, the union of sets cannot contain duplicate elements. Each element appears only once in the resulting set, even if it was present in both original sets.

Q: Is the union of a set with itself just the original set?

Yes, the union of a set with itself is the original set. For any set A, A ∪ A = A. This is known as the idempotent property of union.

Q: What is the union of a set with an empty set?

The union of any set A with an empty set ∅ is the set A itself. Mathematically, A ∪ ∅ = A. The empty set doesn't add any new elements to the union.

Q: Can the union of two non-empty sets be an empty set?

No, the union of two non-empty sets cannot be an empty set. Since union includes all elements from both sets, it will contain at least the elements from one of the non-empty sets.

Q: What is the commutative property of union?

The commutative property of union states that the order of sets doesn't matter when taking their union. For any sets A and B, A ∪ B = B ∪ A.

Union of sets, Properties of union

Edited By Komal Miglani | Updated on Jul 21, 2025 11:37 AM IST

Consider two sets : the set of all students scoring above 50% and the set of all students scoring below 51%. When combined, we get the set of all students in the class. This process of combining two or more sets without duplication is called the union of the sets. In real life, a set of books in a library is the union of sets of books in different genres like mystery, non-fiction, etc.

This Story also Contains

Union of Sets Definition
A Union B Formula
Formula for Number of Elements in A union B
Properties of the Union of Sets
Union of Sets Questions with Solutions
List of Topics Related to the Union of Sets
NCERT Resources
Practice Questions on Union of Sets

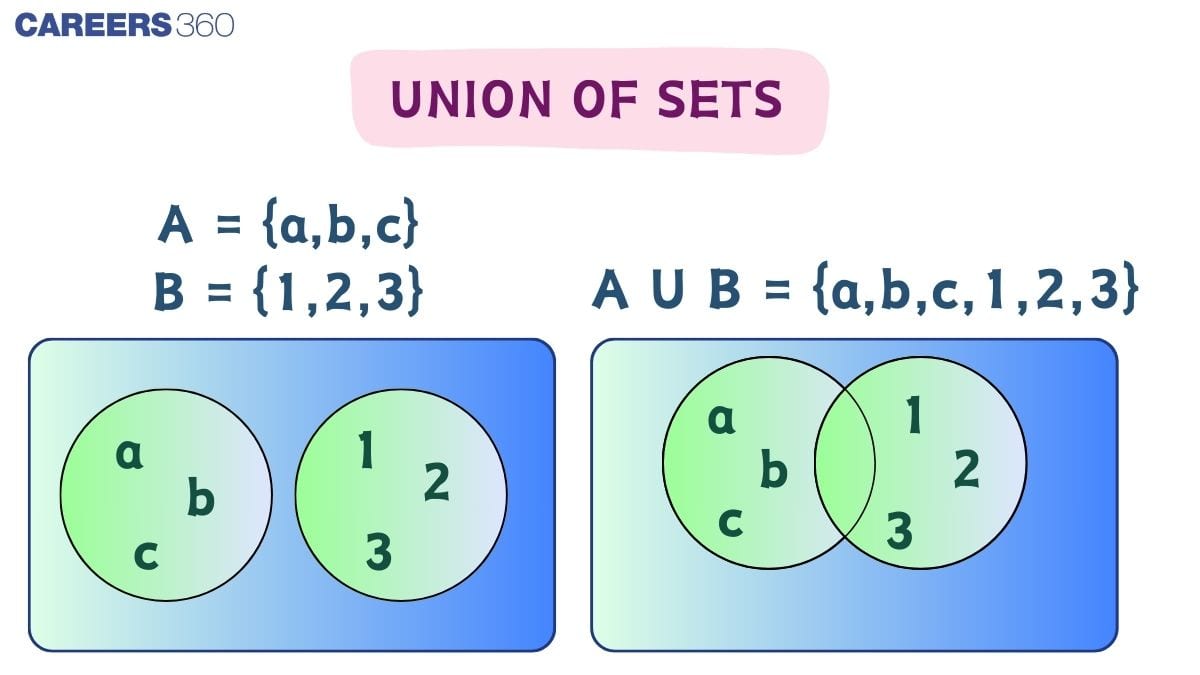
Union of sets, Properties of union

The concept of union of sets is an important topic under the chapter of Sets. In this article, we will look at definitions, formulas, important properties and some solved examples.

Union of Sets Definition

A set is simply a collection of distinct objects, considered as a whole. These objects, called elements or members of the set, can be anything: numbers, people, letters, etc. Sets are particularly useful in defining and working with groups of objects that share common properties.

Union of sets represents the combination of all elements of two or more sets.

Let $A$ and $B$ be any two sets. The union of sets $A$ and $B$ is the set that combines the elements in both sets without duplication. In other words, the union includes every distinct element that belongs to either $A$ or $B$.

Notation of the Union of Sets

Specific symbols are used to represent different operations. The symbol used for the union of two sets is ‘$\cup$’, which stands for union. This is known as infix notation, meaning the symbol is placed between the two sets involved in the operation.

Symbolically, we write $A \cup B=\{x: x \in A$ or $x \in B\}$.

This means any element that is a member of set $A$, set $B$, or both will be included in the resulting set $A \cup B$.

Union of Sets Examples

1. If $A=\{1,3,5,7\}$ and $B=\{2,4,6,8\}$ then $A \cup B$ is read as $A$ union $B$ and its value is, $A \cup B=\{1,2,3,4,5,6,7,8\}$

2. If If $A=\{d, e, g, y, c\}$ and $B=\{a,s,d,f\}$ then $A \cup B=\{a,c,d,e,f,g,s,y\}$

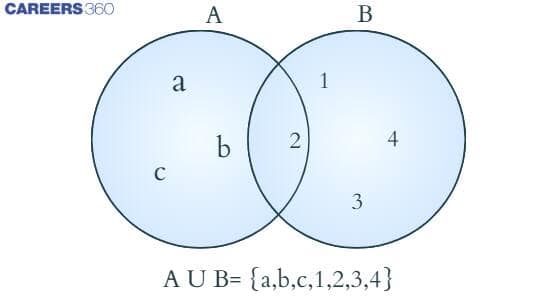
Union of Sets Venn Diagram

Let $A$ and $B$ be any two sets. The union of sets $A$ and $B$ is the set that combines the elements in both sets without duplication. The union of sets is denoted by '$\cup$ '.

Symbolically, we write $\mathrm{A} \cup \mathrm{B}=\{\mathrm{x}: \mathrm{x} \in \mathrm{A}$ or $\mathrm{x} \in \mathrm{B}\}$.

The venn diagram of union of sets is

A Union B Formula

The union of sets A and B refers to a set that includes all elements that are in A, in B, or in both. It is written as $A \cup B$ and is read as ”A union B” or ”A or B.” This formula is used to find the combined elements of sets A and B, without repeating any element.

Mathematically, the union of A and B is defined as: $A \cup B=\{x: x \in A$ or $x \in B\}$.

Formula for Number of Elements in A union B

Consider two sets, A and B, To determine the cardinal number of the union of these sets, we say

$n(A \cup B) = n(A) + n(B) - n(A \cap B)$

Here,

$n(A \cup B)$ = Total number of elements in $A \cup B$.

$n(A)$ = Number of elements in $A$.

$n(B)$ = Number of elements in $B$.

$n(A \cap B)$ = The number of elements that are common to both $A$ and $B$ also called the cardinality of set $A \cap B$, i.e. $A$ intersection $B$

Properties of the Union of Sets

1. Commutative Property: This signifies that the union of sets is independent of interchangeable properties.

$A \cup B=B \cup A$

2. Associative Property: This signifies that the union of three sets can be interchangeable.

$(A \cup B) \cup C=A \cup(B \cup C)$

3. Law of identity element: When we take the union of a finite set from a null set, the original set comes ( $\varphi$ is the identity of Null Set).

$\mathrm{A} \cup \varphi=\mathrm{A}$

4. Idempotent Property: This signifies that the union of the same set is itself.

$A \cup A=A$

5. Property of universal set: When we take union from a universal set then a universal set will come.

$U \cup A=U$

Note: If $A$ is a subset of $B$, then $A \cup B=B$

6. The union of any two sets results in a completely new set that contains the elements present in both the initial sets.

7. The resultant set contains all elements present in the first set, the second set, or elements in both sets.

8. The union of two disjoint sets results in a set that includes elements of both sets.

9. According to the commutative property of the union, the order of the sets considered does not affect the resultant set.

10. Cardinality of Union of two sets is always less than or equal to to the sum of cardinality of the two sets themselves.

$n(A \cup B)$ $<=n(A)+n(B)$

Union of Sets Questions with Solutions

Question 1: If set $\mathrm{A}=\{1,3,5\}$ and $\mathrm{B}=\{3,5,7\}$. Also $P=A \cup B$ and $Q=B \cup A$. Then which of the following is true?
1) $P=Q$
2) $P \subset Q$
3) $P \neq Q$
4) $Q \subset P$

Solution
In this Question,
As $A \cup B=B \cup A$
So, $P=Q$.
Hence, the answer is option 1.

Question 2: If $A=\{5,6,7\}$ and $B=\{\}$, then the value of $A \cup B$ is
1) { }
2) $\phi$
3) $\{5,6,7\}$
4) $\{5\}$

Solution
$\mathrm{A} \cup \varphi=\mathrm{A}$
Using this property, the union in this question will be $\{5,6,7\}$.
Hence, the answer is option 3.

Question 3 : What is the union of set A = {1,2,3,4} with a set $B=\left\{x: x^2-5 x+6=0\right.$ or $\left.x^2-5 x+4=0\right\}$?

1) $U$
2) $B$
3) None of these
4) Both (1) and (2)

Solution

$\begin{aligned} & B=\left\{x: x^2-5 x+6=0 \text { or } x^2-5 x+4=0\right\} \\ & x^2-5 x+6=0 \Rightarrow x=2,3 \\ & x^2-5 x+4=0 \Rightarrow x=1,4 \\ & \Rightarrow B=\{1,2,3,4\}\end{aligned}$

Thus $A = B$

Thus $A \cup B=A=B$

Hence, the answer is option 3.

Question 4: If $\mathrm{n}(\mathrm{U})=20, \mathrm{n}(\mathrm{A})=12, \mathrm{n}(\mathrm{B})=9, n(A \cap B)=4$ where U is the universal set, then $n(A \cup B)^c=$

Solution

$ \begin{aligned} & n(A \cup B)=n(A)+n(B)-n(A \cap B)=12+9-4=17 \\ & n(A \cup B)^{\prime}=n(U)-n(A \cup B)=20-17=3 \end{aligned} $
Hence, the answer is 3.

Question 5: Find the union of the sets $\{3,7,9\},\{5,8,1\}$ and $\{2,8,3\}$.
1) $\{1,2,3,4,5,8,7,9\}$
2) $\{1,2,3,5,7,8,9\}$
3) $\{1,2,3,4,7,8,9\}$
4) $\{1,2,5,7,8,9\}$

Solution
The union of these three sets is the set containing all the elements in these three sets Option (2) is correct

Options (1) and (3) have 4, which is not present in any of the given sets.
Option (4) is missing 3.
Hence, the answer is option 2.

List of Topics Related to the Union of Sets

Roster and Set Builder Form of Sets	Power Set
Equal and Equivalent Sets	Intersection of Sets, Properties of Intersection
Empty Set	Difference of Set
Finite and Infinite Sets	Complement of a Set, Law of Complement, Property of Complement
Singleton Set	De-morgan's Laws

NCERT Resources

Explore essential NCERT class 11 study materials for Sets, with comprehensive solutions, concise revision notes, and curated exemplar problems. These resources are designed to enhance your conceptual clarity and prepare you effectively for board and competitive exams.

Practice Questions on Union of Sets

Mastering any mathematical concept comes through continuous practice. To help strengthen your understanding of the topic, we have given below some practice questions on Union of sets. They will test your knowledge of formulas, important properties and general application of knowledge.

Union of Set - Practice questions

You can practice the next topics of Sets below:

Intersection of Set Properties of Intersection - Practice Questions

Difference of Set - Practice Questions

Complement of A Set Law of Complement Property of Complement - Practice Questions

Cardinal Number of Some Sets - Practice Questions

De Morgans Laws - Practice Questions

Frequently Asked Questions (FAQs)

1. What is union of sets?

Let $A$ and $B$ be any two sets. The union of sets $A$ and $B$ is the set that combines the elements in both sets without duplication. The union of sets is denoted by '$\cup$ '.

2. What does $\cap$ and $\cup$ mean in math?

$\cap$ represents the intersection of two sets while $\cup$ represents the union of two sets.

3. What are the factors which determine the complement of a set?

The complement of a set simply means all elements having any relations to the universal set without contacting the elements of the given set.

4. What does $A \cup B$ means?

$A \cup B$ represents the union of the sets $A$ and $B$.

5. What is the formula for union of sets?

The formula for the union of sets is $n(A \cup B)=n(A) + n(B) -n(A \cap B)$

6. Can the union of two sets contain duplicate elements?

No, the union of sets cannot contain duplicate elements. Each element appears only once in the resulting set, even if it was present in both original sets.

7. Is the union of a set with itself just the original set?

Yes, the union of a set with itself is the original set. For any set A, A ∪ A = A. This is known as the idempotent property of union.

8. What is the union of a set with an empty set?

The union of any set A with an empty set ∅ is the set A itself. Mathematically, A ∪ ∅ = A. The empty set doesn't add any new elements to the union.

9. Can the union of two non-empty sets be an empty set?

No, the union of two non-empty sets cannot be an empty set. Since union includes all elements from both sets, it will contain at least the elements from one of the non-empty sets.

10. What is the commutative property of union?

The commutative property of union states that the order of sets doesn't matter when taking their union. For any sets A and B, A ∪ B = B ∪ A.

11. How do we denote the union of two sets A and B?

The union of sets A and B is denoted by A ∪ B. The symbol "∪" is read as "union."

12. What does A ∪ B mean in set theory?

A ∪ B represents all elements that belong to set A or set B (or both). It includes every element from both sets, but each element appears only once in the result.

13. What is the union of three or more sets?

The union of three or more sets includes all unique elements from all the sets. For sets A, B, and C, it's denoted as A ∪ B ∪ C and contains elements in at least one of A, B, or C.

14. What is the union of a set with its proper subset?

The union of a set with its proper subset is the original set itself. If B is a proper subset of A, then A ∪ B = A.

15. How does union relate to the concept of disjoint sets?

For disjoint sets A and B (sets with no common elements), |A ∪ B| = |A| + |B|. The number of elements in their union is simply the sum of their individual cardinalities.

16. How do you find the number of elements in the union of two sets?

To find the number of elements in A ∪ B, use the formula: |A ∪ B| = |A| + |B| - |A ∩ B|. This accounts for elements counted twice in A and B.

17. How does union relate to the concept of mutually exclusive events in probability?

For mutually exclusive events A and B, P(A ∪ B) = P(A) + P(B). This is because there's no overlap between the events, so we simply add their individual probabilities.

18. How does union relate to the concept of a universal set?

The union of a set A with its complement A' (with respect to a universal set U) is the universal set itself. Mathematically, A ∪ A' = U.

19. What is the associative property of union?

The associative property of union states that for sets A, B, and C, (A ∪ B) ∪ C = A ∪ (B ∪ C). This means we can group sets in any order when taking multiple unions.

20. How does the union operation relate to subsets?

If A is a subset of B, then A ∪ B = B. This is because B already contains all elements of A, so adding A to B doesn't introduce any new elements.

21. What is the union of sets?

The union of sets is the combination of all unique elements from two or more sets. It includes every element that appears in at least one of the sets, without repeating any elements.

22. What is the difference between union and sum of sets?

Union combines elements without repetition, while sum (or multiset union) allows repetitions. For example, {1,2} ∪ {2,3} = {1,2,3}, but the sum would be {1,2,2,3}.

23. What is the union of two intervals in real numbers?

The union of two intervals is the set of all numbers that belong to either interval. If the intervals overlap or are adjacent, the result is a single interval. Otherwise, it's the combination of two separate intervals.

24. What is the difference between union and intersection of sets?

Union (∪) includes all elements from both sets, while intersection (∩) includes only the elements common to both sets. Union is more inclusive, intersection is more restrictive.

25. What is the union of all elements of a family of sets?

The union of all elements of a family of sets F, denoted by ∪F or ∪{A : A ∈ F}, is the set of all elements that belong to at least one set in the family.

26. How does union relate to the concept of a partition of a set?

The union of all subsets in a partition of set A is equal to A. Partitions divide a set into non-overlapping subsets, and their union reconstructs the original set.

27. Can the union of two infinite sets be a finite set?

No, the union of two infinite sets is always an infinite set. The resulting set will contain at least as many elements as the larger of the two infinite sets.

28. How does union relate to the concept of a power set?

The union of all subsets in the power set of A is A itself. This means that combining all possible combinations of elements from A results in A.

29. How does union relate to the concept of a Venn diagram?

In a Venn diagram, the union of sets is represented by all regions covered by at least one of the sets. It includes overlapping and non-overlapping regions of the sets.

30. What is the union of a set with its power set?

The union of a set A with its power set P(A) is the power set P(A) itself. This is because A is already a member of its power set, so A ∪ P(A) = P(A).

31. What is the distributive property of union over intersection?

The distributive property of union over intersection states that A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) for any sets A, B, and C.

32. What is the identity element for the union operation?

The empty set ∅ is the identity element for union. For any set A, A ∪ ∅ = A. The empty set doesn't add any new elements to the union.

33. What is the relationship between union and set difference?

For sets A and B, A ∪ B = A ∪ (B \ A), where B \ A is the set difference. This means union can be expressed as the combination of one set and the unique elements of another.

34. How does union relate to the concept of a complement in set theory?

The union of a set A and its complement A' with respect to a universal set U is the universal set itself: A ∪ A' = U. This illustrates that A and A' together cover all possibilities.

35. How does union relate to the concept of a sigma-algebra in measure theory?

In a sigma-algebra, the union of any countable collection of sets in the algebra must also be in the algebra. This property ensures closure under countable unions.

36. What is the union of a set with its cartesian product with another set?

The union of a set A with its Cartesian product A × B is neither A nor A × B, but a new set containing all elements of A and all ordered pairs in A × B.

37. How does union relate to the concept of a topology?

In topology, a collection of subsets forms a topology if it's closed under arbitrary unions. This means the union of any collection of sets in the topology must also be in the topology.

38. What is the union of all cosets of a subgroup in group theory?

The union of all cosets of a subgroup H in a group G is the entire group G. This is because cosets partition the group, and their union reconstructs the whole group.

39. How does union relate to the concept of a Boolean algebra?

In Boolean algebra, union is one of the fundamental operations (along with intersection and complement) that satisfy certain axioms, including commutativity, associativity, and distributivity.

40. What is the union of a set with its set of subsets?

The union of a set A with its set of subsets (power set P(A)) is the power set P(A). This is because A is already an element of P(A), so A ∪ P(A) = P(A).

41. How does union relate to the concept of a metric space?

In a metric space, the union of open sets is always open. This property is fundamental in defining the topology induced by a metric.

42. What is the union of all proper subsets of a set?

The union of all proper subsets of a non-empty set A is A itself. This is because every element of A is in at least one proper subset of A.

43. How does union relate to the concept of a field in abstract algebra?

In field theory, the union operation isn't typically used. Instead, fields are defined using addition and multiplication operations that satisfy certain axioms.

44. What is the union of a set with its set of permutations?

The union of a set A with its set of permutations is the set of permutations itself. This is because each element of A is already present in at least one permutation.

45. How does union relate to the concept of a basis in linear algebra?

The union of different bases of a vector space V is not necessarily a basis for V. However, the union of the spans of these bases is the entire vector space V.