Equal and Equivalent Sets
Understanding equal and equivalent sets is a fundamental part of set theory. These concepts help us compare sets based on their elements and the number of elements they contain. In simple terms, equal sets have exactly the same elements, while equivalent sets have the same number of elements, regardless of what those elements are.
- Set
- What are equal and equivalent sets?
- Properties of Equal and Equivalent Sets
- Equal and Equivalent Sets Examples
This article covers the definition of equal and equivalent sets, explains the difference between equal and equivalent sets, and provides examples of equal and equivalent sets to clarify each concept. You'll also find a worksheet on equal and equivalent sets with answers to help in learning through practice. Whether you're asking what is equal and equivalent sets in mathematics or looking for equal and equivalent sets examples, this resource offers everything you need in one place.
Set
A set is a collection of distinct items grouped together. These items are called elements. For example, the set of even numbers less than 10 is written as $A = \{2, 4, 6, 8\}$. Sets are shown using curly braces $\{ \}$ and named with capital letters like $A$, $B$, or $C$. Elements shouldn’t repeat.
For example, $B = \{\text{apple}, \text{banana}, \text{mango}\}$ is a valid set of fruits. Sets are used to represent groups with common features.
What are equal and equivalent sets?
In set theory, it's common to compare two sets to check how similar they are. Sometimes, sets may look different but have something in common—like the same elements or the same number of elements. In the sections below, we’ll explore what makes two sets equal and what makes them equivalent, along with clear examples. You’ll understand how to identify and differentiate between equal and equivalent sets easily.
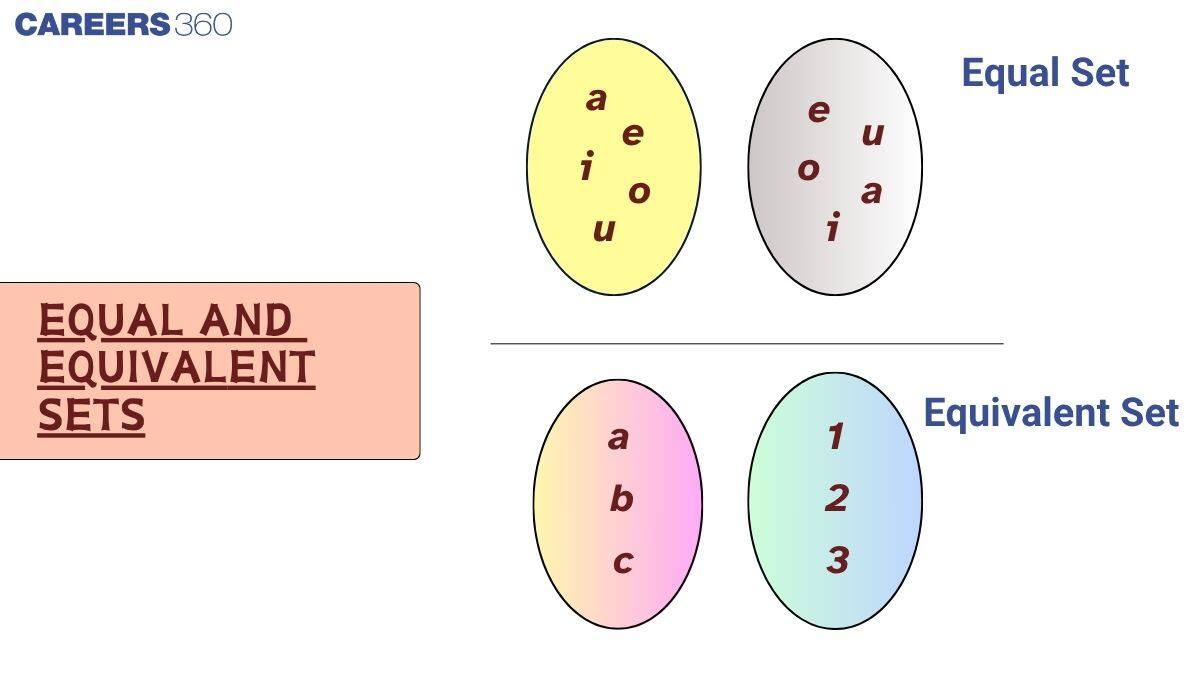
Equal Sets Definition
Two sets are called equal when they contain exactly the same elements, with no extra or missing items. The order of elements doesn't matter, but the content must be identical.
If $A = \{3, 2, 1, 4\}$ and $B = \{2, 3, 4, 1\}$, both sets have the same elements. So, we write $A = B$.
If even one element differs, the sets are not equal, and we write $A \neq B$.
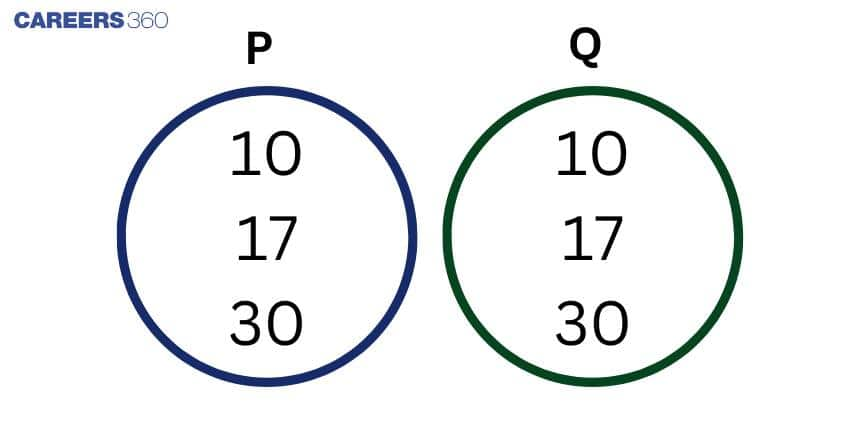
Equal Sets Representation Using Venn Diagram
Equal sets can be visually represented using a Venn diagram to show that both sets have exactly the same elements. When two sets are equal, their Venn diagram overlaps completely, indicating no difference in elements.
For example, if $P = \{10, 17, 30\}$ and $Q = \{10, 17, 30\}$, then both sets contain the same elements, and we write $P = Q$. In the Venn diagram, sets $P$ and $Q$ would completely overlap, showing they are identical.
Equivalent Sets Definition
Two sets are called equivalent if they have the same number of elements, even if the elements themselves are different. What matters is the count, not the content.
If $A = \{H, T, P, V\}$ and $B = \{1, 2, 3, 4\}$, both sets have 4 elements, so we say $A$ and $B$ are equivalent sets.
We write this as $n(A) = n(B)$, meaning both sets have equal cardinality.
Equivalent Sets Representation Using Venn Diagram
Equivalent sets can be shown using a Venn diagram to highlight that two sets have the same number of elements, even if the elements are different. Unlike equal sets, their elements don’t need to match—only the count matters.
For example, if $P = \{3, 6, 9\}$ and $Q = \{a, b, c\}$, both sets have three elements. So, $P$ and $Q$ are equivalent, and this can be represented by showing two separate but equally sized sets in a Venn diagram.
How do you check whether sets are equal or not?
When comparing, two sets, one has to check whether ' $A$ ' and ' $B$ ' are composed of the same elements or not. For example, set $A$ was defined as the set of $\{2,3,4\}$ and set $B$ was also defined as the set of $\{4,3,2\}$ and thus set $A$ and set $B$ are equal sets. Comparing two sets requires us to consider how many elements each set contains to come up with the conclusion that the two are equivalent.
Properties of Equal and Equivalent Sets
Equal and equivalent sets follow certain rules that help us identify and compare them accurately. These properties make it easier to understand how sets relate to each other based on their elements or size. Below, we’ll look at the key properties of equal and equivalent sets with simple explanations.
Properties | Equal Sets | Equivalent Sets |
1 | The order of elements does not affect equality. | Sets are equivalent if they have the same number of elements. |
2 | Equal sets must contain exactly the same elements. | The elements can be different; only the count matters. |
3 | All elements in both sets are equal. | Elements may or may not be the same. |
4 | Their cardinality (number of elements) is always equal. | Cardinality is also equal. |
5 | Two sets are equal if they are subsets of each other: $A \subseteq B$ and $B \subseteq A$. | Equivalent sets are not required to be subsets of each other. |
6 | All equal sets are also equivalent. | Equivalent sets are not always equal. |
7 | Equality is denoted by $A = B$. | Equivalence is denoted by $A \sim B$ or $A \equiv B$. |
8 | The symbol used to denote equal sets is '=' | The symbol used to denote equivalent sets is ~ or ≡ |
Equal and Equivalent Sets Examples
Understanding sets becomes easier with examples. Below are simple and clear examples of equal and equivalent sets to help you quickly grasp the difference between them based on their elements and count.
Example 1: Which of the following are equal sets?
1) $A=\{1,2,3,4\}$ and $B=$ collection of natural numbers less than 6
2) $A=\{$ prime numbers less than 6$\}$ and $B=\{$ prime factors of 30$\}$
3) $A=\{0\}$ and $B=\{x: x>15$ and $x<5\}$
Solution: In option (1), $A=\{1,2,3,4\}$ but $B=\{1,2,3,4,5\}$, hence not equal.
In option (2), $A=\{2,3,5\}$ but $B=\{2,3,5\}$, hence equal.
In option (3), $A=\{0\}$ but $B=$ Null set, hence not equal.
Hence, the answer is the option (2).
Example 2: Which of the following is NOT true?
1) Equivalent sets can be equal.
2) Equal sets are equivalent.
3) Equivalent sets are equal.
4) None of these
Solution: In this Question,
Equivalent sets may or may not be equal sets but equal sets always have the same number of elements and hence equal sets are always equivalent.
Hence, the answer is the option 3.
Example 3: Which of the following are equal sets?
1) $A_1$ is a set of letters of ALLOY and $B_1$ is a set of letters of LOYAL.
2) $A_2=\left\{n: n \in Z\right.$ and $\left.n^2 \leq 4\right\}$ and $B_2=\left\{n: n^2-3 n+2=0\right\}$
3) $A_3=\left\{x: x^2=9\right\}$ and $B_3=\{3\}$
4) $A_4=\{x: x$ is a vowel $\}$ and $B_4=\{\mathrm{a}, \mathrm{e}, \mathrm{i}, \mathrm{u}\}$
Solution: (1) $A_1=\{\mathrm{A}, \mathrm{L}, \mathrm{O}, \mathrm{Y}\}$, and $B_1=\{\mathrm{L}, \mathrm{O}, \mathrm{Y}, \mathrm{A}\}$, these are equal sets since they have exactly the same elements.
(2) $A_2=\{-2,-1,0,1,2\}, B_2=\{1,2\}$, so unequal.
(3) $A_3=\{3,-3\}, B_3=\{3\}$, so unequal.
(4) $A_4=\{a, e, i, o, u\}, B_4=\{a, e, i, u\}$, so unequal.
Hence, the answer is the option (1).
Example 4: Which of the following is not an empty set?
1) Real roots of $x^2+2 x+3=0$
2) imaginary roots of $x^2+3 x+2=0$
3) Real roots of $x^2+x+1=0$
4) Real roots of $x^4-1=0$
Solution: Option (1) has imaginary roots as Discriminant $<0$. So, there is no real root, and the set is empty.
Option (2) has real roots as Discriminant $>0$. So, there is no imaginary root, and the set is empty.
Option (3) has imaginary roots as Discriminant $<0$. So, there is no real root, and the set is empty.
Option (4): $x^4-1=0 \Rightarrow\left(x^2-1\right)\left(x^2+1\right)=0$, which gives $x= \pm 1$
Hence, it has 2 real roots. So, it is not empty.
So, the answer is the option 4.
Example 5: Which of the following are NOT equivalent sets?
1) $P=\{A, B, C, D, E\}$ and $Q=\{$ Jan,Feb,Mar,April,May $\}$
2) $P=\{x: x$ is a prime number on dice $\}$ and $Q=\{x: x$ is an even number on dice $\}$
3) $P=\left\{x: x \in R\right.$ and $\left.x^2-5 x+6=0\right\}$ and $Q=\left\{x: x \in R\right.$ and $\left.x^2-4 x+5=0\right\}$
4) $A=\{x: x$ is a vowel $\}$ and $B=\{x: x$ is a natural number less than 6$\}$
Solution: In (A), both sets have $5$ elements, hence they are equivalent.
In (B), $P=\{2,3,5\}$ and $Q=\{2,4,6\}$, hence equivalent.
In (C), $P$ has 2 elements as there are 2 roots of $x^2-5 x+6=0$ (as discriminant $>0$ ) but $x^2-4 x+5=0$ has no real roots (as discriminant $<0$ ), so $Q$ is empty, hence they are not equivalent.
In (D), both sets have $5$ elements, hence they are equivalent.
Hence, the answer is the option 3.
Practice Questions based Equal and Equivalent sets
Test your understanding with these quick MCQ-based practice questions on equal and equivalent sets. These are designed to help you identify key concepts and learn through simple, objective-type problems.
Equal And Equivalent Sets - Practice Question MCQ
To practice questions on the next topics covering subsets, finite sets, power sets, union and intersection of sets, check below:
NCERT Useful Resources
Find all the essential NCERT study materials for the chapter Sets in one place. This includes detailed notes, solved exemplar problems, and NCERT solutions covering important topics like types of sets, empty sets, set operations, Venn diagrams, and more—perfect for quick revision and concept clarity.
NCERT Maths Class 11 Chapter 1 Sets Notes
NCERT Maths Class 11 Chapter 1 Sets Solutions
NCERT Maths Exemplar Problems Class 11 Chapter 1 Sets
Recommended Video on Equal and Equivalent Sets
Watch this video for a quick and clear explanation of equal and equivalent sets with easy examples. It covers key definitions, differences, and examples to help you understand the topic better in just a few minutes.
Frequently Asked Questions (FAQs)
Equal sets can be defined as those sets that contain the same or equal elements as the other and they suggest that there is a one-to-one relationship in which each member of one of the sets is also a member of the other without duplication or omission of any element. Two sets having the same number of elements are called equivalent sets.
Example of equal and equivalent sets are as follows-
Equal set: Let $A$ be set of natural numbers and $B$ be set of whole numbers greater than $0$. $A = \{1,2,3,4,5,6....\}$ and $B = \{1,2,3,4,5,6,....\}$ have the same exact elements. So, the sets $A$ and $B$ are equal sets.
Equivalent set: Let $A$ be natural numbers less than $6$ and $B$ be whole numbers less than $5$. The cardinality of both sets $A$ and $B$ are equal. So, the sets $A$ and $B$ are equal.
Comparable set means that each element of one set can be paired with exactly one element of other set, and vice versa.
The difference between equal and equivalent sets can be stated as - sets are equal if all elements are equal in two or more sets whereas if the number of elements in two or more sets is the same, they are equivalent sets.
When comparing, two sets, one has to check whether ' $A$ ' and ' $B$ ' are composed of the same elements or not. For example, set $A$ was defined as the set of $\{2,3,4\}$ and set $B$ was also defined as the set of $\{4,3,2\}$ and thus set $A$ and set $B$ are equal sets. Comparing two sets requires us to consider how many elements each set contains to come up with the conclusion that the two are equivalent.
The cardinality of a set is the number of elements it contains. Two sets are equivalent if and only if they have the same cardinality. This means that equivalent sets have a one-to-one correspondence between their elements, even if the elements themselves are different.
Yes, equivalent sets can have different dimensions. For example, the set of points on a line (1-dimensional) can be equivalent to the set of points on a plane (2-dimensional) or in space (3-dimensional), as all these sets can have the same cardinality (e.g., the cardinality of the continuum).
Yes, sets with different mathematical properties can be equivalent as long as they have the same number of elements. For instance, the set of prime numbers less than 10 and the set of perfect squares less than 50 are equivalent (both have 4 elements) despite having very different mathematical properties.
For two sets to be equal, they must have the same number of elements (cardinality) and contain exactly the same elements. However, having the same number of elements is not sufficient for equality; the elements themselves must be identical.
In probability theory, equivalent sets (events) have the same number of outcomes and thus the same probability in a uniform probability space. This concept is crucial for understanding sample spaces and calculating probabilities of complex events.
Equal sets contain exactly the same elements, while equivalent sets have the same number of elements but may contain different items. For example, {1, 2, 3} and {1, 2, 3} are equal sets, while {1, 2, 3} and {a, b, c} are equivalent sets.
Yes, two sets can be equivalent but not equal. Equivalent sets have the same number of elements (cardinality) but may contain different items. For instance, {red, blue, green} and {apple, banana, orange} are equivalent (both have 3 elements) but not equal (they contain different items).
All equal sets are equivalent, but not all equivalent sets are equal. Equal sets have the same elements and thus the same number of elements, making them equivalent. However, equivalent sets may have different elements while still having the same number of elements.
Set equality refers to two sets having the same elements, while set identity refers to two variables or names referring to the exact same set object. In most contexts, equality and identity are treated the same for sets, but in some programming languages or mathematical formalisms, they might be distinguished.
Yes, infinite sets can be both equal and equivalent. Two infinite sets are equal if they contain exactly the same elements. They are equivalent if they have the same cardinality (size), even if their elements differ. For example, the set of all even integers is equivalent to the set of all integers, as both are countably infinite.
For two sets to be equal, they must be subsets of each other. In other words, if A and B are equal sets, then A is a subset of B, and B is a subset of A. This is often written as A ⊆ B and B ⊆ A, which implies A = B.
Yes, sets with different representations can be equal if they contain the same elements. For example, {x | x is a prime number less than 6} and {2, 3, 5} are equal sets, even though one is described by a rule and the other by listing its elements.
To prove that two sets A and B are equal, you need to show that every element in A is also in B (A ⊆ B) and every element in B is also in A (B ⊆ A). This is often done using a two-part proof: first proving A ⊆ B, then proving B ⊆ A.
The power set of a set A is the set of all subsets of A, including the empty set and A itself. If two sets are equal, their power sets will also be equal. Conversely, if the power sets of two sets are equal, the original sets must be equal.
Set equality applies to infinite sets in the same way as finite sets: two infinite sets are equal if they contain exactly the same elements. For example, the set of all even integers is equal to the set of all integers multiplied by 2, even though both sets are infinite.
Two sets are equal if they contain exactly the same elements, regardless of the order. To determine equality, check if every element in one set is also in the other set, and vice versa. If this is true for all elements, the sets are equal.
The symbol used to denote equal sets is "=". For example, if set A = {1, 2, 3} and set B = {3, 2, 1}, we write A = B to show that these sets are equal.
Yes, all empty sets are considered equal to each other. Since an empty set contains no elements, any two empty sets will always have the same (zero) elements, making them equal by definition.
The order of elements does not affect set equality. Sets {1, 2, 3} and {3, 2, 1} are equal because they contain the same elements, regardless of their order. This is because sets are defined by their elements, not by the arrangement of those elements.
In set notation, equal sets are represented using the equality symbol (=). For example, if A = {1, 2, 3} and B = {3, 2, 1}, we write A = B to show that these sets are equal.
The symbol used to denote equivalent sets is "≡". For example, if set A = {1, 2, 3} and set B = {a, b, c}, we write A ≡ B to show that these sets are equivalent (have the same number of elements).
Yes, sets with different data types can be equivalent as long as they have the same number of elements. For example, {1, 2, 3} (integers) and {"apple", "banana", "cherry"} (strings) are equivalent sets because they both have three elements.
One-to-one correspondence is a way to show that two sets are equivalent. It means that each element in one set can be paired with exactly one element in the other set, with no elements left unpaired. This demonstrates that the sets have the same number of elements, even if those elements are different.
A bijection is a one-to-one correspondence between two sets. If a bijection exists between two sets, they are equivalent. This means that each element in one set can be paired with exactly one element in the other set, and vice versa, demonstrating that the sets have the same number of elements.
Yes, equivalent sets can have different properties while still having the same number of elements. For example, {1, 2, 3} and {4, 5, 6} are equivalent (both have 3 elements), but their sums, products, and other properties may differ.
Yes, sets with different descriptions can be equal if they contain the same elements. For example, {x | x is an even prime number} and {2} are equal sets, even though they are described differently.
The empty set plays a unique role in set theory. All empty sets are equal to each other, as they all contain no elements. The empty set is equivalent only to itself, as no other set has zero elements. It's often denoted as {} or ∅.
Set equality is preserved under set operations. If A = B, then:
In computer science and programming, set equality often involves comparing the elements of two sets to ensure they contain the same items, regardless of order. Many programming languages provide built-in methods or functions to check for set equality, which typically involve comparing the elements of both sets.
Two sets are equivalent if and only if there exists a one-to-one (injective) function from one set to the other that is also onto (surjective), i.e., a bijective function. This bijection establishes a one-to-one correspondence between the elements of the two sets, proving their equivalence.
Two sets described using set-builder notation are equal if they define exactly the same elements. For example, {x | x is a prime number less than 10} = {2, 3, 5, 7}. The equality holds because both notations describe the same set of elements.
The principle of extensionality in set theory states that two sets are equal if and only if they have exactly the same elements. This principle is fundamental to the concept of set equality and emphasizes that sets are defined solely by their elements, not by how they are described or constructed.
For multisets (sets that can contain multiple instances of the same element), equality requires not only the same elements but also the same number of occurrences of each element. For example, {a, a, b} and {a, b, a} are equal multisets, but {a, a, b} and {a, b, b} are not.
Yes, sets with different algebraic structures can be equivalent if they have the same number of elements. For example, the set of integers modulo 4 under addition and the Klein four-group under multiplication are equivalent sets (both have 4 elements) despite having different algebraic structures.
In Venn diagrams, equal sets are represented by completely overlapping circles or regions. This visual representation helps illustrate that equal sets contain exactly the same elements, with no elements outside the overlap.
Equivalent sets have the same cardinal number, which represents the size or number of elements in the set. Cardinal numbers allow us to compare the sizes of sets, even infinite ones, without listing all their elements. Two sets are equivalent if and only if they have the same cardinal number.
In fuzzy set theory, two fuzzy sets are considered equal if they have the same membership function. This means that for every element in the universe of discourse, both fuzzy sets assign the same degree of membership, which can be any value between 0 and 1.
Yes, sets with different topological properties can be equivalent if they have the same cardinality. For example, the set of real numbers in the interval (0,1) is equivalent to the set of all real numbers, even though they have different topological properties (one is bounded, the other is not).
The axiom of extensionality in set theory states that two sets are equal if and only if they have the same elements. This axiom formalizes the intuitive notion of set equality and is fundamental to the development of set theory as a mathematical discipline.
In measure theory, equivalent sets (having the same cardinality) may have different measures. This concept is important in understanding the properties of various measures, such as Lebesgue measure, and in developing the theory of integration.
For ordered pairs and tuples, equality requires not only the same elements but also the same order. For example, (a,b) = (c,d) if and only if a=c and b=d. This is different from set equality, where order doesn't matter.
Yes, sets with different logical properties can be equivalent if they have the same number of elements. For example, the set of true statements in a logical system and the set of false statements could be equivalent, even though their logical properties are opposite.
The law of identity in logic, which states that each thing is identical to itself (A = A), is closely related to set equality. In set theory, this law manifests as the reflexive property of set equality: every set is equal to itself.
In abstract algebra, two algebraic structures are isomorphic if there exists a structure-preserving bijection between them. The underlying sets of isomorphic structures are always equivalent (have the same cardinality), but equivalent sets don't necessarily form isomorphic structures.
Two infinite series or sequences are considered equal if they have the same terms in the same order. For the sets of terms of these sequences to be equal, they must contain exactly the same elements, regardless of order. This distinction is important in analysis and set theory.
Yes, sets with different geometric representations can be equivalent if they have the same number of points. For example, the set of points on a circle is equivalent to the set of points on a line segment, as both have the cardinality of the continuum.
The axiom of choice is independent of the concept of set equality, but it has implications for comparing infinite sets. With the axiom of choice, we can establish bijections between certain infinite sets, proving their equivalence even when it's not intuitively obvious.
In category theory, equivalent sets correspond to isomorphic objects in the category of sets. This concept generalizes to other categories, where isomorphic objects play a role analogous to equivalent sets in set theory.
Two functions are equal if and only if their graphs (sets of ordered pairs) are equal. This means that for every input, both functions must produce the same output. The concept of set equality thus provides a rigorous way to define function equality.
Yes, sets with different physical interpretations can be equivalent if they have the same number of elements. For example, the set of electrons in an atom and the set of protons in another atom could be equivalent sets, despite representing different physical entities.
Also Read
21 Jul'25 11:37 AM
02 Jul'25 07:43 PM
02 Jul'25 07:42 PM
02 Jul'25 06:39 PM
02 Jul'25 06:39 PM
02 Jul'25 06:38 PM
02 Jul'25 06:38 PM
02 Jul'25 06:38 PM
02 Jul'25 06:38 PM
02 Jul'25 06:38 PM