Angular Momentum - Rotation About Fixed Axis
Angular Momentum - Firstly, Any object that has mass has momentum along with it. Momentum is defined as a product of the mass and velocity of a particular object. The difference between momentum and angular momentum is that momentum deals only with moving objects while angular momentum deals with rotating and spinning objects as well. In physical terms, Angular Momentum is defined as the property of any rotating object given by the product of the moment of inertia and angular velocity of the particular rotating object. Angular momentum is a vector quantity and is denoted by L. Angular Momentum is an important topic in the study of celestial objects.
This Story also Contains
- Units and Dimensions
- Angular Momentum Formula
- Derivation of Angular Momentum
- Angular Momentum of an Object about Fixed axis
Units and Dimensions
Angular Momentum is a conserved and extensive quantity. The conserved quantity defines that the values of the function remain constant along a specific trajectory of the system and the term extensive quantity defines that the magnitude of the object is dependent on the size of the system.
The Dimensions of Angular Momentum are M L2 T −1
The System of International (SI) Unit is kg m2 s−1
Angular Momentum Formula
The formula of Angular Momentum can be categorized in two situations,
Point Object
Extended Object
Point Object: The object that is accelerating around a fixed point is called Point Object.
Formula: L = r * p
Here, L is the angular momentum.
r is the radius that is between the object and the relatively fixed point.
p is the linear momentum.
It can also be given as the product between the mass (m) of the object and linear velocity (v) with respect to the fixed point,
L = mvrSin
Here, L = angular momentum
v = linear velocity of the object
m = mass of the object
Extended Object: The object that is rotating about a fixed point is called an Extended Object.
Formula: L = I * w
Here, L is the angular momentum
I is the rotational inertia
W is the angular velocity
The direction of the Angular Momentum can be given by the Right-Hand thumb rule such that the thumb directs towards the direction of angular momentum (L) as well as torque and angular velocity, and the fingers on the hand curl point towards the direction of rotation.
Derivation of Angular Momentum
We know that,
l = r × p,
When we differentiate the above formula with respect to the time we get,
\frac{dl}{dt}=\frac{d(r*p)}{dt}
![]()
By applying the product rule for differentiation,
\frac{d(r*p)}{dt}=(\frac{dp}{dt})*r+(\frac{dr}{dt})*p
![]()
Since, We know that the velocity is defined as the change in position at some time interval,
Hence, \frac{dr}{dt} and p = mv,
![]()
Thus, \frac{dr}{dt}*p = v * mv
![]()
Now, Since both the vectors are parallel to each other, their products shall be a zero. Now Consider, \frac{dp}{dt}*r
![]()
Since F = \frac{dp}{dt}
![]()
Thus, (\frac{dp}{dt} ) * r = F * r = τ
![]()
Hence it totally means that \frac{d(r×p)}{dt} = τ.
![]()
Since l= r×p, therefore,
\frac{dl}{dt} = τ
![]()
Angular Momentum of an Object about Fixed axis
The rate of change of total angular momentum with respect to time over a particular point is equivalent to the total net external torque acting on the system about the same point is stated as the angular momentum on a particle. Thus, the Angular Momentum remains conserved when the total external torque remains zero.
Now, We will understand the concept of angular momentum of a particle that performs rotational motion about a fixed axis, so as to calculate the net rate of change of angular momentum of a rotating object about a fixed axis.
Consider an object rotating about a fixed axis. Suppose a particle P in the body rotates about the axis as. For this system the total Angular momentum is given by,
r_{i} * p_{i}
![]()
Here,
p is the momentum that is equal to mv
r is the distance of the particle from the axis of rotation.
The total angular momentum towards an individual particle is given as l = r×p
Using the vector law of addition OP = OC + CP.
We can write the above derivation in the form, l = (OC +CP) * p = (OC * p) + (CP * p)
v=r_{p}w
![]()
Here,
rp is the perpendicular distance of point P from the axis of rotation.
Also, from the above equation, tangential velocity v at point p is perpendicular to the vector rp.
Now, using the right-hand thumb rule, the direction of the axis of rotation is parallel to the direction of product CP * v
Similarly, the product of the vectors OC×V is perpendicular to the axis of rotation.
So, we can write it as,
l = OC * mv +l_{z}
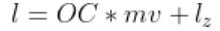
The component of angular momentum parallel to the fixed axis of rotation, which is along the z-axis is Iz
L = \Sigma l = \Sigma\left(l_{p} + l_{z}\right)
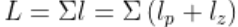
Here,
Lp is the perpendicular component of momentum and it can be given as,
L_{p} = \Sigma OC_{i} * m_{i}v_{i}
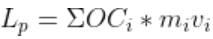
And Finally, the parallel component of the momentum is,
L_{z} = \left(\Sigma m_{i}r{^2_{i}}\right)\omega k'
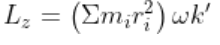
L_{z} = l_{z}\omega k'
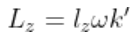
Each and every particle consisting of velocity vi has a particular particle that has velocity -vi accordingly pointed towards opposite on the circle, since the object is generally considered as symmetric about the axis of rotation. Thus, The total angular momentum of these particles cancels each other at a particular perpendicular distance rp.
The Total Momentum of a particular symmetrical object is given by,
L = L_{z} = l_{z}\omega k'
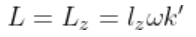
Frequently Asked Questions (FAQs)
Angular Momentum is directly proportional to the moment of inertia and it is a Vector quantity.
Fixed axis is a special case of rotational motion that defines the rotation around a fixed axis of a rigid body or surface.
Rotation of the Earth, Rotating fan blades, and Gyroscope are some basic examples of Angular momentum.
M L2 T −1 is the dimensional formula of Angular Momentum.
Angular momentum can be elaborated as the product of angular velocity and moment of inertia of an object.