Angular Momentum - Definition, Formula, Examples, FAQs

Momentum is the product of mass and velocity. It is a vector quantity. A closed system's momentum doesn't change unless an outside force is applied to it. Angular momentum is the characteristic that describes the rotatory inertia of an object in motion about an axis that may or may not pass through that particular object. The rotation and revolution of the Earth are among the best illustrations of angular momentum.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Definition of Angular Momentum
2. Solved Example Based on Angular Momentum
3. Summary

In this article, we will cover the concept of angular momentum. This topic falls under the broader category of rotational motion, which is a crucial chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), almost thirteen questions have been asked on this concept. And for NEET three questions were asked from this concept.

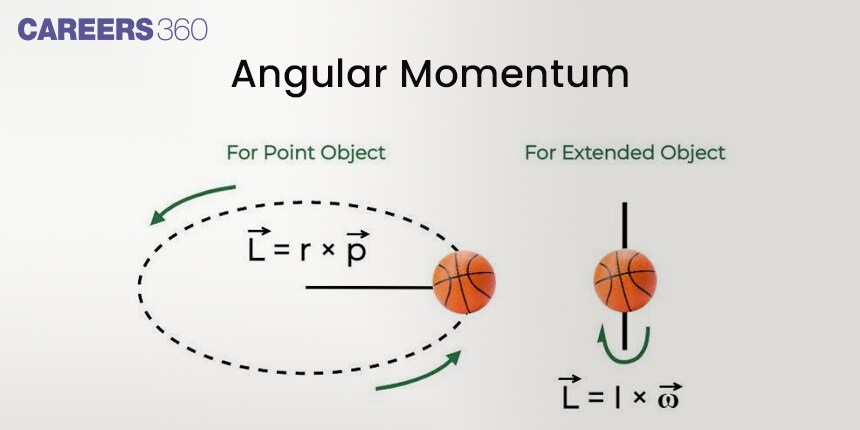
Let's read this entire article to gain an in-depth understanding of angular momentum.

Definition of Angular Momentum

The moment of linear momentum of a body with respect to any axis of rotation is known as angular momentum. If P is the linear momentum of a particle and its position vector from the point of rotation is r then angular momentum is given by the vector product of linear momentum and position vector.

$\begin{aligned}
& \vec{L}=\vec{r} \times \vec{P} \\
& \vec{L}=\vec{r} \times \vec{P}=\vec{r} \times(m \vec{V})=m(\vec{r} \times \vec{V})
\end{aligned}$

$|\vec{L}|=r p \sin \theta$, where $\theta$ is the angle between $\mathrm{r}$ and $\mathrm{p}$.
$
|\vec{L}|=m v r \sin \theta
$

Its direction is always perpendicular to the plane containing vector r and P and with the help of the right-hand screw rule, we can find it.

Its direction will be perpendicular to the plane of rotation and along the axis of rotation.

$
\begin{aligned}
& L_{\max }=r * P\left(\text { when } \theta=90^{\circ}\right) \\
& L_{\min }=0\left(\text { when } \theta=0^0\right)
\end{aligned}
$

SI Unit is Joule-sec or $\mathrm{kg}-\mathrm{m}^2 / \mathrm{s}$ Dimension $M L^2 T^{-1}$

In case of circular motion

As $\vec{r} \perp \vec{v}$ and $v=\omega r$ and $I=m r^2$
$
L=m v r=m r^2 \omega=I \omega
$

So in vector form $\vec{L}=I \vec{\omega}$

The net angular momentum of a system consisting of n particles is equal to the vector sum of the angular momentum of each particle.

$\vec{L}_{n e t}=\vec{L}_1+\vec{L}_2 \ldots \ldots .+\vec{L}_n$

Recommended Topic Video

Solved Example Based on Angular Momentum

Example 1: A particle of mass $m$ moves along line PC with velocity $\nu$ as shown. What is the angular momentum of the particle about $\mathrm{P}$ ?

1) $m \nu L$
2) $m \nu l$
3) $m \nu r$
4) zero

Solution:

Angular momentum

$
\vec{L}=\vec{r} \times \vec{p} \mid
$

The particle moves along the line PC.
$
\begin{aligned}
& \theta=0^{\circ} \\
& L=m v r \sin \theta^{\circ} \\
& \sin \theta^{\circ}=0 \\
& \mathrm{~L}=0
\end{aligned}
$

Hence, the answer is option (4).

Example 2: A particle of mass 2 kg is on a smooth horizontal table and moves in a circular path of radius 0.6 m. The height of the table from the ground is 0.8 m. If the angular speed of the particle is 12 rad s^-1, the magnitude (in kg m²s^-1) of its angular momentum about a point on the ground right under the centre of the circle is :

1) 8.64

2) 11.52

3) 14.4

4) 20.16

Solution:

We know,

$\vec{L}=\vec{r} \times \vec{p}$

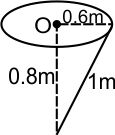
Angular momentum

$
\begin{aligned}
& L_0=m v r \sin \theta \\
& \theta=90^{\circ} \\
& L_0=m v r \sin 90^{\circ}
\end{aligned}
$

After calculation we get
$
L_0=14.4 \mathrm{~kg} \mathrm{~m}^2 / \mathrm{sec}
$

Hence, the answer is option (3).

Example 3: A ball of mass 160 g is thrown up at an angle of 60⁰ to the horizontal at a speed of 10 ms^-1. The angular momentum (in kg m²/s) of the ball at the highest point of the trajectory with respect to the point from which the .ball is thrown is nearly (g=10 ms^-2)

1) 1.73

2) 3

3) 3.46

4) 6

Solution:

$\begin{aligned} & (m v) L_{\perp} \\ & \text { Angular momentum about point } 0 \text { is }=\left(m u_x\right) H \\ & u_x=u / 2=5 \\ & H=\frac{u^2 \sin ^2 \theta}{2 g}=\frac{100 \times\left(\frac{\sqrt{3}}{2}\right)}{2 \times 10}=30 / 8=3.75 \mathrm{~m} \\ & \text { Angular momentum }=0.16 \times 5 \times 3.75 \mathrm{Kgm}^2 / \mathrm{s}=3.000 \mathrm{Kgm}^2 / \mathrm{s} \\ & \end{aligned}$

Example 4: A bob of mass m attached to an inextensible string of length l is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed rad/s about the vertical. About the point of suspension :

1) angular momentum is conserved.

2) angular momentum changes in magnitude but not in direction.

3) angular momentum changes in direction but not in magnitude.

4) angular momentum changes both in direction and magnitude.

Solution:

Angular momentum
$
\vec{L}=\vec{r} \times \vec{p}
$
wherein
$\vec{L}$ represent the angular momentum of a moving particle about a point.
it can be calculated as $L=r_1 P=r P_1$
$r_1=$ Length of perpendicular on the line of motion
$P_1=$ component of momentum along perpendicular to $r$

Angular momentum = mvr is constant as the distance of the bob from the point of suspensions and its speed both are constant.

The direction of angular momentum changes continually as shown in the figure

Example 5: A particle is moving in a circular path of radius a, with a constant velocity as shown in the figure. The centre of the circle is marked by ‘C’. The angular momentum from the origin O can be written as :

1) $v a(1+\cos 2 \theta)$
2) $v a(1+\cos \theta)$
3) va $\cos 2 \theta$
4) $v a$

Solution:

Angular momentum

$
\vec{L}=\vec{r} \times \vec{p}
$
wherein
$\vec{L}$ represent the angular momentum of a moving particle about a point.
it can be calculated as $L=r_1 P=r P_1$
$r_1=$ Length of perpendicular on the line of motion
$P_1=$ component of momentum along perpendicular to $r$

$\begin{aligned} & \cos \theta=\frac{a^2+L^2-a^2}{2 a L} \text { or } L=2 a \cos \theta \\ & \text { component of length } \perp^r \text { to velocity } \\ & =L \cos \theta \\ & =2 a \cos ^2 \theta \\ & \cos 2 \theta=2 \cos ^2 \theta-1 \\ & =2 \cos ^2 \theta=1+\cos 2 \theta \\ & L_{\perp}=a(1+\cos 2 \theta) \\ & \text { Angular momentum } L=m v L_{\perp}=m v a(1+\cos 2 \theta)\end{aligned}$

Summary

An object's angular momentum is represented by the equation or formula L = r⊥mv, which only changes when a net torque is applied. Thus, in the absence of torque, the object's perpendicular velocity will vary based on the radius, which is the separation between the body's mass centre and the circle's centre. It indicates that for shorter radii, velocity will be high and for longer radii, low.