Boltzmann Constant - Definition, Formula, Value, FAQs

History of the Invention of the Boltzmann Constant

The name Boltzmann constant was given the name after the Austrian researcher, Ludwig Boltzmann in the 19th century. Even though it was Ludwig first in the year 1877, who associated probability and entropy, in the black body radiation derivation initially in the 19th century, however, the association was not at all once indicated with a particular constant until Planck, invented the k and presented the most accurate value for it in the ordinance of the black body radiation derivation in the 19th century initially. Prior to the 19th century, calculations regarding the factors of Boltzmann were not put in writing applying the molecule per energy and the Boltzmann constant, instead applying a gas constant form, R and energy in macroscopy and quantities in macroscopy of the compound.

In the year 2017, the most precise calculations of the Boltzmann constant were acquired by gas thermometry which is acoustic, which represents the velocity of the volume of the monatomic gas in a chamber which is triaxial ellipsoid with applying resonances of acoustic and microwave. This time-consuming exertion was accepted with various experiments by many laboratories. It is one of the most well-received cornerstones of the year 2019 SI base unit redefinition. Based upon the calculations, the CODATA endorsed 1.380 649 × 10^-23 J.K^-1 to be the concluding Boltzmann constant value to be applied for the international system of the units.

What is the Boltzmann Constant?

The Boltzmann constant is a fundamental physical constant that relates the average kinetic energy of particles in a gas to the temperature of the gas. It acts as a bridge between the microscopic world (atoms and molecules) and the macroscopic world (temperature and energy).

It is denoted by the symbol $k_B$

The Formula of Boltzmann Constant

The formula of the Boltzmann constant relates the gas constant $(\mathbf{R})$ to Avogadro's number $\left(\mathbf{N}_a\right)$. It is given by:

$
k_B=\frac{R}{N_A}
$

where:

• $k_B=$ Boltzmann constant
• $R=$ Universal gas constant $=8.314 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}$
• $N_A=$ Avogadro's number $=6.022 \times 10^{23} \mathrm{~mol}^{-1}$

Value Of Boltzmann Constant

The value of the Boltzmann constant is:

$k=1.380649 \times 10^{-23} \mathrm{~J} \mathrm{~K}^{-1}$

Other Units:
In erg per kelvin (CGS system):

• $k=1.380649 \times 10^{-16} \mathrm{erg} \mathrm{~K}^{-1}$

In electronvolt per kelvin ( $\mathrm{eV} / \mathrm{K}$ ):

• $k=8.617333 \times 10^{-5} \mathrm{eV} \mathrm{~K}^{-1}$

Relation Between Boltzmann Constant and Gas Constant

Relation Between Boltzmann Constant and Gas Constant
The Boltzmann constant (k) and the gas constant (R) are related through Avogadro's number (NA).

The relation is given by the formula:

$
R=k \times N_A
$

Where,

• $R=$ Gas constant $=8.314 \mathrm{~J} / \mathrm{mol} \cdot \mathrm{K}$
• $k=$ Boltzmann constant $=1.38 \times 10^{-23} \mathrm{~J} / \mathrm{K}$
• $N_A=$ Avogadro's number $=6.022 \times 10^{23} \mathrm{~mol}^{-1}$

Boltzmann Constant Applications

The Boltzmann constant is very useful in many areas of physics. Some of its main applications are:
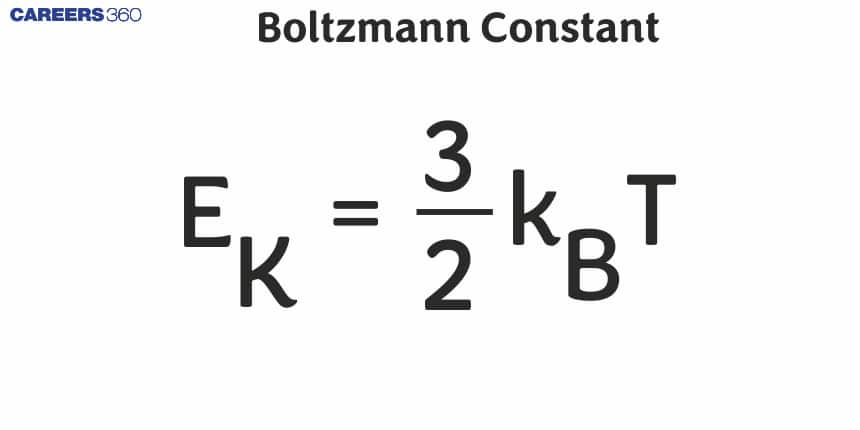
1. Kinetic Theory of Gases:

It relates the average energy of gas molecules to the temperature using the formula $E=\frac{3}{2} k T$.
2. Statistical Mechanics:

It helps to connect the behavior of individual atoms or molecules with the overall properties of matter.
3. Entropy Calculation:

It is used in the formula $S=k \ln W$ to find the entropy of a system.
4. Thermal Noise:

It is used to calculate the heat or noise produced in electrical circuits.
5. Blackbody Radiation:

It helps in studying how objects emit radiation depending on their temperature.

Summary

The Boltzmann constant was named after Ludwig Boltzmann. As the average kinetic energy of gas particles is connected to the temperature, it is a connection between microscopic and macroscopic physics. Defined as $1.380649 \times 10^{-23} \mathrm{~J} / \mathrm{K}$, it forms part of many equations in thermodynamics and is an important tool for understanding gas behaviour, entropy, and black-body radiation.