Dielectrics

Dielectrics, fundamental components in the realm of electromagnetism, are materials that insulate electric fields, allowing for the storage and manipulation of electrical energy. Unlike conductors, dielectrics do not permit the free flow of electric charge, which makes them crucial in a myriad of applications. In real life, dielectrics play a pivotal role in everyday technology—from the capacitors in your smartphone, which help manage power and maintain signal integrity, to the insulating layers in high-voltage power lines, ensuring safety and efficiency. In this article, we will understand dielectrics, we can better appreciate the sophisticated interplay between materials and electric fields that underpins much of modern technology.

This Story also Contains

1. Dielectric
2. Solved Examples Based On Dielectrics
3. Summary

Dielectric

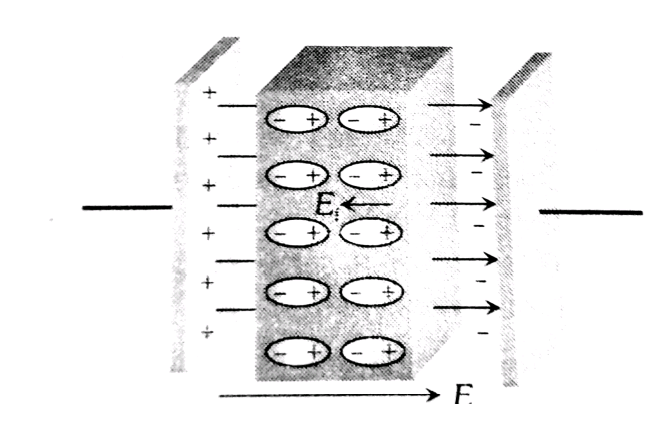
A dielectric is an insulating material in which all the electrons are tightly bound to the nuclei of the atoms and no free electrons are available for the conduction of current. They are non-conducting materials. They do not have free-charged particles like conductors have. They are of two types.

1. Polar: The centre of +ve and –ve charges do not coincide. For example HCl, ${\mathrm{H}}_2\mathrm{O}$, They have their own dipole moment

2. Non-Polar: The centres of +ve and –ve charges coincide. Example ${\mathrm{CO}}_2,{\mathrm{C}}_6{\mathrm{H}}_6$, They do not have their own dipole moment.

When a dielectric slab is exposed to an electric field, the two charges experience force in opposite directions. The molecules get elongated and develop a surface charge density ${\sigma }_p$. This leads to the development of an induced electric field Ep, which is in opposition direction of external electric field E_o. The net electric field E is given by $E=E_o-E_i$.

This indicates that the net electric field is decreased when the dielectric is introduced.

The ratio $\frac{E_0}{E}=K$ is called the dielectric constant of the dielectric. Hence, the Electric field inside a dielectric is $E_i=\frac{E_0}{K}$

$\begin{array}{rl}& E=E_0-E_i\text{and}E=\frac{E_0}{k}\\ & \text{So,}{E}_0-E_i=\frac{E_0}{K}\\ & \text{or}{E}_{0}K-E_{i}K=E_0\\ & \text{or}{E}_{0}K-E_0=E_{i}K\\ & \text{or}{E}_i=\frac{K-1}{K}{E}_0\\ & \text{or}\frac{{\sigma }_i}{{\epsilon }_0}\frac{K-1}{K}\frac{\sigma }{{\epsilon }_0}\\ & \text{or}{\sigma }_i=\frac{K-1}{K}\sigma \\ & \text{or}\frac{Q}{A}=\frac{K-1}{K}\frac{Q}{A}\\ & \text{or}{Q}_i=Q(1-\frac{1}{K})\end{array}$

This is irrespective of the thickness of the dielectric slab,i.e., whether it fills up the entire space between the charged plates or any part of it.

$C^{\prime }=\frac{{ϵ}_{0}A}{d-t+\frac{t}{k}}$

Recommended Topic Video

Solved Examples Based On Dielectrics

Example 1: The gap between the plates of a parallel plate capacitor of area A and the distance between plates d, is filled with a dielectric whose permittivity varies linearly from ${ϵ}_1$ at one plate to ${ϵ}_2$ at the other. The capacitance of a capacitor is :

1) ${ϵ}_0({ϵ}_1+{ϵ}_2)A/d$
2) ${ϵ}_0({ϵ}_2+{ϵ}_1)A/2d$
3) ${ϵ}_{0}A/[d\ln \left({ϵ}_2/{ϵ}_1\right)]$
4) ${ϵ}_0({ϵ}_2-{ϵ}_1)A/[d\ln \left({ϵ}_2/{ϵ}_1\right)]$

Solution:

As the permittivity of dielectric varies linearly from ${\epsilon }_1$ at one plate to ${\epsilon }_2$ at the other,

it is governed by an equation,$k=\left(\frac{{\epsilon }_2-{\epsilon }_1}{d}\right)x+{\epsilon }_1$

consider a small element of thickness dx at a distance x from the plate, Then,
$dV=\frac{E_o}{k}dx$
$\begin{array}{rl}& {\int }_0^{\mathrm{V}}\mathrm{dV}={\int }_0^{\mathrm{d}}\frac{\sigma }{{\epsilon }_0}\frac{1}{\left(\frac{{\epsilon }_2-{\epsilon }_1}{\mathrm{d}}\right)\mathrm{x}+{\epsilon }_1}\mathrm{dx}\\ & \mathrm{V}=\frac{\mathrm{d}\sigma }{{\epsilon }_0({\epsilon }_2-{\epsilon }_1)}\ln \left(\frac{{\epsilon }_2}{{\epsilon }_1}\right)\end{array}$
$\mathrm{Q}=\mathrm{CV}\Rightarrow \mathrm{C}=\frac{\mathrm{Q}}{\mathrm{V}}=\frac{\sigma \mathrm{A}}{\frac{\mathrm{d}\sigma }{{\epsilon }_0({\epsilon }_2-{\epsilon }_1)}\ln \left(\frac{{\epsilon }_2}{{\epsilon }_1}\right)}=\frac{{\epsilon }_0({\epsilon }_2-{\epsilon }_1)\mathrm{A}}{\mathrm{d}\ln \left(\frac{{\epsilon }_2}{{\epsilon }_1}\right)}$

Hence, the answer is the option (4).

Example 2: In polar materials, the dipole moment present in the absence of an electric field is

1)Zero

2)minimum

3)maximum

4)Infinite

Solution:

Polar Dielectric - The net dipole moment is zero in the absence of an electric field.

i.e ${\mathrm{CO}}_2,{\mathrm{NH}}_3,\mathrm{NCl}-\mathrm{etc}$

Hence, the answer is the option (1).

Example 3: A parallel plate capacitor of capacitance 90 pF is connected to a battery of emf 20 V. If a dielectric material of dielectric
constant $K=\frac{5}{3}$ is inserted between the plates, the magnitude of the induced charge will be :

1)0.9 nC

2)1.2 nC

3)0.3 nC

4)2.4 nC

Solution:

Polarisation of Dielectric slab

It is the process of inducing equal and opposite charges on the two faces of the dielectric.

wherein

$\begin{array}{rl}{Q}_{\text{ind}}=Q_f(1-& \frac{1}{K})\\ & =90\ast {10}^{-12}\ast 20\ast \frac{5}{3}(1-\frac{3}{5})\\ & =1200\ast {10}^{-12}\mathrm{C}\\ & =1.2nc\end{array}$.

Hence, the answer is the option (2).

Example 4: As shown in the figure, a very thin sheet of aluminium is placed in between the plates of the condenser. Then the capacity

1) Will increase

2) Will decrease

3) Remains unchanged

4) May increase or decrease

Solution:

If K filled between the plates

$$C^{\prime }=K\frac{{ϵ}_{0}A}{d}=C^{\prime }=Ck$$
wherein
$$\begin{array}{rl}& C\propto A\\ & C\propto \frac{1}{d}\end{array}$$

Since aluminium is a metal, therefore field inside this will be zero. Hence it would not affect the field between the two plates, so capacity q/v= q/Ed remains unchanged.

Hence, the answer is the option (3).

Example 5: When air in a capacitor is replaced by a medium of dielectric constant K, the capacity,

1) Decreases K times

2) Increases K times

3) Increases k² times

4) Remains constant

Solution:

Dielectric Constant (K)

$K=\frac{E}{E^{\prime }}$

wherein

K is also known as relative permittivity.

$C_{\text{medium}}=K\times C_{\text{air}}$

Hence, the answer is the option (2).

Summary

Dielectrics are insulating materials that do not conduct electricity but can transmit electric effects. They come in two types: polar and non-polar, and play a crucial role in various applications like capacitors. When exposed to an electric field, dielectrics develop an induced electric field that opposes the external field, reducing the net electric field. This behavior is quantified by the dielectric constant, which determines how much the capacitance of a capacitor increases when a dielectric is introduced.