Electric Potential Of Uniformly Charged Ring, Rod, And Disc

Wonder how electric potential is changing for differently shaped charged objects, like rings, rods, and disks? These geometries give rise to distinctive electric fields that shape the potential at a given point in their surroundings. We are going to see the electric potential coming from a uniformly charged object to understand the behaviour of their electric fields and their applications in design, starting from electronic components to the understanding of natural phenomena—the electric potential of a uniformly charged ring, rod, and disc—how they vary.

This Story also Contains

1. Electric Potential Due to Uniformly Charged Ring
2. Electric Potential due to uniformly charged Disc
3. Electric Potential due to a finite uniform line of charge-
4. Solved Examples Based On Electric Potential Of Uniformly Charged Ring, Rod, And Disc
5. Summary

This article is based on the concept of the Electric Potential Of a Uniformly Charged Ring, Rod, And Disc Which is important for competitive exams. This concept is included in the Electrostatics chapter in Class 12th physics. It is not only important for board exams but also important for JEE Main, NEET, and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of three questions have been asked on this concept.

Electric Potential Due to Uniformly Charged Ring

We want to find the electric potential at point P on the axis of the ring as of radius a, shown in the below figure

Total charge on ring: $Q$
Charge per unit length: $\lambda =Q/2\pi a$
Take a small elemental arc of charge dq
Charge on an arc: dq
So $dV=K\frac{dq}{r}=\frac{Kdq}{\sqrt{x^2+a^2}}$
$V(x)=K\int \frac{dq}{\sqrt{x^2+a^2}}=\frac{K}{\sqrt{x^2+a^2}}\int dq=\frac{KQ}{\sqrt{x^2+a^2}}$

• The potential at the centre of the ring

$V_c={\frac{KQ}{a}}_{(\text{since}\mathrm{x}=0)}$

• If x>>a

$V=\frac{KQ}{x}$

As x increases, V will decrease.
As $x\to \mathrm{\infty },V=0$.

So the maximum potential is at the centre of the ring.

Electric Potential due to uniformly charged Disc

We want to find the electric potential at point P on the axis of the disk of radius R, as shown in the below figure

Total charge on ring: $Q$
Charge per unit Area: $\lambda =Q/\pi R^2$

Take a small elemental with a ring of radius a having charge as dq

Area of ring: $2\pi ada$
Charge on ring: $dq=\sigma (2\pi ada)$
Charge on disk: $Q=\sigma \left(\pi R^2\right)$

$\begin{array}{rl}& dV=K\frac{dq}{\sqrt{x^2+a^2}}=2\pi \sigma K\frac{ada}{\sqrt{x^2+a^2}}\\ & V(x)=2\pi \sigma K{\int }_0^R\frac{ada}{\sqrt{x^2+a^2}}=2\pi \sigma K{\left[\sqrt{x^2+a^2}\right]}_0^R=2\pi \sigma K[\sqrt{x^2+R^2}-|x|]\end{array}$

We can also write

$V(x)=\frac{\sigma }{2{ϵ}_0}[\sqrt{x^2+R^2}-|x|]$

• The potential at the centre of the disc

$V_c={\frac{2KQ}{R}}_{\text{(since}\mathrm{x}=0)}$

• If x>>R

$\begin{array}{rl}& V(x)=2\pi \sigma K|x|[\sqrt{1+\frac{R^2}{x^2}}-1]\simeq 2\pi \sigma K|x|[1+\frac{R^2}{2x^2}-1]=\frac{K\sigma \pi R^2}{|x|}\\ & V(x)=\frac{KQ}{|x|}\end{array}$

As $|\mathrm{x}|$ increases, V will decrease.

$\text{As}|x|\to \mathrm{\infty },V=0$
So the maximum potential is at the centre of the disc.

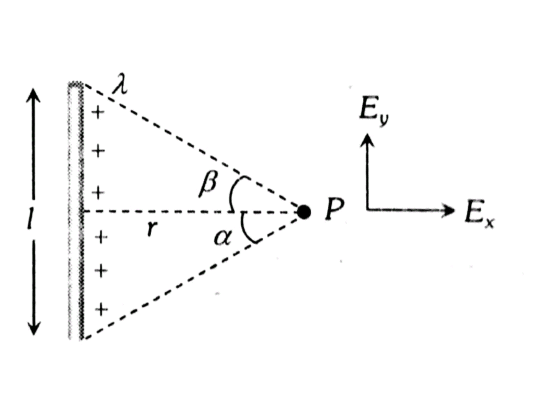
Electric Potential due to a finite uniform line of charge-

We want to find the potential due to a finite uniform line of positive charge at point P which is at a distance x from the rod on its perpendicular bisector, as shown in the below figure.

$\begin{array}{rl}& \lambda =\mathrm{Q}/2\mathrm{a}\text{Uniform linear charge density}\\ & \mathrm{dQ}=\lambda \mathrm{dy}\text{Charge in length dy}\\ & \mathrm{dV}=\mathrm{k}\frac{\mathrm{d}}{\mathrm{P}}\text{Potential of point charge}\\ & {\mathrm{V}}_{\mathrm{P}}={\int }_{-\mathrm{a}}^{+\mathrm{a}}\mathrm{dV}=\mathrm{k}\lambda {\int }_{-\mathrm{a}}^{+\mathrm{a}}\frac{\mathrm{dy}}{{({\mathrm{x}}^2+{\mathrm{y}}^2)}^{1/2}}\\ & \text{Using}\int \frac{dy}{{(x^2+y^2)}^{1/2}}=\ln [y+r]=\ln [y+{(x^2+y^2)}^{1/2}]\\ & {\mathbf{v}}_{\mathrm{P}}=\frac{\mathbf{k}\mathbf{Q}}{\mathbf{2}\mathbf{a}}\ln \left[\frac{{({\mathbf{x}}^2+{\mathbf{a}}^2)}^{1/2}+\mathbf{a}}{{({\mathbf{x}}^2+{\mathbf{a}}^2)}^{1/2}-\mathbf{a}}\right]\\ & \text{We get}\end{array}$

Recommended Topic Video

Solved Examples Based On Electric Potential Of Uniformly Charged Ring, Rod, And Disc

Example 1: A uniform non-conducting rod of mass $m$ and length $I$, with density $\lambda$ is hinged at the midpoint at the origin so that it can rotate in the horizontal plane. $\overrightarrow{E}$ is parallel to the x -axis in the entire region. Calculate time period of oscillation.

1) $2\pi \sqrt{\frac{m}{3\lambda }}$
2) $2\pi \sqrt{\frac{m}{3\lambda E}}$
3) $2\pi \sqrt{\frac{m}{\lambda }}$
4) $2\pi \sqrt{\frac{m\lambda }{3E}}$

Solution:

As we learned

Line Charge -

Electric field and Potential due to a charged straight wire length and charge density $\lambda$.

- wherein

$\begin{array}{rl}& \tau ={\int }_o^{\frac{1}{2}}d{\tau }_1+{\int }_o^{\frac{1}{2}}d{\tau }_2=2{\int }_o^{\frac{1}{2}}E\lambda dx(\sin \mathrm{\Theta }x)=\frac{E\lambda }{4}{l}^2\sin \mathrm{\Theta }\\ & \frac{M{l}^2}{12}\alpha =-\frac{E\lambda }{4}{l}^2\mathrm{\Theta }\Rightarrow T=2\pi \sqrt{\frac{m}{3E\lambda }}\end{array}$

Example 2: A charge particle $q$ is shifted from point 1 to 2 in electric feild due to staright long linear charge of $\lambda$, find the potential difference between 1 and 2 .

1) 0
2) $\mathrm{\infty }$
3) $\frac{\lambda }{2\pi {ϵ}_0}\ln 2$
4) $\frac{\lambda }{2\pi {ϵ}_{0}r}$

Solution:

As we have learnt,

Potential due to line charge -

$\begin{array}{rl}& V=\frac{\lambda }{2\pi {\epsilon }_0}{\log }_e\left[\frac{\sqrt{r^2+l^2}-l}{\sqrt{r^2+l^2}+l}\right]\\ & \mathrm{\Delta }V=\frac{W}{q}\\ & \Rightarrow w=\int F\cdot dr=q\int E\cdot dr=q\int \frac{\lambda }{2\pi {ϵ}_{0}r}\hat{r}\cdot dr\\ & =\frac{\lambda q}{2\pi {ϵ}_0}{\int }_R^{2R}\frac{dr}{r}=\frac{\lambda q}{2\pi {ϵ}_0}\ln 2\\ & \mathrm{\Delta }V=\frac{\frac{\lambda q}{2\pi {ϵ}_0}\ln 2}{q}=\frac{\lambda }{2\pi {ϵ}_0}\ln 2\end{array}$

Example 3: For a uniformly charged ring of radius R, the electric field on its axis has the largest magnitude at a distance h from its centre. Then value of h is:

1) $\frac{R}{\sqrt{5}}$
2) (correct)
$\frac{R}{\sqrt{2}}$
3) $R$
4) $R\sqrt{2}$

Solution:

The electric field due to the ring on its axis
$E_x=\frac{kQx}{{(x^2+R^2)}^{\frac{1}{2}}}$

here $x=h$

$E_h=\frac{kQh}{{(h^2+R^2)}^{\frac{1}{2}}}$
For finding maximum find $\frac{dE}{dh}$ and equate to zero

$\begin{array}{rl}& \Rightarrow kQ{(h^2+R^2)}^{\frac{3}{2}}=kQh\cdot \frac{3}{2}{(h^2+R^2)}^{\frac{1}{2}}\cdot 2h\\ & h^2+R^2=3h^2\\ & 2h^2=R^2\\ & h=\frac{R}{\sqrt{2}}\end{array}$

Example 4: A uniformly charged ring of radius 3a and total charge q is placed

in xy-plane centred at the origin. A point charge q is moving towards

the ring along the z-axis and has speed v at z=4a. The minimum

value of v such that it crosses the origin is :

$\begin{array}{rl}& \text{1)}\sqrt{\left(\frac{2}{m}\right)}{\left(\frac{4}{15}\frac{q^2}{4\pi {\epsilon }_{o}a}\right)}^{\frac{1}{2}}\\ & \text{2)}\sqrt{\left(\frac{2}{m}\right)}{\left(\frac{1}{5}\frac{q^2}{4\pi {\epsilon }_{o}a}\right)}^{\frac{1}{2}}\\ & \text{3)}\sqrt{\left(\frac{2}{m}\right)}{\left(\frac{2}{15}\frac{q^2}{4\pi {\epsilon }_{o}a}\right)}^{\frac{1}{2}}\\ & \text{4)}\sqrt{\left(\frac{2}{m}\right)}{\left(\frac{1}{15}\frac{q^2}{4\pi {\epsilon }_{o}a}\right)}^{\frac{1}{2}}\end{array}$

Solution:

$E$ and $V$ at a point $P$ that lies on the axis of the ring -

$E_x=\frac{kQx}{{(x^2+R^2)}^{\frac{3}{2}}}V=\frac{kQ}{{(x^2+R^2)}^{\frac{1}{2}}}$

Use energy conservation

$\begin{array}{rl}& \mathrm{\Delta }K\cdot E+\mathrm{\Delta }U=0\\ & 0-\frac{1}{2}m{v}^2=q(\frac{kq}{5a}-\frac{kq}{3a})\\ & \frac{1}{2}m{v}^2=\frac{2k{q}^2}{15a}\\ & v=\left(\frac{4}{15}\right)\left(\frac{k{q}^2}{am}\right)\\ & v=\sqrt{\frac{2}{m}}\times {(\frac{2}{15}\times \left(\frac{q^2}{4\pi {\epsilon }_o}\right)\times \frac{1}{a})}^{\frac{1}{2}}\end{array}$

Example 5: A conducting sphere of radius R= 20 cm is given a charge $Q=16\mu C$ . What is $\bar{E}$ at centre

Example 5: A conducting sphere of radius $\mathbf{R}=\mathbf{2}\mathbf{0}\mathbf{c}\mathbf{m}$ is given a charge $Q=16\mu \mathrm{C}$. What is $E$ at centre
1) $3.6\times {10}^6\mathrm{N}/\mathrm{C}$
2) $1.8\times {10}^6\mathrm{N}/\mathrm{C}$
3) Zero

4) None of the above

Solution:

As we learned

If $x\gg P$ -

$E=\frac{kQ}{x^2},V=\frac{kQ}{x}$

The electric field inside a conductor is always zero.

Summary

Electric potential for uniformly charged objects depends on the shape of the charge distribution and the distribution itself. For a ring, it is measured along its axis. For a rod, it varies linearly along and perpendicular to its length. Finally, the electric potential of a disc is usually explored along its central axis. It differs in mode of distribution, hence differing aspects of electric potential. These potentials are hence very important in the applications in Electronics, Physics, and Engineering where an electric field is required to be precisely controlled.