Spherical And Cylindrical Capacitors

Have you ever wondered about other ways in which electrical energy can be stored in a capacitor? The parallel plate capacitor is common, but there are many geometries for use in a number of applications. Two of them are the spherical and cylindrical capacitors which use the surfaces of a sphere and cylinder to store energy, each with its own set of advantages depending on the use. Spherical and cylindrical capacitor concepts help in designing more efficient and effective electronic devices.

This Story also Contains

1. Spherical capacitors
2. Cylindrical capacitor
3. Solved Examples Based On Spherical And Cylindrical Capacitors
4. Summary

Now this article read about the concept of Spherical And Cylindrical Capacitors. This concept is in the Class 12th physics electrostatic chapter. It is not only essential for board exams but also for competitive exams like the JEE Main, National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of five questions have been asked on this concept.

Spherical capacitors

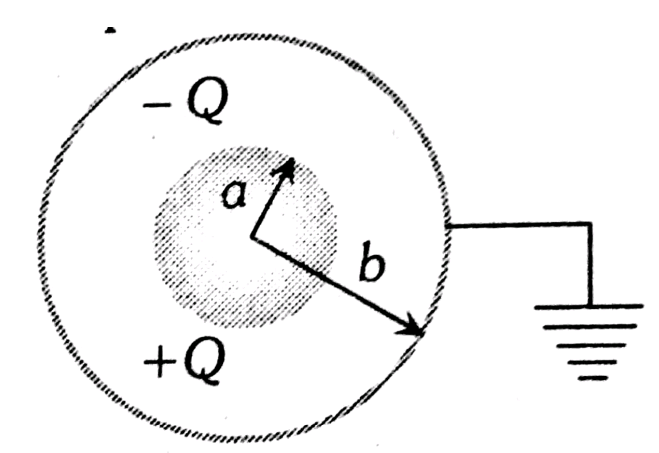
Spherical capacitors have two concentric spherical conducting shells of radii a and b, say b>a. The shell on the outer side is earthed. We place a charge +Q on the inner shell. It will reside on the outer surface of the shell. A charge -Q will be induced on the inner surface of the outer shell. A charge +Q will flow from the outer shell to the earth.

Consider a Gaussian spherical surface of radius r such that a<r<b.
From Gauss's law, the electric field at distance r>a is

$E=\frac{Q}{4 \pi \varepsilon_{0} r^{2}}$

The potential difference is :
$\begin{array}{l}{V_{b}-V_{a}=-\int_{0}^{b} \bar{E} \cdot d \bar{r}=-\int_{a}^{b} \frac{Q}{4 \pi \varepsilon_{0} r^{2}} d r} \\ \\ \text{Since } V_b =0, we\ have \\ {V_b=\frac{Q}{4 \pi \varepsilon_{0}}\left(\frac{1}{a}-\frac{1}{b}\right)=\frac{Q(b-a)}{4 \pi \varepsilon_{0} a b}} \\ \\ {\text { Therefore, capacitance, } C=\frac{Q}{V_{b}- V_{a}}=\frac{Q}{V_{a}}=\frac{4 \pi \varepsilon_{0} a b}{b-a}}\end{array}$

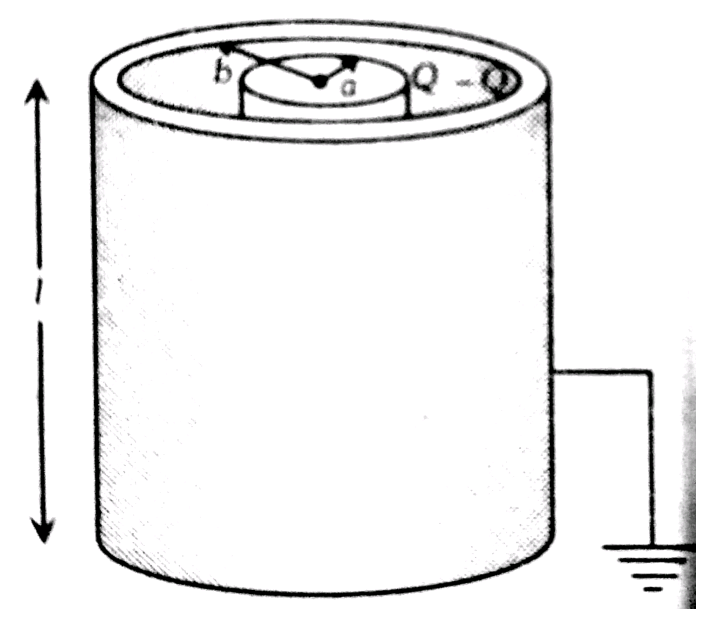
Cylindrical capacitor

It consists of two coaxial cylinders of radii a and b. Assume that b>a. The cylinders are long enough so that we can neglect the fringing of the electric field at the ends. The outer one is earthed. The electric field at a point between the cylinders will be radial and its magnitude will depend on the distance from the central axis. Consider a Gaussian surface of length y and radius r such that a<r<b. Flux through the plane surface is zero because the electric field and area vector are perpendicular to each other.

For the curved part,

$\begin{aligned} \phi &=\int \vec{E} \cdot d \vec{s}=\int E d s \\ &=E \int d s=E \cdot 2 \pi r y \end{aligned}$

Charge inside the Gaussian surface, $q=\frac{Qy}{L}$

From Gauss's law $\phi=E 2 \pi r y=\frac{Q y}{L \varepsilon_{0}} \Rightarrow E=\frac{Q}{2 \pi \varepsilon_{0} L r}$ .

Potential difference:

$\begin{aligned} V_{b}-V_{a}=-\int_{a}^{b} \bar{E} \cdot d \bar{r} &=-\int_{a}^{b} \frac{Q}{2 \pi \varepsilon_{0} L r} d r=-\frac{Q}{2 \pi \varepsilon_{0} L_{a}} \int_{a}^{b} \frac{1}{r} d r \\ \\ V_{a} &=\frac{Q}{2 \pi \varepsilon_{0} L} \ln \frac{b}{a} \quad\left(\text { since } V_{b}=0\right) \end{aligned}$

Therefore, the Capacitance of the cylindrical capacitor is,

$C=\frac{Q}{V_{\alpha}-V_{a}}=\frac{Q}{V_{a}}=\frac{2 \pi \varepsilon_{0} L}{\ln \left(\frac{b}{a}\right)}$

Recommended Topic Video

Solved Examples Based On Spherical And Cylindrical Capacitors

Example 1: A solid conducting sphere of radius R₁ is surrounded by another concentric hollow conducting sphere of radius R₂. The capacitance of this assembly is proportional to

1)$\frac{R_2-R_1}{R_1R_2}$

2)$\frac{R_2+R_1}{R_1R_2}$

3)$\frac{R_1R_2}{R_2+R_1}$

4)$\frac{R_1R_2}{R_2-R_1}$

Solution:

As we have learned

Spherical Capacitor -

It consists of two concentric spheres of radii a and b (a<b) inner sphere charges +Q while the outer sphere is earthed.

- wherein

CAPACITANCE OF THE GIVEN ASSEMBLY

$C= 4\pi\varepsilon _0\frac{R_1R_2}{R_2-R_1}\Rightarrow C\propto \frac{R_1R_2}{R_2-R_1}$

Example 2: Two spherical conductors each of capacity C are charged to potentials V and -V These are then connected using a fine wire. The loss of energy will be,

1)zero

2)$1/2 CV^2$

3)$CV^2$

4) $2 CV^2$

Solution:

The energy loss can be expressed as follows:

$\Delta U=\frac{C_1 C_2\left(V_1+V_2\right)^2}{2\left(C_1+C_2\right)}$

Here, ∆U is the energy loss due to the combining of capacitors.

Since the capacitance of both the capacitors is c, and the potential is v, the energy loss can be calculated as follows:

$\begin{gathered} \Delta U=\frac{C \times C \times(V+V)^2}{2(C+C)} \\ \Delta U=\frac{C^2 \times 4 V^2}{2 C} \\ \Delta U=2 C V^2 \end{gathered}$

Example 3: A spherical drop of capacitance 1 $\mu F$ is broken into eight drops of equal radius. Then, the capacitance of each small drop is

1) $1/8 \mu F$

2)$8 \mu F$

3) $1/2 \mu F$

4)$1/4 \mu F$

Solution:

As we have learned

Spherical Capacitor -

It consists of two concentric spheres of radii a and b (a<b) inner sphere charges +Q while the outer sphere is earthed.

- wherein

Using $C= n^{1/3}c\Rightarrow c= \frac{C}{n^{1/3}}= \frac{C}{8^{1/3}}= \frac{C}{2}= \frac{1}{2}\mu F$

Example 4: The intensity of the electric field at a point between the plates of a charged capacitor

1) Is directly proportional to the distance between the plates

2)Is inversely proportional to the distance between the plates

3)Is inversely proportional to the square of the distance between the plates

4) Does not depend on the distance between the plates

Solution:

As we have learned

If a dielectric is inserted between the sphere

${C}'=4\pi \epsilon _{0}k\frac{ab}{b-a}$

The electric field between the plates of the parallel plate capacitor is uniform and it doesn't depend upon distance.

Example 5: Capacitance of Cylindrical Capacitor is given by

1)$C= \frac{ab}{b-a}$

2)$C' = 4\pi \varepsilon _0\cdot \frac{b^2}{b-a}$

3)$4 \pi \varepsilon _0\cdot \frac{b^2}{b-a}= 4\pi \varepsilon _0\frac{ab}{b-a}+4\pi\varepsilon _0b$

4)$C= \frac{2\pi \varepsilon _0l }{log_e(\frac{b}{a})}$

Solution:

As we have learned

Cylindrical Capacitor -

$C=\frac{2\pi \epsilon _{0}l}{\log_{e}\left ( \frac{b}{a} \right )}$

- wherein

Summary

Spherical and cylindrical capacitors are useful capacitors composed so that a sphere and a cylinder help in storing electrical energy, respectively. For example, a spherical capacitor consists of two concentric spherical conductive shells separated by a dielectric material. A cylindrical capacitor consists of two coaxial cylindrical conductive shells surrounded by a dielectric. The capacitance of such capacitors depends on their geometric dimensions and the dielectric material used. They are found in special applications, where they are taken to be advantageous in the geometry they show—for instance, in coaxial cables and some types of sensors.