Kepler’s Laws Of Planetary Motion

Kepler’s Laws of Planetary Motion, formulated by the German astronomer Johannes Kepler in the early 17th century, revolutionized our understanding of the solar system by describing how planets orbit the Sun. These laws not only laid the foundation for modern astronomy but also provided insight into the predictable and harmonious nature of celestial movements. In real life, the principles behind Kepler's laws are observed in various scenarios, such as satellite orbits around Earth, which rely on the same gravitational forces that govern planetary motion. Even the rhythm of seasons and the timing of solar eclipses can be traced back to the precise mechanics described by Kepler, demonstrating how these ancient laws continue to shape our daily experiences.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Kepler's Law
2. Solved Examples Based on Kepler’s Laws of Planetary Motion
3. Summary

Kepler's Law

Kepler gives three empirical laws which govern the motion of the planets which are known as Kepler’s laws of planetary motion.

As we know planets are large natural bodies rotating around a star in definite orbits.

So, Kepler's laws are

(a) First Law (Law of Ellipses)
Each planet orbits the Sun in an elliptical path, with the Sun located at one of the two foci of the ellipse. This law explains why the distance between a planet and the Sun changes as the planet moves along its orbit.

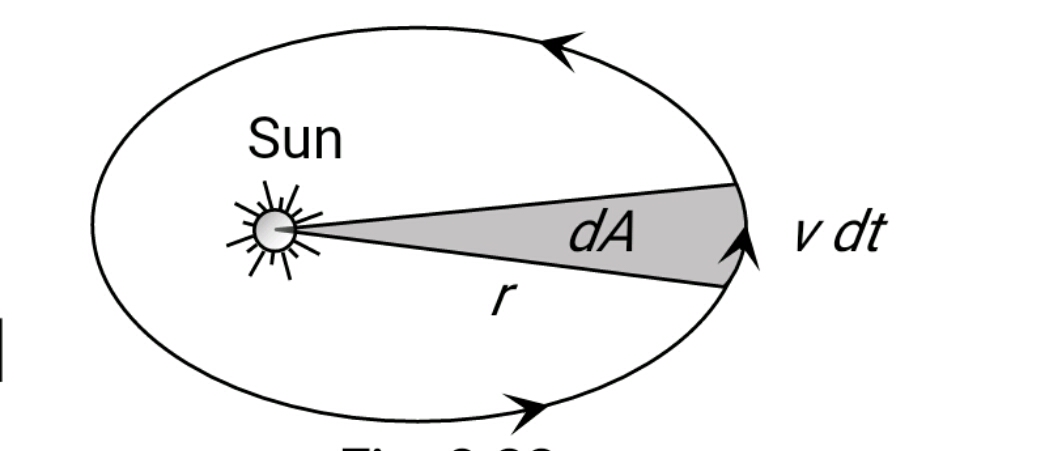
(b) Second Law (Law of Equal Areas)
A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. This means that a planet moves faster when it is closer to the Sun and slower when it is farther away, ensuring that the area covered over a given time period is the same.

The below figure

Area of velocity $=\frac{dA}{dt}$
$\frac{dA}{dt}=\frac{1}{2}\frac{(r)(Vdt)}{dt}=\frac{1}{2}rV$
Where
$\frac{dA}{dt}{\to }_{\text{Areal velocity}}$
$dA\to$ small area traced
Kepler's 2nd law is Similar to the Law of conservation of momentum
As $\frac{dA}{dt}=\frac{L}{2m}$
where
$L=mvr\to$ Angular momentum

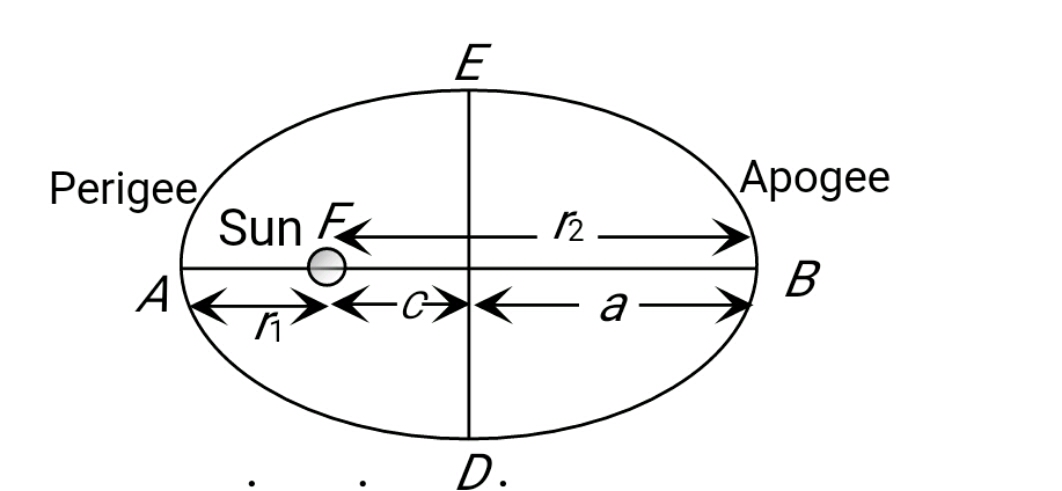
(c) The Law of Periods

The square of the orbital period of a planet (the time it takes to complete one orbit around the Sun) is directly proportional to the cube of the semi-major axis of its orbit (the average distance from the Sun)

The below figure

$$\begin{array}{rl}& AB=AF+FB\\ & 2a=r_1+r_2\\ & \therefore a=\frac{r_1+r_1}{2}\end{array}$$
Where
$a=$ semi-major Axis
$r_1=$ The shortest distance of the planet from the sun (perigee)
$r_2=$ The largest distance of the planet from the sun (apogee)
So if $\mathrm{T}=$ Time period of revolution
Then according to Kepler's 3rd law.

$$\begin{array}{rl}& T^2\alpha a^3\\ & \text{or}{T}^2\alpha {\left(\frac{r_1+r_2}{2}\right)}^3\end{array}$$

Recommended Topic Video

Solved Examples Based on Kepler’s Laws of Planetary Motion

Example 1: A planet moving around the sun sweeps area A₁ in 2 days A₂ in 3 days and A₃ in 6 days. Then the relation between A₁ ,A₂ and A₃ is

1) 3A₁ = 2 A₂ = A₃

2) 2 A₁ = 3 A₂ = 6 A₃

3) 3 A₁ = 2 A₂ = 6 A₃

4) 6 A₁ = 3 A₂ = 2 A₃

Solution:

According to Kepler's second law, the average velocity of the planet around the sun remains constant.

$\begin{array}{rl}& \frac{A_1}{t_1}=\frac{A_2}{t_2}=\frac{A_3}{t_3}\\ & \frac{A_1}{2}=\frac{A_2}{3}=\frac{A_3}{6}=3A_1=2A_2=A_3\end{array}$

Hence, the answer is the option (1).

Example 2: If the angular momentum of a planet of mass m, moving around the Sun in a circular orbit is L, about the centre of the Sun, its areal velocity is

1) $\frac{L}{m}$
2) $\frac{4L}{m}$
3) $\frac{L}{2m}$
4) $\frac{2L}{m}$

Solution:

Kepler's 2nd law

$\frac{dA}{dt}=\frac{1}{2}\frac{(r)(Vdt)}{dt}=\frac{1}{2}rV$

$\frac{dA}{dt}{\to }_{\text{Areal velocity}}$
$dA\to$ small area traced
wherein
Similar to the Law of conservation of momentum

$$\frac{dA}{dt}=\frac{L}{2m}$$

$L\to$ Angular momentum
it is also known as the Law of Area
So from the question

$$\begin{array}{rl}& \mathrm{dA}=\frac{1}{2}{r}^{2}d\theta \\ & \frac{dA}{dt}=\frac{1}{2}{r}^2\frac{d\theta }{dt}\\ & \frac{dA}{dt}=\frac{1}{2}{r}^2\omega \\ & \mathrm{L}={\mathrm{mr}}^2\omega \\ & \Rightarrow \frac{dA}{dt}=\frac{L}{2m}\end{array}$$

Hence, the answer is the option (3).

Example 3: Figure shows elliptical path abcd of a planet around the sun S such that the area of triangle csa is 1/4 the area of the ellipse. (See figure) With db as the semimajor axis, and ca as the semiminor axis. If t₁ is the time taken for the planet to go over path abc and t₂ for the path taken over cda then :

1) t₁ = t₂

2) t₁ = 2t₂

3) t₁ = 3t₂

4) t₁ = 4t₂

Solution:

Kepler's 3rd law

$$T^2\alpha a^3$$
From fig.

$$\begin{array}{rl}& AB=AF+FB\\ & 2a=r_1+r_2\\ & \therefore a=\frac{r_1+r_1}{2}\\ & a=\text{semi major Axis}\\ & r_1=\text{Perigee}\end{array}$$

wherein
Known as the law of periods

$$\begin{array}{rl}& r_2=\text{apogee}\\ & T^2\alpha {\left(\frac{r_1+r_2}{2}\right)}^3\\ & r_1+r_2=2a\\ & \frac{t_1}{t_2}=\frac{A/2+A/4}{A/2-A/4}=\frac{3A/4}{A/4}=3\\ & \therefore t_1=3t_2\end{array}$$

Hence, the answer is the option (3).

Example 4: India’s Mangalyan was sent to Mars by launching it into a transfer orbit EOM around the sun. It leaves the earth at E and meets Mars at M. If the semi-major axis of Earth’s orbit is a_e = 1.510¹¹ m, that of Mar’s orbit a_m = 2.2810¹¹ m, taken Kepler’s laws give the estimate of time for Mangalyan to reach Mars from Earth to be close to : (In days)

1) 260

2) 320

3) 500

4) 220

Solution:

Kepler's 3rd law

$$T^2\alpha a^3$$
From fig.

$$\therefore a=\frac{r_1+r_1}{2}$$

$a=$ semi major Axis
$r_1=$ Perigee

$$r_2=\text{apogee}$$
For EOM

$$\begin{array}{rl}{r}_m& =\frac{1.5+2.28}{2}=1.89\\ \frac{T_m}{T_e}& ={\left(\frac{1.89}{1.5}\right)}^{\frac{3}{2}}\Rightarrow >T_m=T_e\ast {\left(\frac{1.89}{1.5}\right)}^{\frac{3}{2}}\end{array}$$

time for Mangalyan to reach Mars from Earth=t= $=\frac{T_m}{2}$

$$\text{So}t=\frac{365}{2}\times 1.41=257.3\text{days}$$

Hence, the answer is the option (1).

Example 5: The time period of a satellite of Earth is 5 hours. If the separation between the earth and the satellite is increased to 4 times the previous value, the new time period will become ( In hours)

1) 40

2) 80

3) 10

4) 20

Solution:

Kepler's 3rd law

$$T^2\alpha a^3$$
From fig.

$$\begin{array}{rl}& AB=AF+FB\\ & 2a=r_1+r_2\\ & \therefore a=\frac{r_1+r_1}{2}\\ & a=\text{semi major Axis}\\ & r_1=\text{Perigee}\end{array}$$

wherein

$$\begin{array}{rl}& r_2=\text{apogee}\\ & T^2\alpha {\left(\frac{r_1+r_2}{2}\right)}^3\\ & r_1+r_2=2a\\ & T^2\propto r^3\\ & {\left(\frac{T_1}{T_2}\right)}^2={\left(\frac{r_1}{r_2}\right)}^3={\left(\frac{1}{4}\right)}^3\end{array}$$$\begin{array}{rl}& =\frac{1}{64}\\ & \frac{T_1}{T_2}=\frac{1}{8}\\ & \Rightarrow T_2=8T_1=40\mathrm{hrs}\end{array}$

Hence, the answer is the option (1).

Summary

Kepler's Laws of Planetary Motion provide a framework for understanding the elliptical orbits of planets, their varying speeds, and the relationship between their orbital periods and distances from the Sun. These laws are essential in predicting planetary motion, designing satellite orbits, and solving real-world problems, such as estimating travel times for space missions. By applying these principles, we gain insight into the predictable and harmonious patterns that govern celestial mechanics.