The Escape Velocity of Earth - Definition, Formula, FAQs

Edited By Vishal kumar | Updated on Sep 24, 2024 04:40 PM IST

Do you ever think of why the rockets are not pulled towards earth due to gravity meanwhile all other objects are pulled down by the gravitational force when they are thrown opposite to gravity? This is due to the velocity of the objects. When the velocity of the object is very much higher, then it can move against the gravitational force of the earth. This required velocity is known as the escape velocity. Every celestial body like natural satellites and planets have some minimum escape velocity to escape from the gravitational force or gravitational influence of the other celestial bodies in space. Let us define escape velocity by finding what is escape velocity or what is escape speed value and also compare the value of escape velocity of earth or escape speed of earth, escape velocity of moon, escape velocity of jupiter and escape velocity of sun. We can also see how velocity of earth escape velocity helps us in the rocket launching.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

Escape velocity definition:
The formula for escape velocity:
What is the escape velocity of earth?
Why this escape velocity is required?

The Escape Velocity of Earth - Definition, Formula, FAQs

Escape velocity definition:

The escape velocity definition can be given as the velocity with which the object or body travels without any break from the earth or moon against the gravitational pull and leave without any external population development.

Also read -

The formula for escape velocity:

At the escape velocity, the energy is conserved i.e. the gravitational potential energy will be equal to the kinetic energy. The sum of total energy will be equated to zero. The equation of escape velocity can be obtained by equating the gravitational potential energy of the object to the kinetic energy of the same object which is with a mass of m and velocity v associated with it. The expression for the escape velocity can be given as

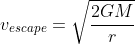
$v_{escape}=\sqrt{\frac{2GM}{r}}$

Where

v_escape gives the escape velocity of the object or body

G denotes the universal gravitational constant

M denotes the mass of the earth or relative celestial body which has a gravitational impact on the object

r denotes the length of distance between the object and centre of mass of the celestial body or earth.

The above-mentioned relation of escape velocity is used to find the escape velocities of other celestial bodies or large planets. And it is found to be the objects or celestial bodies with a larger mass will have greater escape velocity compared to the objects or celestial bodies with less mass.

Related Topics Link,

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download E-book

What is the escape velocity of earth?

We can calculate the Escape velocity of Earth by using the above-mentioned relation:

The radius of the earth is given as R= 6.410⁶m

The acceleration due to the gravity of the earth is given as g=9.8 m/s²

By, substituting the above values in the formula, we get The escape velocity of the earth as v_escape=11.2 km/s. Thus, on the earth, the value of escape velocity is found to be around 40270 kmph and in m/s, the value of escape velocity will be 11,186 m/s.

Also Read:

Why this escape velocity is required?

We know that any object to travel against the gravitational pull requires escape velocity. Now we know the escape velocity from the earth is 11 km/s. For launching the rockets like objects into space, we need to set the speed of rocket in km/hr or the object to be above the escape velocity. The other factors which affect the escape velocity are the location of the earth from where the object is launched and the earth rotation speed in kmph. This is because the escape velocity at poles is slightly different from the equator of the earth as their radius is not unique. The escape velocity of the earth is also different from the escape velocity of other celestial bodies. Lets us see some of the escape velocities of other planets and stars.

Rocket launching against the earth's gravity pull is due to velocity of rocket is set more than the escape velocity of the earth.

Celestial body	Value of escape velocity in terms of km/s
Earth	11.2
Sun	618
Moon	2.38
Jupiter	59.5
Ceres	0.64

This escape velocity concept also tells us that it is not possible to escape from a black hole, as the gravitational pull is very very high so that the escape velocity of the black hole is calculated to be more the velocity of light or space velocity (with which big objects or human cannot travel). So it is difficult to come out from a black hole.

From this article, we learnt what is escape velocity or escape speed, why this escape velocity is required, how this escape velocity is used in rocket propulsion, comparison of the escape velocities of different celestial planets and stars, the sun, moon, Jupiter, earth and so on. We also saw the concept of why it is impossible or very difficult to escape from a black hole and how this escape velocity plays an important role in the science of black holes. Now, let us see the answers to frequently asked questions about escape velocity from class 10, class 11 and class 12.
Also check-

NCERT Physics Notes:

Frequently Asked Questions (FAQs)

1. What is meant by escape velocity or what do you mean by escape velocity?

The escape velocity meaning can be given as the required velocity of the object to move against the gravitational force or pull of the Earth or other celestial bodies.

2. Why do different planets have different escape velocities?

The different planets have different escape velocities due to the different radius and varying acceleration due to the gravity of each celestial body.

3. Give the value of escape velocity of earth?

We can calculate the Escape velocity of Earth by using the above-mentioned relation: The radius of the earth is given as R= 6.410⁶m and The acceleration due to the gravity of the earth is given as g=9.8 m/s²

By, substituting the above values in the formula, we get The escape velocity on earth is 11.2 km/s. Thus, on the earth, the value of escape velocity is found to be around 40270 kmph and in m/s, the value of escape velocity will be 11,186 m/s.

4. What is the value of escape velocity of Jupiter?

5. How do rockets escape earth gravity?

6. What is the escape velocity of moon?

7. What is the equation of escape velocity?