Universal Law of Gravitation - Formula, Application, FAQs

State newton’s law of universal gravitation

When Sir Isaac Newton was sitting under a tree in 1665, an apple fell from that tree onto the earth, he proposed the concept of gravitation.
This triggered the thought in his head that all bodies are drawn to the earth's core, where he defined gravitation as the force of attraction between any two bodies separated by a distance.
This concept was crucial in the creation of stars, as well as directing the overall structure of the universe.
At the moment, this concept has a lot of applications in physics research.
The gravitational force is the weakest of all the fundamental forces of existence.

State the universal law of gravitation class 9 or what is the law of universal gravitation and give universal law of gravitation formula

Isaac Newton, an English mathematician and physicist, proposed this law in 1687 to explain the motions of planets and their moons.

Any particle of matter in the cosmos attracts another with a force that varies directly as the product of their masses and inversely as the square of their distance, according to Newton’s law of universal gravitation.

Consider two bodies A and B, each with a mass of m1 and m2, separated by r, with the force of attraction acting on them law of gravitation gives the gravitational force between as illustrated in the diagram below:

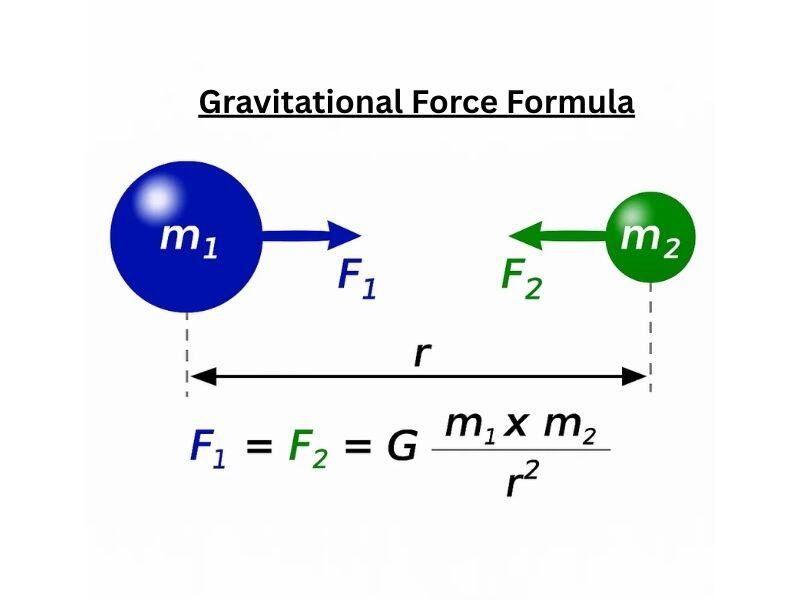
Figure 1 shows how two bodies with attraction forces F1 and F2 tend to gravitate towards the center of gravity.

The Universal gravitational Constant (G) is used here (a scalar quantity).

G has a constant value throughout the cosmos and is unaffected by the nature or size of the bodies.

Also read -

• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 12 Physics
• NCERT Solutions for All Subjects

Gravitational constant-

The gravitational constant's value is extremely difficult to calculate precisely. Henry Cavendish invented an ingenious method of determining the gravitational constant.

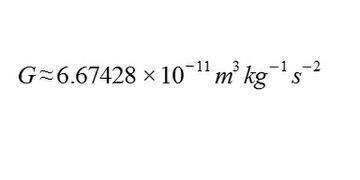
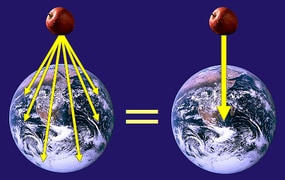
Universality of gravity-

Not only between the earth and other objects, but between all things, gravitational interactions exist with an intensity that is directly proportional to the product of their masses. Scientists use the law of universal gravitation to investigate planetary orbits. Because all objects exert gravitational impacts on each other, slight disturbances in a planet's elliptical motion can be simply explained.

Weight and gravitational force-

We saw that mass is a vital factor in Newton's law of gravity. We mistakenly believe that mass and weight are the same thing, yet they are not. The gravitational force exerted on an object of a specific mass is known as weight. The weight of an object can be calculated by multiplying its mass, m, by the acceleration due to gravity, g, at the Earth's surface. At the Earth's surface, the measured gravitational acceleration is around 9.80 m/second/second.

Weight is the measure of the gravitational force exerted on the material in a gravitational field, while mass is the measure of how much material is in an object. As a result, mass and weight are proportionate to one another, with gravity acting as the proportionality constant. As a result, it can be seen that an object's mass is constant, but its weight varies depending on its location. Consider the following scenario: if we transferred an object of mass m to the surface of Neptune, the gravitational acceleration would alter due to the difference in radius and mass between Neptune and the Earth. As a result, our object has mass m on both the Earth's surface and the surface of Neptune, but it will weigh substantially more on Neptune's surface due to the gravitational acceleration of 11.15 m/s^2.

Also Read:

• NCERT Solutions for Class 11 Physics Chapter 8 Gravitation
• NCERT Exemplar Class 11 Physics Solutions Chapter 8 Gravitation
• NCERT notes Class 11 Physics Chapter 8 Gravitation

Application of universal law of gravitation-

Newton's law of gravitation applies to both large and small objects.

When the distance between two bodies is less than 10^-9 meters, it fails.

Newton's law has a number of applications, two of which are described below:

1. This formula proven to be extremely accurate in predicting the orbits and time periods of current artificial satellites.
2. This law proved to be quite accurate in predicting solar and lunar eclipses.

What is the importance of universal law of gravitation-

1. The earth's gravitational force binds terrestrial objects to it.
2. This law explains the attractive force that exists between any two mass objects.
3. The force of attraction between the moon and the ocean water causes tides to form in the ocean.
4. With the sun, all planets make an elliptical revolution.

Also check-

• NCERT Exemplar Class 11th Physics Solutions
• NCERT Exemplar Class 12th Physics Solutions
• NCERT Exemplar Solutions for All Subjects

NCERT Physics Notes:

• NCERT Notes Class 11th Physics
• NCERT Notes Class 12th Physics
• NCERT Notes For All Subjects