Value of g - CGS, FPS, Earth, FAQs

What is Acceleration Due to Gravity (g)?

According to Newton's Second Law, a force $\mathbf{F}$ acting on a mass $\mathbf{m}$ produces acceleration a:

$
F=m a
$

If this force is due to the Earth's gravity, the acceleration produced is called acceleration due to gravity, represented by $\mathbf{g}$ :

$
F=m g
$

Thus, $g$ is the acceleration experienced by a body when it freely falls under the Earth's gravitational pull.

Is g a Constant?

Unlike $\mathbf{G}$ (universal gravitational constant), $\mathbf{g}$ is NOT constant everywhere.
The value of $g$ changes due to:

• Altitude (height above Earth)
• Depth below Earth
• Shape of Earth
• Rotation of Earth

However, a standard value is used for calculations:

$
g=9.8 \mathrm{~m} / \mathrm{s}^2
$

Why Do Objects of Different Masses Fall at the Same Rate?

The value of $g$ does not depend on the mass, size, or shape of the falling body.
This is why, as Galileo demonstrated, two objects dropped from the same height reach the ground at the same time (ignoring air resistance).
Air resistance (upthrust) is the only reason larger objects fall slower.

Direction and Unit of g

• Direction: Always toward the center of the Earth.
• SI Unit: $m / s^2$ or $N / k g$
• Dimensional Formula: $M^0 L^1 T^{-2}$

Relation Between g and G

Let us consider earth to be a sphere of mass M, radius R with the centre of earth as O. Now, if a body of mass m is placed on the surface of earth, g is the acceleration due to gravity acting on it.

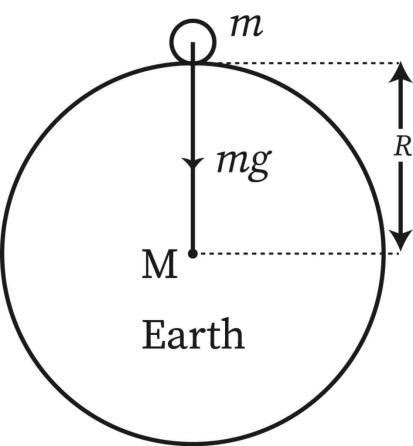
The gravitational force between Earth (mass M) and the body is:

$
F=\frac{G M m}{R^2}
$

But this force is also equal to $\mathbf{m g}$ :

$
m g=\frac{G M m}{R^2}
$

$
g=\frac{G M}{R^2}
$

g depends on Earth’s mass (M) and Earth’s radius (R) not on the body’s mass.

Mass, Radius, and Density of the Earth

Using:

$
g=\frac{G M}{R^2}
$

We can calculate Earth's mass:

$
M=\frac{g R^2}{G}
$

For radius $R=6400 \mathrm{~km}$,

$
M \approx 6.0 \times 10^{24} \mathrm{~kg}
$
Density:

$
\rho=\frac{3 M}{4 \pi R^3}
$

Variation of g-Factors Affecting Acceleration Due to Gravity

Acceleration due to gravity changes with height, depth, and Earth's shape.
Let's understand each case.
1. Variation of g With Height (Altitude)

At Earth's surface:

$
g=\frac{G M}{R^2}
$

At height $h$ above the surface:

$
g^{\prime}=\frac{G M}{(R+h)^2}
$

For small heights ( $h \ll R$ ):

$
g^{\prime}=g\left(1-\frac{2 h}{R}\right)
$
g decreases with increase in height - this is why gravity is slightly weaker on mountains.

2. Variation of g With Depth

At Earth's surface:

$
g=\frac{G M}{R^2}
$

At depth $\mathbf{d}$ :

$
g^{\prime}=g\left(1-\frac{d}{R}\right)
$

g decreases linearly with depth and becomes zero at Earth's center.

3. Variation of g Due to Earth's Shape

Earth is not a perfect sphere; it is an oblate spheroid:

• Radius at equator: larger
• Radius at poles: smaller

Since:

$
g \propto \frac{1}{R^2}
$

g is maximum at poles and minimum at the equator.

Also Read:

• NCERT Solutions for Class 11 Physics Chapter 8 Gravitation
• NCERT Exemplar Class 11 Physics Solutions Chapter 8 Gravitation
• NCERT notes Class 11 Physics Chapter 8 Gravitation

Why is g Zero at the Centre of the Earth?

At the centre, gravitational pull from all sides cancels out, resulting in:

$
g=0
$

Summary

• $\mathrm{g}=9.8 \mathrm{~m} / \mathrm{s}^2$ near Earth's surface
• g varies with height, depth, and Earth's radius
• $g$ is maximum at poles and minimum at equator
• g becomes zero at Earth's centre
• Objects fall at the same rate because $g$ is independent of mass

Also read -

• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 12 Physics
• NCERT Solutions for All Subjects

NCERT Physics Notes:

• NCERT Notes Class 11th Physics
• NCERT Notes Class 12th Physics
• NCERT Notes For All Subjects