Wave Number - Definition, Formula, Symbol, FAQs

Edited By Team Careers360 | Updated on Jul 02, 2025 05:07 PM IST

In this article, we will go through a very interesting property of electromagnetic waves, that is wave number and some of it’s related terms like what is wave number or definition of wave number, unit of wave number, wave number symbol (k symbol) or k meaning in numbers, wave number formula, wave number and frequency relation and at last, we will also see what is wavelength and wavelength symbol.

Wave Number - Definition, Formula, Symbol, FAQs

wave

So, let’s start with our very first topic that we all have already heard in class 11 …

What is wave number in physics?/Define wave number.

Wave number definition- it is the number of whole unit cycle of an electromagnetic waves. In simple language, wave number is defined as number of wavelength per radial (this means, these emw waves in an electromagnetic field are of one meter).

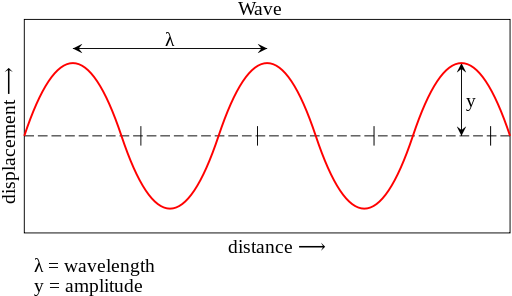
Wavelength is the distance between two consecutive crests or troughs.

As these emw waves specifically stated in vacuum state hence when we talk about the wave number it is reffered for vacuum space. Common terms wave numbers are like angular wave number or propogation number (in context with angular wavelength and propagation wave).

Also read -

What is wave number in chemistry?

In chemistry also wave number is the number of wavelength per unit distance.

Wave number symbol

Wave number is represented as k symbol in physics and nu(ṽ) symbol in chemistry notation is same. The reciprocal of wavelength is called wave no., writing mathematically we see that

k = 1 /λ or

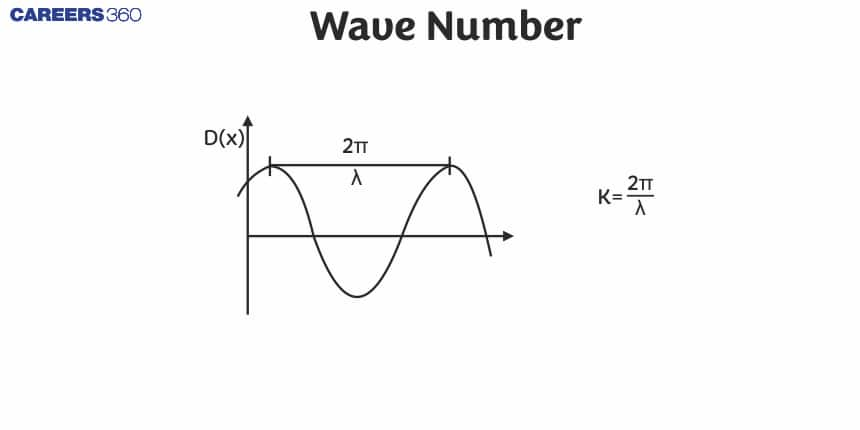
k = 2П/λ (2 pi lambda)

here lambda (λ) means wavelength.

There is relation between wavelength and wave number.

Diagram Description automatically generated

Unit of wave number

Si unit of wave number will be derived as reciprocal of wavelength. Hence, si unit of wave number is per meter (m -1).

Or can be written as radian per meter (rad/m).

Related Topics Link,

Dimensional formulae of wave number (k)

[M⁰L^-1T⁰]

Wave number formula

Now we will see how to find wave no. Formula, according to wave number equation wave number formula is

K=k_on

K_ois the absolute wave number that is wave number in vacuum.

Here n= (ɛμ)^1/2

N stands for refractive index of the given substance.

Also Read:

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Wave number equation

Though wave number is a specific term but calculation of wave number can be different for different perspective.

In physics,

We study it as wave number for matter wave.

Matter waves are known to be existing in quantum mechanics, introduced by louis de brogile. Formula for matter waves is

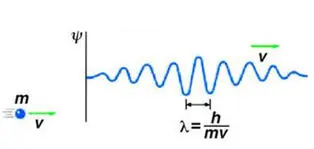
matter waves

λ = h/mv, where λ IS wavelength symbol h is Planck’s constant, m is the mass of the particle and v is the velocity of particle.

Hence, k is given as, k= 2п/ λ

In chemistry,

We study it in the field of spectroscopy.

Hence formula for wave number in spectroscopy is given as

Ṽ= 1/λ here nue bar /nu bar symbol (represented as sign of frequency symbol)

As in general,

k=ω/ v_p

here ω is 2Пν v_p is phase velocity.

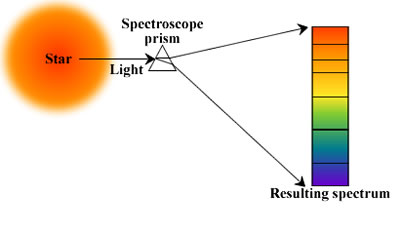
Diagram
Description automatically generated

Spectroscopy

Studying the nature of electro magnetic waves (visible light, infrared rays, x- rays, gamma rays), how are they reflected and absorbed by matter.Spectrometer is used to split the energy reflected by a matter into all types of wavelengths. To know about the properties of objects.

Spectroscopy has a vast applications in modern sciences from revealing the colour of object, to its structure, crystals lattice structures of the molecules and compounds in solid states are studied through this phenomenon that reaveals the properties of these crystals like diamond, nacl etc.

Also, it has enormous use in astronomy to find the velocity of the stars and galaxies in this expanding universe, pharmaceuticals, forensics, food and beverages. Minerology and gameology, material technology etc.

Now coming back,

In this formula of wave number there is direct relation of frequency and wave number.

And that’s how we have to calculate wave number for different perspective.

Wave number of chemistry and physics are different but performs the same function overall.

So, in total there should be no confusion between the definition of wave number.

At last, we have seen one of the property of electromagnetic wave that is wave number k along with this we have also seen relationship between wave number and wavelength, also we have calculated the frequency and wave number relation.

Also check-

NCERT Physics Notes:

Frequently Asked Questions (FAQs)

1. Define wave vector k and its significance.

Wave vector, symbol k, is a property of wave which shows the direction and magnitude of wave number or else angular wave number.

It is considered as phase lag per unit distance.

It is significant in both the fields of physics and chemistry.

We see that wave number has vast use in communication studies and also in quantum mechanics. Whereas in chemistry it plays important role for studying spectroscopy.

2. What is nu in chemistry and ν number formula. Frequency in atomic units.

Nu is the symbol of frequency used in science. Frequency is also a property of electromagnetic wave and is defined as number of complete cycles per second. Hence its SI unit is HERTZ. Dimensional formula is given as[M⁰L^-1T⁰]OR T^-1. In Sound energy, Frequency denotes the pitch of any wave/sound. That is, how much shrill or sharp the voice is.

3. Angular lambda expression. Define 1 lambda.

Wavelength is also a very important component of any electromagnetic wave. Wavelength is the distance between the two successive crests or troughs. Angular width is used in diffraction phenomenon and is known as the fringe width β denoted by the symbol beta. Its expression is given as

β= λD/d, where λ is the wavelength of source, D is the distance between two source and the screen and d is the distance between the two slits.

4. Is wave no. a scalar quantity or vector quantity?

Wave number is a scalar quantity whereas wave vector is a vector quantity representing the magnitude and direction of propagation of electromagnetic waves.

5. Define electromagnetic waves and its properties (EMW).

Waves created due to the disturbance in electromagnetic field is known as EM waves. It consists of seven different types of waves. It travels with the velocity of 3 x 10⁸ m/s in vacuum space. Its properties are wavelength, frequency, phase difference, amplitude and intensity. In today’s era there is vast use of electromagnetic waves. Studying and working in this field has in turn changed the scenario of this technology progressive generation.

6. Are higher frequency waves louder?

No, in sound waves loudness of voice is associated with the higher amplitude. Higher frequency means the pitch of the voice is high. Pitch signifies the shrillness and the sharpness of the sound.

7. What is the wave number and how is it related to wavelength?

The wave number is the number of waves that fit into one meter. It is inversely related to wavelength - as wavelength decreases, wave number increases. Mathematically, wave number (k) = 2π / λ, where λ is the wavelength.

8. Why is the wave number important in studying electromagnetic waves?

Wave number is crucial because it helps characterize the spatial frequency of a wave. It's particularly useful in spectroscopy and quantum mechanics, where it's often more convenient to work with wave numbers than wavelengths.

9. What are the units of wave number?

The standard unit for wave number is inverse meters (m⁻¹). In spectroscopy, it's often expressed in cm⁻¹, called wavenumbers.

10. How does the wave number change as you move from radio waves to gamma rays in the electromagnetic spectrum?

As you move from radio waves to gamma rays, the wavelength decreases, so the wave number increases. Radio waves have the lowest wave numbers, while gamma rays have the highest.

11. Can wave number be negative?

In most practical applications, wave number is positive. However, in some theoretical contexts, like when describing waves traveling in opposite directions, negative wave numbers can be used to indicate direction.

12. Can you explain the concept of wave number in terms of de Broglie waves?

In de Broglie's theory, particles can exhibit wave-like properties. The wave number for a particle is related to its momentum by k = p/ℏ, where p is momentum and ℏ is the reduced Planck's constant.

13. Why do scientists sometimes prefer to use wave numbers instead of wavelengths?

Wave numbers are often preferred because they're directly proportional to energy. This makes calculations and comparisons easier, especially in spectroscopy and quantum mechanics.

14. What's the difference between angular wave number and spectroscopic wave number?

Angular wave number (k) includes the 2π term and is measured in radians per meter. Spectroscopic wave number (ν) doesn't include 2π and is typically measured in cm⁻¹. The relationship is k = 2πν.

15. What's the relationship between wave number and wave vector?

The wave vector is a vector quantity whose magnitude is the wave number. In one dimension, they're essentially the same, but in 3D, the wave vector provides directional information that the scalar wave number doesn't.

16. Why is wave number important in infrared spectroscopy?

In IR spectroscopy, absorption peaks are typically reported in wave numbers (cm⁻¹). This is because wave numbers are directly proportional to energy, making it easier to interpret and compare spectra.

17. How does the wave number change when light enters a medium with a different refractive index?

The wave number changes in proportion to the refractive index. If light enters a medium with a higher refractive index, the wave number increases, as the wavelength decreases but the frequency remains constant.

18. Can you explain the concept of group velocity using wave numbers?

Group velocity is the velocity of a wave packet and is given by dω/dk, where ω is angular frequency and k is wave number. This relationship shows how the speed of a wave group depends on how frequency changes with wave number.

19. How is wave number used in describing standing waves?

For standing waves, the wave number is quantized and depends on the length of the medium. For a string fixed at both ends, the allowed wave numbers are k = nπ/L, where n is an integer and L is the string length.

20. How does the uncertainty principle relate to wave number and position?

The uncertainty principle states that the product of uncertainties in position (Δx) and wave number (Δk) must be greater than or equal to 1/2. This fundamental limit affects our ability to simultaneously measure a particle's position and momentum precisely.

21. How does wave number affect the diffraction of light?

Diffraction effects are more pronounced for larger wavelengths (smaller wave numbers). This is why radio waves (low wave number) can diffract around buildings, while visible light (higher wave number) creates sharp shadows.

22. How is wave number used in describing the Doppler effect?

The Doppler effect causes a change in the observed wave number when there's relative motion between the source and observer. The change in wave number is proportional to the relative velocity and the original wave number.

23. How does the wave number of a photon change during Compton scattering?

In Compton scattering, the wave number of the scattered photon decreases. The change in wave number depends on the scattering angle and the initial photon energy, demonstrating the particle-like nature of light.

24. How does wave number relate to the resolving power of a diffraction grating?

The resolving power of a diffraction grating is proportional to the product of the wave number and the number of lines in the grating. Higher wave numbers (shorter wavelengths) allow for better resolution.

25. How is wave number used in describing the quantum harmonic oscillator?

In the quantum harmonic oscillator, the wave number of the oscillator's motion is related to its energy levels. The allowed energies are given by E = (n + 1/2)ℏω, where ω is the angular frequency and n is an integer.

26. Can you explain how wave number is used in the WKB approximation?

The WKB approximation uses the local wave number to construct approximate solutions to linear differential equations. It's particularly useful in quantum mechanics for finding wavefunctions in slowly varying potentials.

27. Can you explain the concept of wave number mixing in nonlinear optics?

Wave number mixing in nonlinear optics refers to processes where waves with different wave numbers interact to produce new waves. Examples include sum and difference frequency generation, where the new wave number is the sum or difference of the input wave numbers.

28. How is wave number used in describing the quantum tunneling effect?

In quantum tunneling, the wave number becomes imaginary in the classically forbidden region. This leads to an exponentially decaying wavefunction, but with a non-zero probability of the particle appearing on the other side of the barrier.

29. Can you explain how wave number is related to the concept of group velocity dispersion?

Group velocity dispersion describes how the group velocity of a wave depends on its wave number. Mathematically, it's given by the second derivative of angular frequency with respect to wave number. It's crucial in understanding pulse propagation in optical fibers.

30. How does the wave number of light change during Rayleigh scattering?

In Rayleigh scattering, the wave number of the scattered light remains the same as the incident light. However, the intensity of scattering is strongly dependent on wave number, varying as the fourth power of wave number.

31. How is wave number used in describing the Aharonov-Bohm effect?

In the Aharonov-Bohm effect, the phase of an electron's wavefunction is affected by electromagnetic potentials, even in regions where the fields are zero. This phase shift can be described in terms of a change in the effective wave number of the electron.

32. How does the wave number of a photon change during the Mossbauer effect?

In the Mossbauer effect, the wave number of the emitted or absorbed photon doesn't change significantly. This is because the recoil energy is taken up by the entire crystal lattice rather than a single nucleus, allowing for extremely precise spectroscopy.

33. What's the significance of the cutoff wave number in waveguides?

The cutoff wave number in a waveguide is the minimum wave number that can propagate in the guide. Waves with lower wave numbers (longer wavelengths) are attenuated. This is important in designing waveguides for specific frequency ranges.

34. How is wave number used in describing the quantum Hall effect?

In the quantum Hall effect, the Hall conductivity is quantized in units of e²/h, where e is the electron charge and h is Planck's constant. The wave number of the electrons' cyclotron orbits is crucial in understanding this quantization.

35. Can you explain how wave number is related to the concept of Anderson localization?

Anderson localization occurs when waves in a disordered medium become localized due to interference effects. The localization length depends on the wave number and the strength of disorder. Generally, higher wave numbers (shorter wavelengths) are less susceptible to localization.

36. How is wave number related to the energy of a photon?

The energy of a photon is directly proportional to its wave number. The relationship is E = hck, where h is Planck's constant, c is the speed of light, and k is the wave number.

37. How does the wave number relate to the frequency of a wave?

Wave number (k) is related to frequency (f) by the equation k = 2πf/c, where c is the speed of light. As frequency increases, so does the wave number.

38. How is wave number used in the quantum mechanical description of a particle in a box?

In the particle in a box model, allowed wave numbers are quantized and determine the energy levels. The wave number is given by k = nπ/L, where n is an integer and L is the box length.

39. How does the concept of wave number apply to matter waves?

For matter waves, the wave number is related to the particle's momentum by k = p/ℏ. This relationship is fundamental to quantum mechanics and underlies phenomena like electron diffraction.

40. How does the wave number of light change during the photoelectric effect?

The wave number of the light doesn't change during the photoelectric effect. Instead, the energy associated with the wave number is transferred to the electrons, causing them to be ejected from the material.

41. What's the significance of the Nyquist wave number in signal processing?

The Nyquist wave number is the highest wave number that can be accurately represented in a discretely sampled signal. It's equal to π/Δx, where Δx is the sampling interval, and is crucial for avoiding aliasing.

42. What's the relationship between wave number and the refractive index of a medium?

The wave number in a medium is related to the refractive index by k = nk₀, where n is the refractive index and k₀ is the wave number in vacuum. This shows that the wave number increases in media with higher refractive indices.

43. What role does wave number play in the phenomenon of dispersion?

Dispersion occurs because the refractive index of a medium often depends on the wave number. This leads to different wave numbers traveling at different speeds, causing effects like the separation of white light into colors in a prism.

44. Can you explain how wave number is related to the concept of phase velocity?

Phase velocity (v_p) is related to angular frequency (ω) and wave number (k) by v_p = ω/k. This relationship shows how the speed of a wave's phase depends on its frequency and spatial periodicity.

45. What's the significance of the Brillouin zone in terms of wave numbers?

The Brillouin zone is a region in wave number space that completely describes the physics of waves in a periodic medium. It's crucial in solid-state physics for understanding electronic and vibrational properties of crystals.

46. Can you explain the concept of evanescent waves in terms of wave numbers?

Evanescent waves occur when the wave number in the direction of propagation becomes imaginary. This happens in total internal reflection and leads to an exponentially decaying field rather than a propagating wave.

47. What's the relationship between wave number and the de Broglie wavelength?

The wave number is inversely proportional to the de Broglie wavelength. Specifically, k = 2π/λ, where λ is the de Broglie wavelength. This relationship is crucial in quantum mechanics for describing particle-wave duality.

48. How does the concept of wave number apply to phonons in solid-state physics?

In solid-state physics, phonons (quantized lattice vibrations) are characterized by their wave number and frequency. The relationship between these (the dispersion relation) is crucial for understanding thermal and electrical properties of materials.

49. How does the wave number of light change during Raman scattering?

In Raman scattering, the change in wave number of the scattered light corresponds to the energy of vibrational or rotational transitions in the scattering molecule. This shift in wave number is called the Raman shift.

50. What's the significance of the critical wave number in the theory of instabilities?

The critical wave number in instability theory is the wave number at which a system transitions from stable to unstable behavior. It's important in fluid dynamics, plasma physics, and other fields studying pattern formation.

51. How is wave number used in describing the photoelectric effect?

In the photoelectric effect, the wave number of the incident light determines whether electrons will be ejected. There's a minimum wave number (corresponding to a maximum wavelength) below which no electrons are emitted, regardless of intensity.

52. How does the wave number of a photon relate to its momentum?

The momentum of a photon is directly proportional to its wave number. Specifically, p = ℏk, where p is momentum, ℏ is the reduced Planck's constant, and k is the wave number. This relationship is a fundamental aspect of quantum mechanics.

53. What's the significance of the plasma wave number in plasma physics?

The plasma wave number is a characteristic wave number associated with plasma oscillations. It's related to the plasma frequency and is important for understanding wave propagation and instabilities in plasmas.

54. What's the relationship between wave number and the Fermi wave vector in solid-state physics?

The Fermi wave vector is the wave number of electrons at the Fermi energy in a metal. It's a crucial concept in the free electron model and determines many properties of metals, including their electrical and thermal conductivity.

55. Can you explain the concept of wave number space (k-space) in crystallography?

Wave number space, or k-space, is the Fourier transform of real space in crystallography. It's useful for describing diffraction patterns and electronic states in crystals. Each point in k-space represents a wave with a specific wave number and direction.

56. How does the concept of wave number apply to gravitational waves?

Gravitational waves, like electromagnetic waves, can be characterized by their wave number. The wave number of gravitational waves is related to their frequency and the speed of light. Detecting gravitational waves of different wave numbers provides information about different astrophysical phenomena.