Electromagnetic Waves - Definition, Mathematical Representation, Equation, Electromagnetic Spectrum, FAQs

Edited By Team Careers360 | Updated on Nov 12, 2024 11:15 PM IST

In Physics, the abbreviation EM or EM meaning is given as Electromagnetic Waves. Electromagnetic waves are discovered by the physicist Heinrich Hertz experimentally and the basic idea of EM wave definition is taken from the Maxwell electromagnetic wave theory and as a result of Maxwell equations, Electromagnetic waves are considered to be the fundamental of the electrodynamics subject. In this article, let us see an introduction to electromagnetic waves, em theory, energy of em wave, and try to understand what are electromagnetic waves, what is the graphical representation of the em waves and by what these electromagnetic waves are produced with some electromagnetic waves examples.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

Define Electromagnetic Waves
Electromagnetic wave equation derivation:
Application of Electromagnetic waves

Electromagnetic Waves - Definition, Mathematical Representation, Equation, Electromagnetic Spectrum, FAQs

Also check-

Define Electromagnetic Waves

According to electromagnetic theory, electromagnetic waves definition is given as the waves which are formed due to the vibrations created between the Electric and Magnetic field. In short, Electromagnetic waves are composed of the oscillation electric field and magnetic field. In vacuum, the velocity of electromagnetic wave is calculated to be 3.00×10⁸m/s (which is also the velocity of light). Electromagnetic waves travel through space at a speed of light.The velocity of electromagnetic wave in medium is given by the equation v =c/n , where c is the velocity of light and n is the refractive index of the respective medium.

How are Electromagnetic Waves Produced?

When Electric fields are produced by any charged particles, some kind of force is exerted on the other nearest charged particle by the electric field. The charges which are positive in nature will accelerate along the direction of the electric field and the charges which are negative in nature will accelerate along the opposite direction of the electric wave field. At the same time, it is observed that the magnetic wave field is produced by the moving charges. The magnetic field exerts a force on other nearby moving charges and this force is always exerted perpendicular to the direction of their own velocities. (Note: only velocity should be considered here, not the speed of the particles). Thus the generation of Electromagnetic waves is due to the effect of some accelerating charged particles.

In an electromagnetic wave, the electric and magnetic fields are found to be perpendicular to the electromagnetic waves. An Electromagnetic wave can be assumed as the combined electric and magnetic field which propagates through free space with light speed. This oscillation of the charged particle has some frequency f and thus the resultant EM waves will also form with the same frequency f. Let us consider the wavelength of the Em waves is λ, then λ is given by =c/f where C denotes the velocity of light and f denotes the frequency of the EM wave. Thus the source of the Electromagnetic waves is the charged particles which are accelerated. In simple words, the production of electromagnetic waves is due to oscillating charged particles. Hope, now it is clear how electromagnetic waves are produced by oscillating charges or accelerated charged particles.

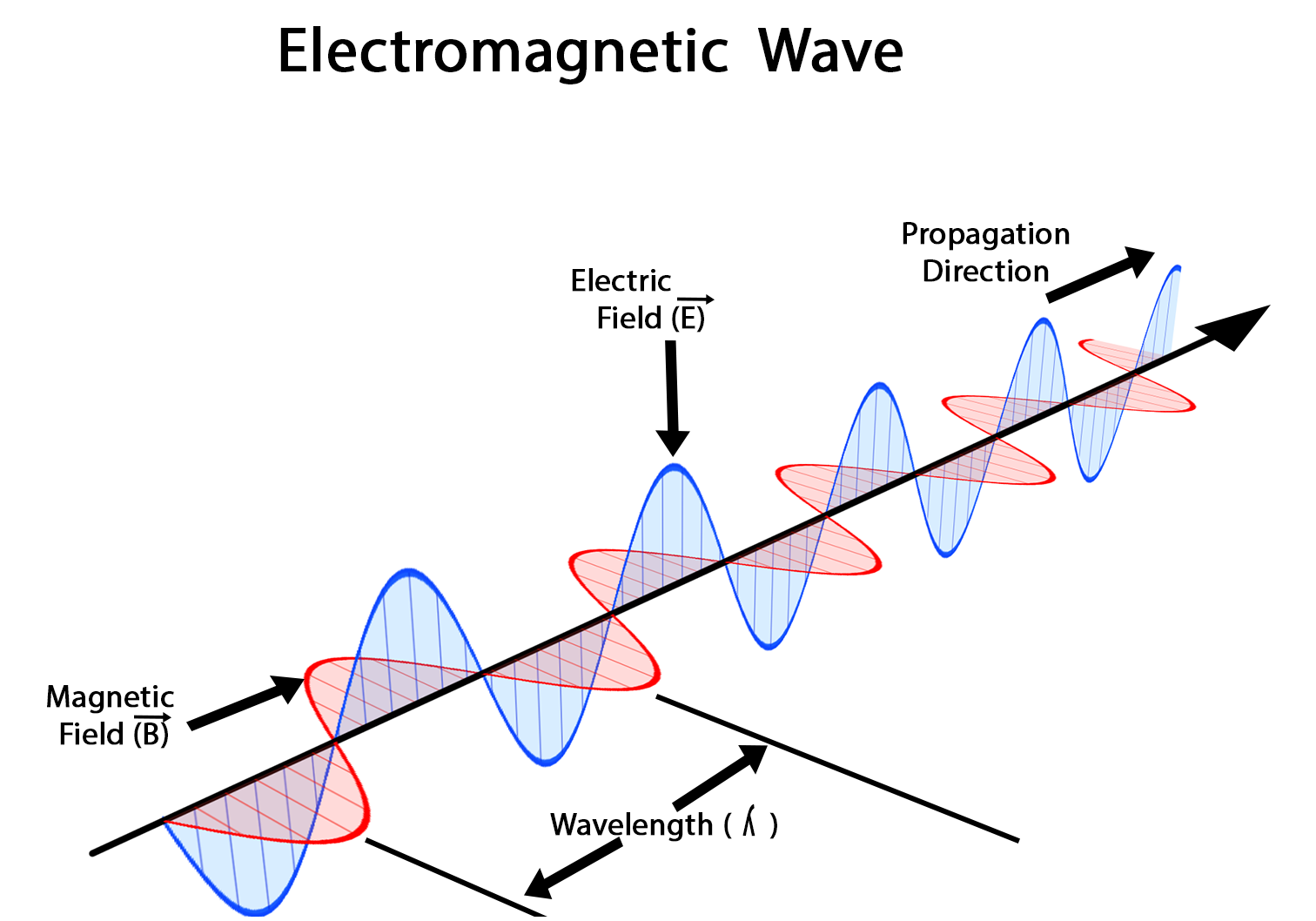
Graphical representation of the EM waves is given in the following diagram:

From the above depicted image, The electric and magnetic field of an electromagnetic wave are denoted by blue and red color waves. It is found to be that the electric and magnetic fields themselves are perpendicular to each other and also perpendicular direction of electromagnetic wave propagation. If the electric field is in x direction and magnetic field is in y direction, then the direction of propagation of electromagnetic wave is given by perpendicular direction to both x and y direction i.e in z direction. The direction of an em wave changes when the direction of electric and magnetic field changes.

Related Topics Link,

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download E-book

Mathematical Representation of EM Wave

Let us take a plane electromagnetic wave which travels in the direction of the x. Now, The electric field of an electromagnetic wave is given by E(x,t)=Emaximumcos(kx-⍵t +ɸ) and the magnetic field of an electromagnetic wave is given by B(x,t)=B_maximumcos(kx-⍵t +ɸ).

Em wave equation for respective electric and magnetic field in a plane electromagnetic wave is given by $\vec E \times \vec B$ , and the velocity of electromagnetic wave is parallel to $\vec E \times \vec B$ .

where E denotes the electric field vector and B denotes the magnetic field vector.

According to maxwell's electromagnetic wave theory of light, electromagnetic waves formula is given by

▽ . E = 0

▽ . B =0

$\Delta \times E=-\frac{\partial B}{\partial t}$

$\Delta \times E=-\frac{\partial E}{\partial t}\mu \varepsilon$

Electromagnetic wave equation derivation:

The Electromagnetic wave equation gives the propagation of Em waves in medium or vacuum. It is a second order partial differential equation and also it takes the wave equation in 3d form.

The homogeneous form of the electromagnetic rays is given by

$\frac{\partial B}{\partial x^2}\mu \varepsilon-\frac{\partial B}{\partial t^2}=0$

$\frac{\partial E}{\partial x^2}\mu \varepsilon-\frac{\partial E}{\partial t^2}=0$

Where μ = permeability in medium or free space

ε= permittivity in medium or free space

Also Read:

Intensity of em wave

Let us consider the electromagnetic waves that transport in free space Now, the intensity of electromagnetic wave I can be written as,

$I=\frac{P}{A}=\frac{1}{2}C\varepsilon_0E^2=\frac{1}{2}\frac{c}{\mu_0}\varepsilon_0 E^2$

The above equation gives the intensity of the electromagnetic wave equation in free space.

Where μ₀ = permeability in free space

ε₀ = permittivity in free space

C= velocity of light (velocity of electromagnetic wave in free space= 3 ×10⁸m/s)

Electromagnetic spectrum

In a plane, electromagnetic wave travels in free space are classified according to their individual frequency or their respective wavelengths. This wavelength differs from one light to the other. For example,

The Wavelength of Visible light will be around from 400 nm to 700 nm
The Wavelength of violet light will be around from aprox 400 nm
The Wavelength of red light will be around from aprox 700 nm

Application of Electromagnetic waves

There are plenty of applications of electromagnetic theory and em waves in practice. Let us discuss few of applications about electromagnetic waves below:

The electromagnetic signal are used to transmit energy in free space
We can also find the application of the em waves in communication.
Electromagnetic fields and waves are also used in RADAR applications.
UV rays which are considered to be em waves are used in the detection of forged documents.
IR rays are used for night cameras and security cameras.

From this article, we learnt expansion of emw waves, electromagnetic waves meaning, from what electromagnetic waves can be produced by, the value of electromagnetic velocity, the emf math reviews and application of electromagnetic waves in physics. These electromagnetic fields and waves are elaborated for class 11 and class 12. Let's discuss some FAQ’s related to em waves in class 11 and class 12.

Also read -

NCERT Physics Notes:

Frequently Asked Questions (FAQs)

1. What is em and what are em waves? OR what's an electromagnetic wave?

The EM waves can expand as Electromagnetic waves. These waves are formed due electromagnetic effects caused by oscillating charged particles. These waves are the result of an electric and magnetic wave combination.

2. What is electromagnetic theory?

The electromagnetic theory is proposed by Maxwell and this theory tells that electric flux in a closed surface is proportional to the charge enclosed by the closed surface and the magnetic flux in a closed surface is considered to be zero.

3. How to make electromagnetic waves and how an electromagnetic wave is produced?

The electromagnetic waves are produced when the charged particles oscillate. The accelerated charged particles produce the Em waves.

4. What are the electromagnetic waves formulas? (class 12 formulas)

The electromagnetic waves are produced when the charged particles oscillate. The accelerated charged particles produce the Em waves.

5. Is light an electromagnetic wave?

The answer for this question is YES. One of the best examples of em waves is light waves.The electromagnetic waves travel with the speed of light. The light waves are composed of both electric and magnetic parts.

6. Do electromagnetic waves carry energy and momentum?

Yes, the Em waves are eligible to carry energy E and Momentum p. Thus, Em waves can transfer energy through the free space.

7. What are the sources of electromagnetic waves? ( ncert class 12)

The source of em waves is accelerated charged particles. In a plane em wave, the electric field oscillates sinusoidally.