Wheatstone Bridge - Definition, Working Principle, Formula, Application, FAQs

A Wheatstone Bridge is a basic electrical circuit that measures the unknown resistances with high accuracy. It contains four resistors arranged in a rhombus and between two of its opposite corners, there is a galvanometer connected. In case the bridge is balanced, the proportion of two known resistors equals the ratio of the other two resistors which helps calculate the unknown resistance.

This Story also Contains

1. Wheatstone's Bridge
2. Application of Wheatstone bridge-
3. Limitations of Wheatstone Bridge
4. Solved Examples Based on Wheatstone's bridge
5. Summary

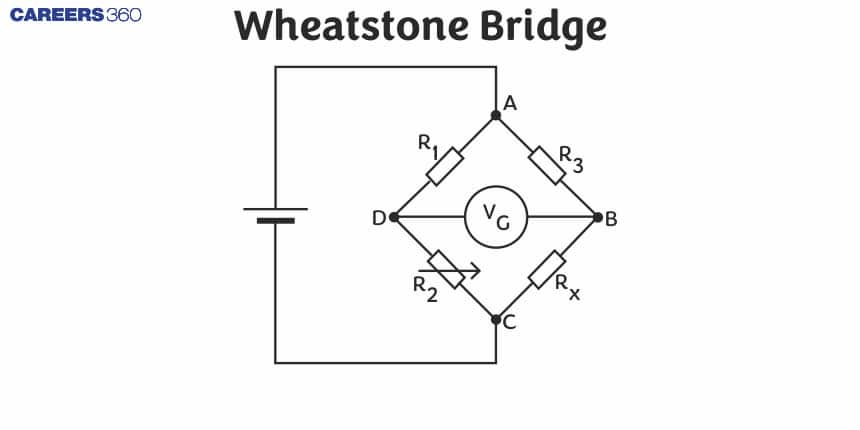
In this article, we will discuss the concept of Wheatstone's Bridge. It is important for class 12 and competitive examinations such as NEET, and JEE Main where Wheatstone Bridge not only illustrates electrical resistance principles and circuit analysis but also forms a basis for more advanced topics regarding electronics and instrumentation. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of ten questions have been asked on this concept. And for NEET two questions were asked from this concept.

Wheatstone's Bridge

It is an arrangement of four resistances which can be used to measure one of them in terms of rest. Let R is an adjustable resistance, Pand Q are known resistance and S is an unknown resistance. To obtain valur of S we will close the keys K1 and K2 and will adjust R to obtain null deflection in the galvanometer. Then the balancing condition of bridge is

PQ=RSVB=VD

(Balanced condition)
No current will flow through the galvanometer
unbalanced condition: VB>VD

(VA−VB)<(VA−VD)

Current will flow from A to B

Also read -

• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 12 Physics
• NCERT Solutions for All Subjects

Wheatstone bridge derivation

The Wheatstone bridge circuit is seen in the diagram above. R1, R2, R3, and Rx are four resistors placed in a quadrilateral ABCD pattern. Through the key K1, the points A and B are connected to a battery E.

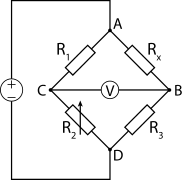
Through the key K2, the points B and D are connected to a galvanometer G.

The resistances are chosen in such a way that the galvanometer needle does not deflect and the current IG. flowing through it is zero. This is referred to as the bridge's null condition or balanced condition. R1/R2 Equals R/S in this situation.

Instead of S, an unknown resistor is attached, and the resistor R can be changed. The ratio arms are sometimes referred to as the resistors R1 and R2. The R1/R2 ratio is kept constant, and R is set to a value that meets the null condition. The unknown resistance comes from,

(R2.R1)/R3=Rx

Application of Wheatstone bridge-

1. An ideal ammeter should have zero resistance, and an ideal voltmeter should have infinite resistance, however this is impossible to achieve in practice. As a result, this circuit is unable to provide precise readings. In such instances, a Wheatstone bridge circuit can be used to get extremely exact measurements. The Wheatstone bridge circuit has been adapted in two ways for experimental purposes:

• Box at the post office
• Bridge with meter

2. Some materials (such as semiconductors) have temperature-dependent resistance. When compared to typical resistors, the variances are rather considerable. Thermistors are what they're called. The Wheatstone bridge system wheatstone bridge uses thermistors to detect small temperature changes.
3. The unknown resistor in a Wheatstone bridge circuit can be replaced with a photoresistor to measure changes in light intensity. A photoresistor's resistance is proportional to the amount of light it receives.
4. Strain and pressure can also be measured using the Wheatstone bridge.

Also Read:

• NCERT solutions for Class 12 Physics Chapter 3 Current Electricity
• NCERT Exemplar Class 12 Physics Solutions Chapter 3 Current Electricity
• NCERT notes Class 12 Physics Chapter 3 Current Electricity

Limitations of Wheatstone Bridge

1. The Wheatstone Bridge is a delicate device. In an off-balance situation, measurements may not be precise.
2. Wheatstone bridges are commonly used to measure resistances of a few ohms to a few kilo-ohms.
3. If the four resistances are not equivalent, the circuit's sensitivity is reduced.

Some important points-

• Samuel Hunter Christie devised the Wheatstone bridge circuit, which was later refined by Charles Wheatstone.
• In AC circuits, many variations of the Wheatstone bridge can be used to measure impedance, inductance, and capacitance.
• Maxwell improved the Maxwell bridge circuit, which is used in AC circuits.

Recommended Topic Video

Solved Examples Based on Wheatstone's bridge

Example 1: In a Wheatstone’s bridge, three resistances P, Q and R, are connected in the three arms and the fourth arm is formed by two resistances S₁ and S₂ connected in parallel. The condition for the bridge to be balanced will be

1) PQ=RS1+S2

2) PQ=2RS1+S2

3) PQ=R(S1+S2)S1S2

4) PQ=R(S1+S2)2S1S2

Solution

Wheat stone Bridge

It is an arrangement of four resistances which can be used to measure one of them in terms of rest

wherein

We know that PQ=RS

$$

\begin{aligned}

& \because S=\frac{S_1 S_2}{S_1+S_2} \

& \therefore \frac{P}{Q}=\frac{R\left(S_1+S_2\right)}{S_1 S_2}

\end{aligned}

$$

Example 2: The current I drew from the 5-volt source will be :

1) 0.17 A

2) 0.33 A

3) 0.5 A

4) 0.67 A

Solution:

Wheat stone Bridge

It is an arrangement of four resistances which can be used to measure one of them in terms of rest

wherein

We know that PQ=RS

The equivalent circuit is a balanced Wheatstone's bridge. Hence no current flows through arm BD here PQ=RS⇒510=1020

AB and BC are in a series

$$

\therefore R_{A B C}=5+10=15 \Omega

$$

AD and AC are in series

$$

\therefore R_{A D C}=10+20=30 \Omega

$$

ABC and ADC are in paralle

$$

\begin{aligned}

& \therefore R_{e q}=\frac{\left(R_{A B C}\right)\left(R_{A D C}\right)}{\left(R_{A B C}+R_{A D C}\right)} \

& \text { or } \quad R_{e q}=\frac{15 \times 30}{15+30}=\frac{15 \times 30}{45}=10 \Omega \

& \therefore \text { Current } I=\frac{E}{R_{e q}}=\frac{5}{10}=0.5 \mathrm{~A}

\end{aligned}

$$

Example 3: In a metre bridge experiment, the null point is obtained at 20 cm from one end of the wire when resistance X is balanced against another resistance Y . If X<Y, then where will be the new position (in cm) of the null point from the same end, if one decides to balance a resistance of 4X against Y?

1) 50

2) 80

3) 40

4) 70

Solution:

Wheat stone Bridge

It is an arrangement of four resistances which can be used to measure one of them in terms of rest

wherein

$$

\frac{R_1}{R_1}=\frac{l_1}{l_2}=\frac{l_1}{\left(100-l_1\right)}

$$

In the first case, xy=20100−20=2080=14

In the second case, 4xy=l100−l=44=l100−l

$$

l=50 \mathrm{~cm}

$$

Example 4: Four resistances of 15Ω,12Ω,4Ω and 10Ω respectively in cyclic order to form Wheatstone's network. The resistance that is to be connected in parallel with the resistance of 10Ω to balance the network is Ω⋅

1) 10

2) 5

3) 15

4) 20

Solution:

For a balanced Wheatstone bridge R1R2=R3R4 or R1R3=R2R4 R2=12Ω and R4=4Ω

As R2R4=124=3

So using R1=15Ω

We get R3=RAD=5Ω

let us connect x-ohms in parallel to the 10 -ohm resistance

i.e R3=5Ω=x∗10x+10

we get x=10Ω

So the answer will be 10.

Example 5: The Wheatstone bridge shown in the figure here gets balanced when the carbon resistor used as R₁ has the colour code (Orange, Red, Brown) The resistors R₂ and R₄ are 80$\Omega$ and 40$\Omega$, respectively. Assuming that the colour code for the carbon resistors gives their accurate values, the colour code for the carbon resistor, used as R₃ , would be :

1) Brown, Blue, Brown

2) Brown, Blue, Black

3) Red, Green, Brown

4) Grey, Black, Brown

Solution:

For a balanced Wheatstone network,

$$

\begin{aligned}

& \frac{R_1}{R_3}=\frac{R_2}{R_4} \

& \frac{R_1}{R_3}=\frac{80}{40}=2 \

& \therefore R_1=2 R_3

\end{aligned}

$$

For R1 which has the colour code (Orange, Red, and Brown)

$$

\begin{aligned}

& R_1=32 \times 10=320 \

& \therefore R_3=160

\end{aligned}

$$

where 1 - brown

6 - blue

0 -black

Summary

Wheatstone bridge method for measuring an unknown resistance has the following merits over the other methods for measuring the resistance. It has a null method therefore, the measurement of resistance made by this method is not affected by the internal resistance of the battery used. As the measurement of current or potential difference is involved, the measurements are not affected because of the fact that the ammeters and voltmeters are not ideal ones.

Also check-

• NCERT Exemplar Class 11th Physics Solutions
• NCERT Exemplar Class 12th Physics Solutions
• NCERT Exemplar Solutions for All Subjects

NCERT Physics Notes:

• NCERT Notes Class 11th Physics
• NCERT Notes Class 12th Physics
• NCERT Notes For All Subjects