Spatial Ability: Meaning, Block Counting, Question and Answer

What is Block Counting

Block counting is figuring out how many distinct blocks—whether basic or complex—are present in a particular arrangement. A simple question in this section could be something like this.

Q1: Considering the given cubes of the same size and dimensions(two different views of the same arrangement), count the number of cubes in the given arrangement without any repetition.

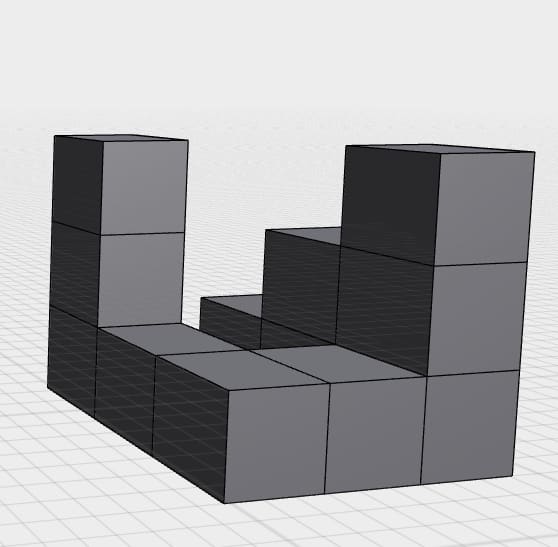
Options:

1. A= 9

2. B= 10

3. C= 11

4. D=12

Correct Answer: Option B = 10

Explanation:

Let’s go through the count based on the provided perspectives.

This comprises layers of stacked cubes.

• The front and top views give us useful pieces of information that suggest level cubes, possibly organized in blocks that the observer has an interval vision of.

• Each cube must be counted only once and in this case, no cube is obscured from either view so the sum of cubes amounts to 10.

• This approach captures each layer cube without committing the mistake of counting the same cube more than once.

Thus, the total number of cubes present in the arrangement is crucial to the solution approach, resulting in 10 cubes.

You can refer to the below articles:

• Fundamental Geometry Concepts for 2D Shapes
• Color Theory, Color Wheel for Designers
• Spatial Ability - Block Counting
• Mirror and Water Images for Design Entrances Exams
• Surface Counting: Advanced Level Techniques and Strategies

Techniques and Challenges for Block Counting

Layer-to-Layer Method

• Step 01: Break down Complex structures into individual layers.

• Step 02: Counting the blocks in each layer separately to later sum them all.

• Step 03: Identify if there are any hidden blocks or no blocks in the given space.

Symmetry vs Asymmetrical Arrangement of Blocks

The block arrangement provided usually follows a Symmetrical and Asymmetrical arrangement.

1. Symmetrical Arrangement

In block counting, symmetry describes a proportionate and balanced arrangement of blocks. One side of a symmetrical building is the mirror image of the other, and the other half is identical. Because you only need to count the blocks in half and then double the count to get the total number of blocks, this attribute makes the counting fast.

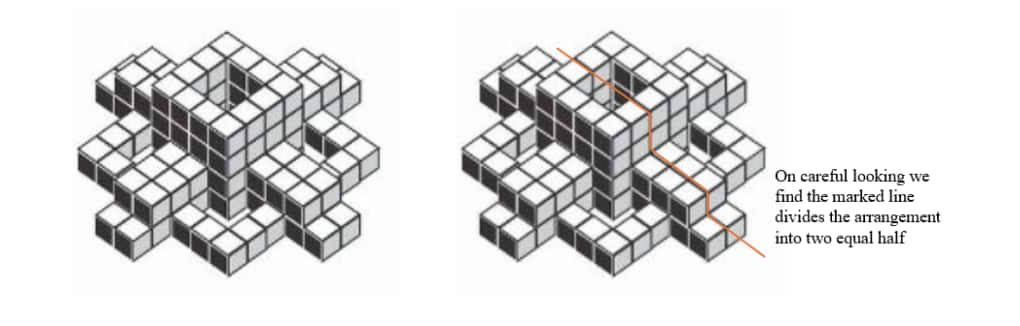
Next, we can count the number of cubes in either direction, either left or right of the arrangement, and multiply by two(2) to calculate the total number of cubes quickly.

2. Asymmetric Block Counting

Conversely, an imbalance or lack of proportion in the block arrangement is called asymmetry. Counting becomes more difficult since the two halves of an asymmetrical building are not identical. Each structure component must be looked at separately to determine the number of blocks in the given arrangement.

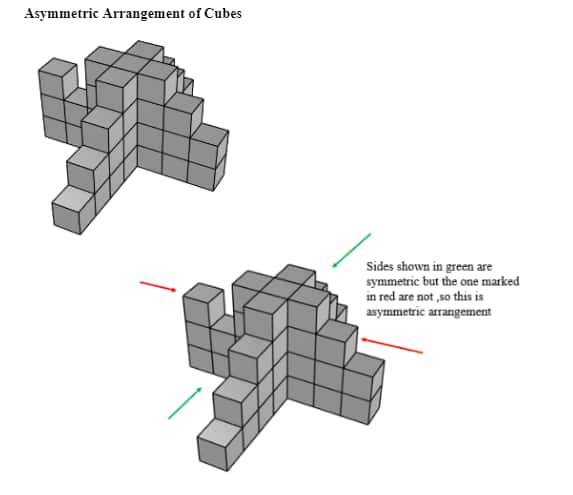
Tips & Tricks Worth Remembering

• Most aspirants were found attempting the question confidently, later to realise that they had overlooked the hidden blocks in the question image upon rechecking.

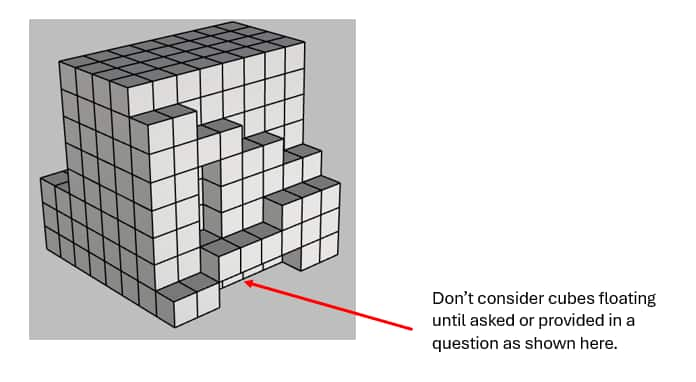
• Due to the Perspective View of the image, Miscounting is also a standard error that needs training and practice to overcome and crack the NID-DAT Examination.

• Whenever there is a cube in the air, it is evident that there is support below; thus, always consider the support below that cube as another or a set of cubes per the 3D visual image shared.

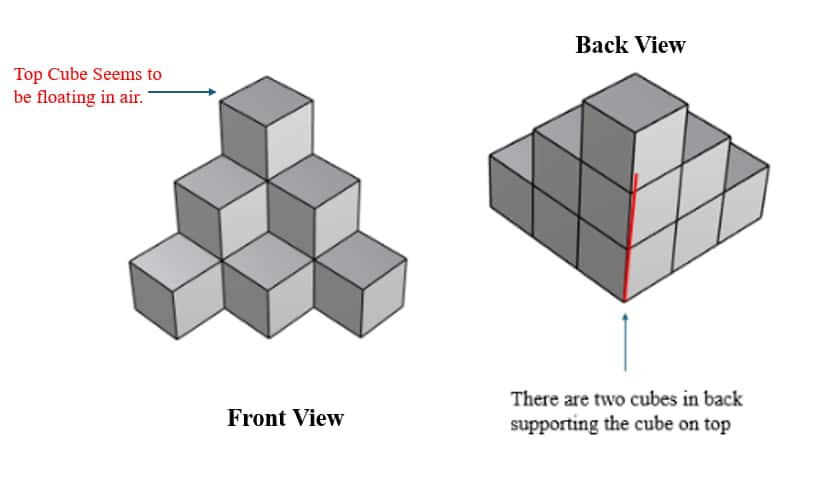
• For complex cubes, divide the arrangement into two or more fragments for easy visualisation and counting.

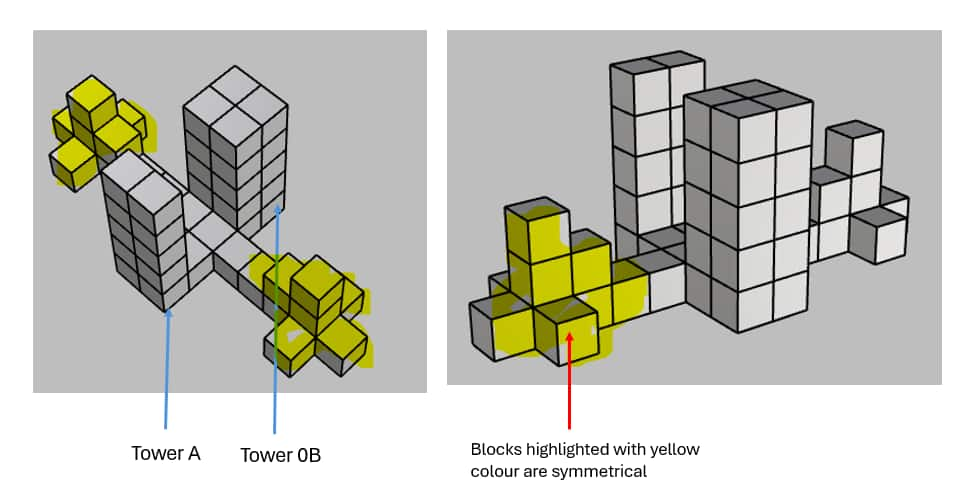
For example, in the above example, to count the cubes of the arrangement, first check if there is any asymmetry possible. Later, the arrangement is divided into Tower-A & Tower-B, including the non-common cubes between the towers.

Common Mistakes in Block Counting

Block counting is a skill that requires a keen eye for detail and spatial visualization. Even experienced aspirants can make mistakes in this area. Below are some common errors and how to avoid them:

Overlooking Hidden Cubes

One of the most frequent mistakes in block counting is overlooking hidden cubes. These cubes may not be visible in one view but can be inferred from the other view. For example, in stacked arrangements, if you see a cube floating in the air from the top view, there are likely supporting cubes underneath that are hidden from view. Similarly, cubes behind or below other cubes are often missed, leading to an incomplete count.

To avoid this, always consider cubes that may be partially or completely hidden from one perspective. Visualize the arrangement in three dimensions, taking into account the possibility of cubes being obscured by others. A quick mental check of the structure’s layering will help in identifying these hidden cubes.

Miscounting Duplicate Cubes

Another common mistake is miscounting duplicate cubes. This usually happens when cubes appear multiple times from different perspectives. For example, a cube might be visible from the front in a partially visible form and then appear fully visible from the top. If not careful, it may be counted twice, once from each view.

To prevent this, keep in mind that overlapping cubes seen in different angles are the same. Make sure you are only counting each cube once by tracking which cubes you have already counted from each perspective. Mentally consolidate the views to avoid duplication.

Confusing Symmetry and Asymmetry

When dealing with symmetrical arrangements, it's easy to assume that the structure is the same on both sides, which may lead to errors in counting. In symmetrical block arrangements, you can count one side and simply double the result. However, asymmetrical arrangements do not follow this rule and require a more careful, individual assessment of each layer and section.

For asymmetrical structures, focus on counting the blocks in each section independently and avoid relying on symmetry. Be cautious not to assume that the number of blocks in one half is the same as the other unless symmetry is explicitly clear. Always approach each side as a separate unit for an accurate count.

Spatial Ability questions:

Q1: For the given two views of the same arrangement of cubes, count the number of cubes.

Hint: Try to find a line that divides the arrangement and break it down into two parts for counting

Correct Option: 12 cubes

Explanation:

• The two views show different perspectives of the same arrangement.
  
  

• You can divide the arrangement into two parts, each containing 6 cubes.
  
  

• By counting the cubes in both parts and adding them together, you get a total of 12 cubes.

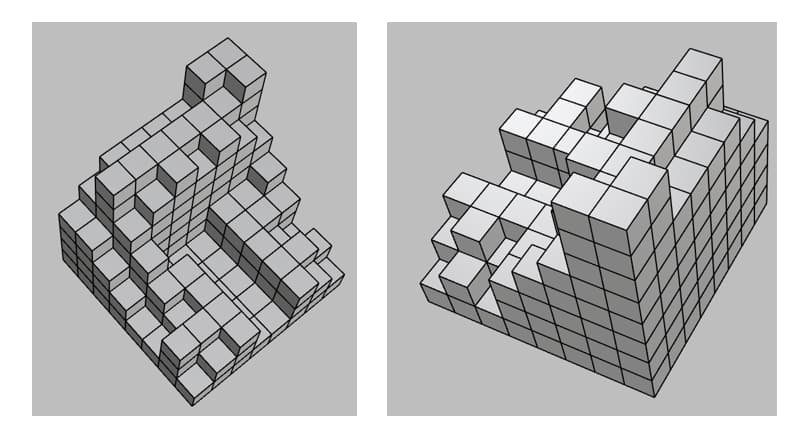
Q2: For the given arrangement of cubes, count the number of cubes.

Correct Option: 20 cubes

Explanation:

• The arrangement is a 3D stack of cubes in a circular shape.
  
  

• When analyzing the stack from the given view, we see a cylindrical shape formed by multiple cubes.

The total number of cubes in this arrangement, when counted from the visible faces, is 20.