Surface Counting: Advanced Level Techniques and Strategies

In this article, we share the approach for counting the number of shapes in the given parent volume that consists of multiple sub-shapes/volumes, e.g. A stack of cubes is given, and some cubes are missing. The focus is also on introducing the concept of platonic solids and their understanding from DAT examinations and Surface counting advanced level questions.

This Story also Contains

1. Introduction to Regular Polyhedron (Platonic Solids)
2. Introduction to Symmetry and Asymmetry in the Compositions for Surface Counting.
3. Visualizing the Symmetry/Asymmetry in Surface Counting
4. Step-by-Step Methodology for Counting Surfaces
5. Surface Counting Advanced Level with Answers
6. Surface counting advanced level with answers:

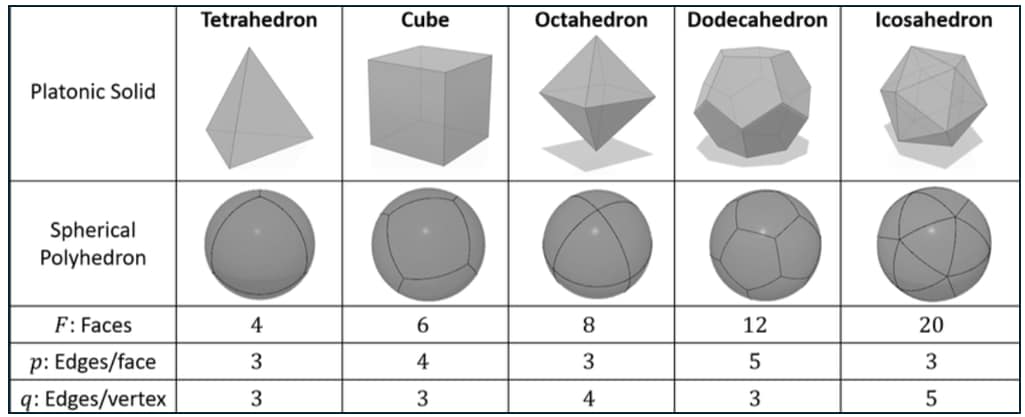
Introduction to Regular Polyhedron (Platonic Solids)

Platonic solids are a unique class of highly symmetric three-dimensional objects with equal faces, edges, and angles. The Greek philosopher Plato gave these solids their namesake and connected them to the elements of classical philosophy.

These volumes/solids are considered Platonic for the following properties.

1. Equilateral Faces: The dimensions and forms of every face are the same.

2. Equal Angles: Every internal angle is equal.

3. Vertices: An equal number of faces are joined by each vertex.

4. Every solid possesses a great degree of symmetry.

There are 05 types of fundamental Platonic Solids.

• Tetrahedron: 04 faces in a triangle
• Hexahedron or cube: 06 square faces
• Octahedron: 08 equal faces
• Dodecahedron: 12 faces in a pentagon
• Icosahedron: 20 triangular faces

Introduction to Symmetry and Asymmetry in the Compositions for Surface Counting.

The different types of symmetrical and asymmetrical shapes are as follows.

1. Symmetrical Shapes

• Symmetry refers to the shape's ability to be split into mirror-image segments or to remain unchanged when rotated around an axis. Because of their homogeneous and predictable characteristics, symmetric volumes are simpler to visualise and analyse.
• For example, as mentioned earlier, the tetrahedron, cube, octahedron, dodecahedron, and icosahedron are platonic solids. These shapes have equal faces, edges, and angles and are highly symmetrical. Understanding symmetry also builds on concepts like lines of symmetry, rotational symmetry, and reflection, which are introduced in Fundamental Geometry Concepts for 2D Shapes and then extended to 3D forms.

2. Asymmetric Shapes

Asymmetrical shapes are three-dimensional shapes that lack translational symmetry points, axes of rotation, and planes of reflection. Because of their irregular and unpredictable characteristics, asymmetric shapes are more challenging to understand and depict.

For example, organic volumes/shapes like rocks and trees are unlike most naturally occurring structures.

You can refer to the below articles:

• Color Theory, Color Wheel for Designers
• Spatial Ability - Block Counting

Visualizing the Symmetry/Asymmetry in Surface Counting

Two views(Perspective and Right Side view ) of the same object are given. Count the Number of Surfaces for the given shape.

Solution: By marking a line from the middle, the shape provided can be divided from the centre, and thus it is symmetrical. This reduces the effort for counting the surfaces one by one instead of counting the surface from the centre and multiplying by two to count the total possible surfaces in such given volumes quickly.

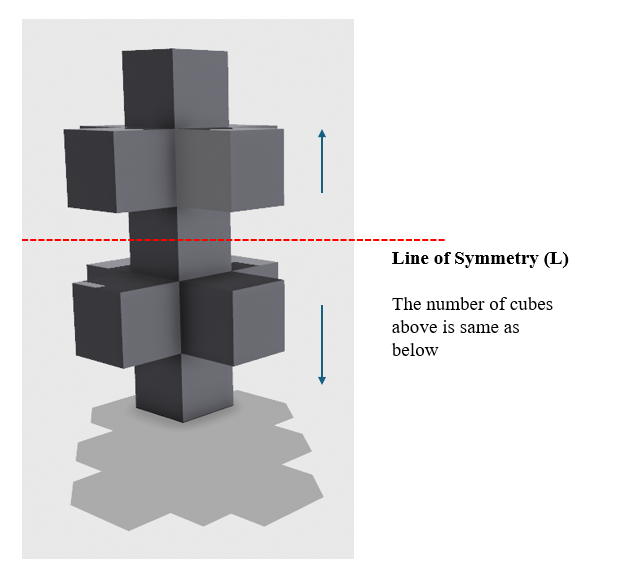
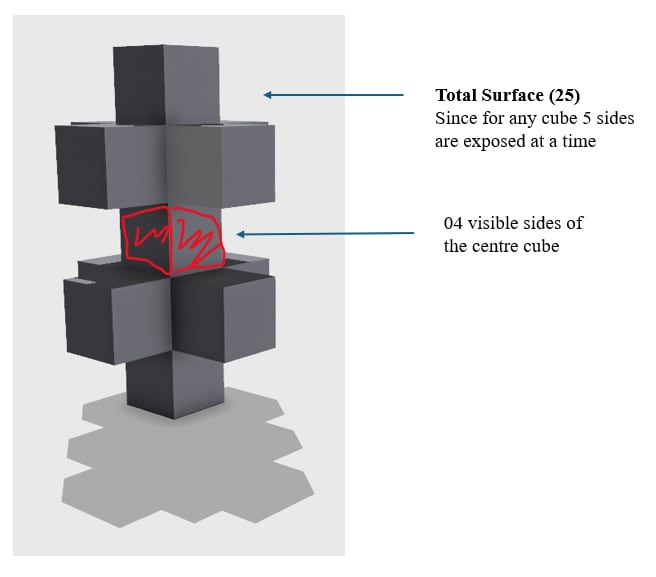
Total Exposed Surfaces = 25 X 2 (for both top and bottom) + 4 sides for centre cube

= 50+4

= 54 sides

Step-by-Step Methodology for Counting Surfaces

Step-by-Step Procedure for Counting Surfaces

1. Pinpoint symmetry first

Symmetry makes counting easier since it enables you to count only one part and multiply. Start by determining whether the shape can be split into reflected or duplicated parts. If the shape is symmetrical across an axis, you can count the surfaces on just one side and then double it. This is a labor-saving approach that minimizes mistakes.

2. Break down into simple units

Complex solids tend to look confusing initially. Divide them mentally into simple shapes such as cubes, prisms, or pyramids. Once separated, count surfaces on each individual unit independently and then add the counts, ensuring to account for any common or internal surfaces. Step-by-step division helps cope even with very complex forms.

3. Count visible surfaces direction-wise

Rather than attempting to visualize the entire shape in a single glance, examine it from direction to direction. Begin with the top view and tally all surfaces that are visible from above. Then, proceed to front, sides, back, and bottom views sequentially. This systematic process makes sure that no surfaces are omitted and avoids duplication.

4. Include or exclude surfaces from cuts or additions

When shapes have been altered — that is, when something is added or removed — the overall surface number changes. With additions, new surfaces come into being, and common faces between merged shapes may be lost. With subtracting or cutting out pieces, new inner surfaces become visible. Always modify your end surface number by accurately keeping track of these alterations to get an exact figure.

Surface Counting Advanced Level with Answers

Given below are practice questions for students to refer to:

Practise Question 01: Below are two views of the same object. Count the number of surfaces in the given shape.

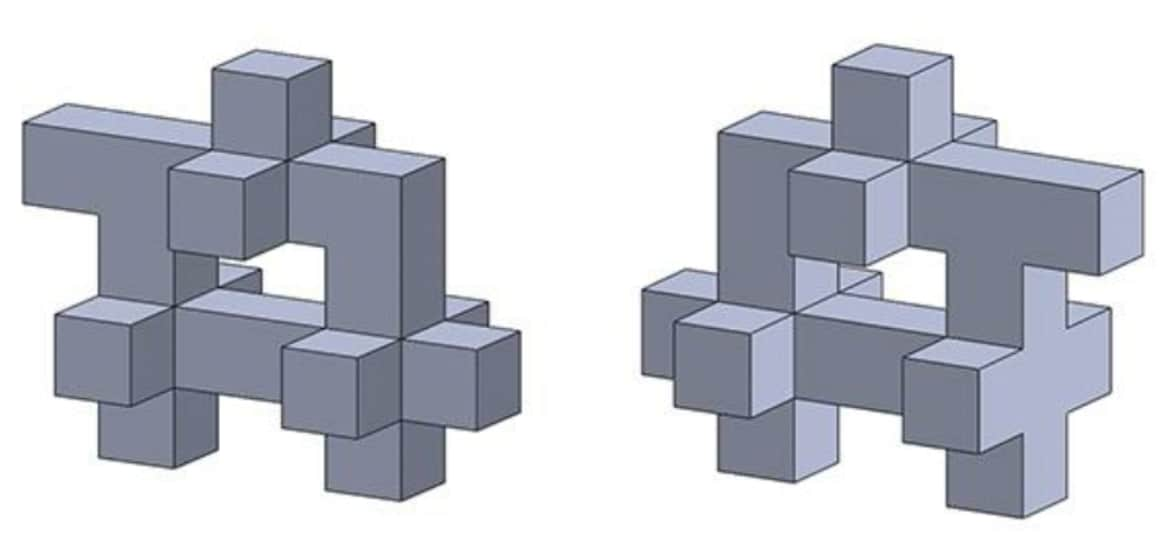
Hint: Primarily check if a symmetry/asymmetry in shape is possible across any axis.

Count all faces in one direction at a time, like counting all the faces visible from the top.

Practise Question 02: Two perspectives of the same solid, as shown below. Count the number of surfaces in the object, and consider the hidden faces flat.

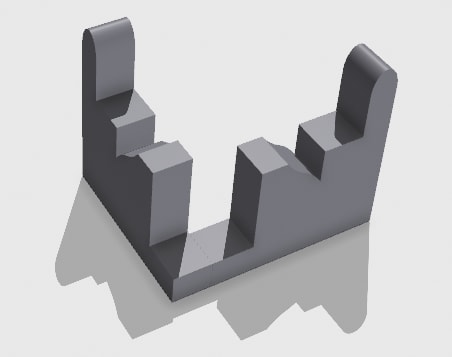
D. The surface formed by the Intersection of solids

In specific questions, a solid is given, and a part is cut out of the solid, thus exposing the new cut-out surfaces of the solid. The candidate must count the new surfaces exposed/formed by this subtraction operation. The addition operation is also done to make new surfaces in some instances.

Let us understand with the help of an example.

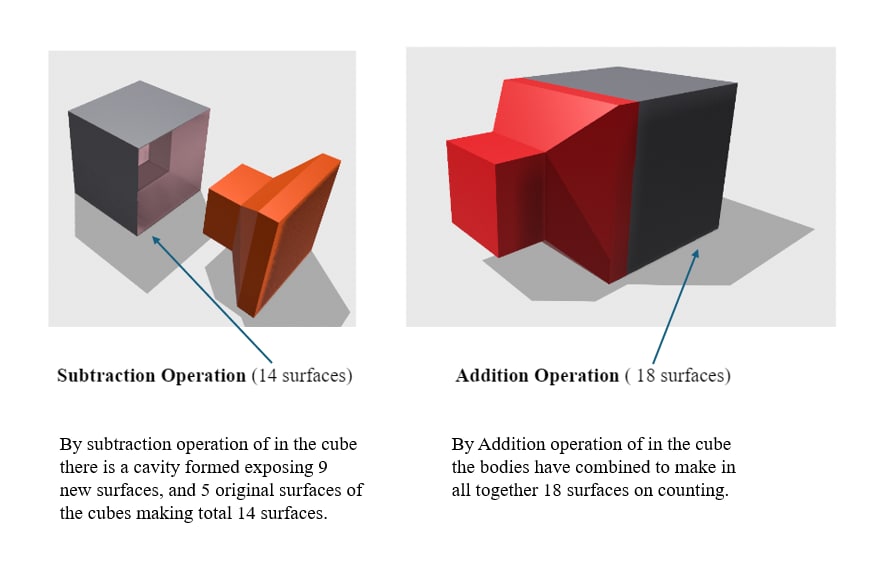
You can also refer to:

• Mirror and Water Images for Design Entrances Exams
• Surface Counting: Advanced Level Techniques and Strategies

Surface counting advanced level with answers:

Ques 01 : From one side of a solid cube of each side 2 units, a square pyramid of height 1 unit was removed, as shown in the image, resulting in a solid(in grey colour) with 9 surfaces. If one more pyramid of the same dimensions is removed from another side of the resultant solid, how many surfaces can the new resultant solid have?

Option A :10 Sides

Option B :11 Sides

Option C :12 Sides

Option D :13 Sides