Balancing Chemical Equations - Definition, Method, Formulas, Examples, FAQs

Q: What is the balanced form of the calcium hydroxide-nitric acid reaction : Ca(OH)2 + HNO3 → Ca(NO3)2 + H2O ?

Ca(OH) 2 + 2HNO 3 → Ca(NO 3 ) 2 + 2H 2 O is the balanced chemical equation of the calcium hydroxide-nitric acid reaction.

Q: Write the balanced equation for C3H8 + O2 → CO2 + H2O

C 3 H 8 + 5O 2 → 3CO 2 + 4H 2 O

Balancing Chemical Equations - Definition, Method, Formulas, Examples, FAQs

Edited By Team Careers360 | Updated on Jul 02, 2025 04:26 PM IST

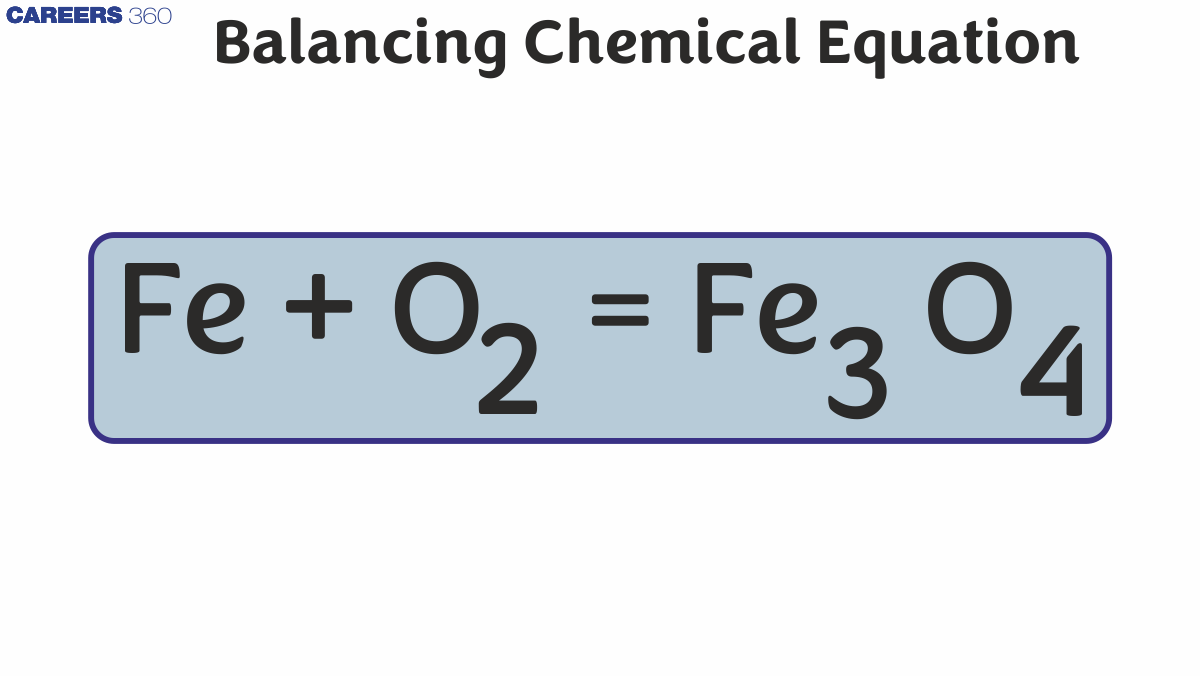
When the reactant and product sides of an equation have the same number of each element, the equation is balanced. To accurately depict the rule of conservation of mass, equations must be balanced. The inclusion of Stoichiometric coefficients to the reactants and products is required to balance chemical equations. This is crucial because a chemical equation must follow the laws of conservation of mass and constant proportions,

This Story also Contains

Chemical Equation:
Stoichiometric Coefficient
Balancing of chemical equation Method:

Balancing Chemical Equations - Definition, Method, Formulas, Examples, FAQs

Chemical Equation:

A chemical equation is a symbol for a chemical reaction in which the reactants and products are represented by their chemical formulae.

2H₂ + O₂ →2H₂O is an example of a chemical equation that depicts the reaction between Hydrogen and oxygen to generate water.

The part of the chemical equation to the left of the ‘→' sign is the reactant side, while the part to the right of the arrow symbol is the product side.

Stoichiometric Coefficient

The total number of molecules of a chemical species that participate in a chemical reaction is described by a stoichiometric coefficient.

It calculates the ratio between the responding species and the reaction products.

The stoichiometric coefficients of O₂ and H₂O in the reaction CH₄ + 2O₂ → CO₂ + 2H₂O are 2 and 1, respectively, in the equation CH₄ + 2O₂ → CO₂ + 2H₂O.

Stoichiometric coefficients are assigned in a way that balances the total number of atoms of an element on the reactant and product sides when balancing chemical equations.

Related Topics

Balancing of chemical equation Method:

When it comes to balancing chemical equations, the first step is to acquire the entire imbalanced equation. The combustion process between propane and oxygen is used as an example to demonstrate this method.

Step 1: Create an unbalanced equation using the chemical formulae of the reactants and products (if it is not already provided).

The molecular formula for propane is C₃H₈. It creates carbon dioxide (CO₂) and water when it comes into touch with oxygen (O₂) (H₂O).

C₃H₈ + O₂ → CO₂ + H₂O

Step 2: On the reactant and product sides, compare the total number of atoms of each element. In this situation, the number of atoms on each side can be tabulated as follows.

Chemical equation: C₃H₈ + O₂ → CO₂ + H₂O
Reactant side	Product side
3 C from C₃H₈	1 C from CO₂
8 H From C₃H₈	2 H from H₂O
2 O from O₂	3 O, 2 from CO₂ and 1 from H₂O

Step 3: On the reactant and product sides, stoichiometric factors are now applied to compounds containing an element with a specific number of atoms.

The coefficient must balance the number of atoms on each side.

The hydrogen and oxygen atoms' stoichiometric coefficients are normally assigned last.

It's time to adjust the number of atoms in the reactant and product elements.

It's important to note that the total number of atoms of an element in one molecule of a species is calculated by multiplying the stoichiometric coefficient by the total number of atoms of that element in that molecule.

When the CO₂ molecule is assigned the coefficient 3, the total number of oxygen atoms in CO₂ becomes 6. The coefficient is first assigned to c in this case.

Chemical equation: C₃H₈ + O₂ → 3CO₂ + H₂O
Reactant side	Product side
3 Carbon atoms from C₃H₈	3 Carbon atoms from CO₂
8 Hydrogen atoms from C₃H₈	2 Hydrogen atoms from H₂O
2 Oxygen atoms from O₂	7 Oxygen atoms, 6 from CO₂ and 1 from H₂O

Step 4: Step 3 is repeated until the reactant and product sides of the reactive elements have the same number of atoms. In this scenario, hydrogen is balanced next. The chemical equation is altered in this manner.

Chemical equation: C₃H₈ + O₂ → 3CO₂ + 4H₂O
Reactant side	Product side
3 C from C₃H₈	3 C from CO₂
8 H from C₃H₈	8 H from H₂O
2 O from O₂	10 O, 6 from CO₂ and 4 from H₂O

Now that the hydrogen atoms are balanced, the next element to be balanced is oxygen. There are 10 oxygen atoms on the product side, implying that the reactant side must also contain 10 oxygen atoms.

Each O₂ molecule contains 2 oxygen atoms. Therefore, the stoichiometric coefficient that must be assigned to the O₂ molecule is 5. The updated chemical equation is tabulated below.

Chemical equation: C₃H₈ + 5O₂ → 3CO₂+ 4H₂O
Reactant side	Product side
3 Carbon atoms from C₃H₈	3 Carbon atom from CO₂
8 Hydrogen atoms from C₃H₈	8 Hydrogen atoms from H₂O
10 Oxygen atoms from O₂	10 Oxygen atoms, 6 from CO₂ and 4 from H₂O

Step 5: After all of the individual elements have been balanced, the total number of atoms in each element on the reactant and product sides is compared once more.

The chemical equation is said to be balanced if there are no inequalities.

Every element now has the same number of atoms on the reactant and product sides in this example.

As a result, C₃H₈ + 5O₂ → 3CO₂ + 4H₂O is the balanced chemical equation.

EXAMPLE:

Al + O₂→ Al₂O₃ is an unbalanced chemical equation.

Traditional method

The reaction can be balanced using the old method as follows:

Chemical equation: Al + O₂ → Al₂O₃
Reactant side	Product side
1 Aluminium atom	2 Aluminum atom
2 oxygen atom	3 oxygen atom

The aluminium atoms are balanced first.

2Al + O₂ → Al₂O₃

There are two oxygen atoms on the reactant side and three on the product side, so the oxygen atoms must be balanced now. As a result, there must be three O₂ molecules that produce two Al₂O₃atoms.

2Al + 3O₂ → 2Al₂O₃ is the chemical converted equation.

Because the number of aluminium atoms on the product side has doubled, the number on the reactant side must have doubled as well

Chemical equation: 4Al + 3O₂ → 2Al₂O₃
Reactant side	Product side
4 Aluminium atom	4 Aluminum atom
6 oxygen atom	6 oxygen atom

Balanced chemical equation is found to be 4Al + 3O₂ → 2Al₂O₃

Also check-

NCERT Exemplar Class 11th Chemistry Solutions	NCERT Solutions for Class 11 Chemistry
NCERT Exemplar Class 12th Chemistry Solutions	NCERT Solutions for Class 12 Chemistry
NCERT Exemplar Solutions for All Subjects	NCERT Solutions for All Subjects

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download EBook

Frequently Asked Questions (FAQs)

1. What is the balanced form of the calcium hydroxide-nitric acid reaction : Ca(OH)2 + HNO3 → Ca(NO3)2 + H2O ?

Ca(OH)₂ + 2HNO₃ → Ca(NO₃)₂ + 2H₂O is the balanced chemical equation of the calcium hydroxide-nitric acid reaction.

2. What is a balanced chemical equation?

A balanced chemical equation is one in which the number of atoms of each element in the reactants equals the number of atoms of that element in the products. This is necessary for the law of conservation of mass to be satisfied.

3. What do you mean by stoichiometric coefficient.?

The number of molecules in a chemical species which participate in a chemical reaction is called its stoichiometric coefficient.

It calculates the ratio between the either sides of the chemical reaction.

4. Write the balanced equation for C3H8 + O2 → CO2 + H2O

C₃H₈ + 5O₂ → 3CO₂ + 4H₂O

5. Why do we need to balance chemical equations?

Balancing chemical equations is necessary to accurately represent chemical reactions. It also allows us to determine the stoichiometric relationships between the reactants and products, which can be useful for calculating the amount of reactants needed or the amount of products formed in a reaction.

6. How do you determine the stoichiometric coefficients in a balanced chemical equation?

The stoichiometric coefficients in a balanced chemical equation are determined by balancing the equation and ensuring that the number of atoms of each element is the same on both sides. The coefficients represent the ratios of the reactants and products in the reaction, so they must be in the lowest whole numbers possible.

7. What is the purpose of balancing chemical equations?

Balancing chemical equations ensures that the law of conservation of mass is obeyed. It means that the number of atoms of each element must be equal on both sides of the equation, reflecting that matter is neither created nor destroyed in a chemical reaction.

8. Why can't we change the subscripts in chemical formulas when balancing equations?

Changing subscripts in chemical formulas would alter the identity of the compounds involved. Subscripts represent the ratio of atoms in a molecule, and changing them would create a different substance altogether. We only adjust the coefficients (numbers in front of formulas) when balancing.

9. How does the law of conservation of mass apply to balancing chemical equations?

The law of conservation of mass states that matter cannot be created or destroyed in a chemical reaction. When balancing equations, we ensure that the number of atoms of each element is the same on both sides, reflecting this fundamental principle.

10. What are coefficients in a chemical equation and how are they used?

Coefficients are whole numbers placed in front of chemical formulas to indicate the number of molecules or formula units of that substance. They are adjusted during the balancing process to ensure equal numbers of atoms on both sides of the equation.

11. Can a balanced chemical equation have fractional coefficients?

While it's possible to use fractional coefficients to balance an equation, it's generally preferred to use whole numbers. If you end up with fractions, multiply all coefficients by the least common denominator to convert them to whole numbers.

12. What's the difference between reactants and products in a chemical equation?

Reactants are the starting substances in a chemical reaction, written on the left side of the arrow. Products are the substances formed as a result of the reaction, written on the right side of the arrow. The arrow indicates the direction of the reaction.

13. What is the significance of the arrow in a chemical equation?

The arrow in a chemical equation represents the direction of the reaction. It separates the reactants (on the left) from the products (on the right) and indicates that the reactants are being converted into the products.

14. What role do state symbols play in a balanced chemical equation?

State symbols (s, l, g, aq) indicate the physical state of each substance in the reaction. While they don't affect the balancing process, they provide important information about the conditions of the reaction and the nature of the substances involved.

15. What is the significance of a double arrow (⇌) in a chemical equation?

A double arrow indicates a reversible reaction, where the products can convert back into reactants under certain conditions. When balancing, treat it like a single arrow equation, ensuring both forward and reverse reactions are balanced.

16. What is the role of a catalyst in a chemical equation, and how does it affect balancing?

A catalyst is often written above the arrow in a chemical equation. It participates in the reaction but is neither consumed nor produced, so it doesn't affect the balancing process. However, it's important to note its presence in the equation.

17. How does balancing equations relate to stoichiometry?

Balancing equations is fundamental to stoichiometry, which deals with the quantitative relationships between reactants and products. A balanced equation provides the correct ratios of substances, allowing for calculations of amounts of reactants needed or products formed.

18. How does the concept of limiting reactants relate to balanced equations?

While limiting reactants don't affect the balancing process, a balanced equation is crucial for determining the limiting reactant. The balanced equation provides the stoichiometric ratios needed to calculate which reactant will be completely consumed first.

19. What's the difference between a skeleton equation and a balanced equation?

A skeleton equation shows the correct formulas of reactants and products but may not have the proper coefficients for balance. A balanced equation has the correct coefficients added to ensure equal numbers of atoms on both sides.

20. Why is it important to balance redox reactions in particular?

Balancing redox reactions is crucial because these reactions involve the transfer of electrons. Proper balancing ensures that the number of electrons lost by one species equals the number gained by another, maintaining electrical neutrality and mass conservation.

21. How do you balance equations involving diatomic elements?

Many elements exist as diatomic molecules in their natural state (e.g., H₂, O₂, N₂). When balancing, remember to use the diatomic form in the equation. This often requires using even coefficients for these elements.

22. What are half-reactions and how do they relate to balancing redox equations?

Half-reactions are separate equations showing the oxidation and reduction processes in a redox reaction. They are useful for balancing complex redox equations by allowing you to balance the oxidation and reduction parts separately before combining them.

23. What role does the periodic table play in balancing chemical equations?

The periodic table is crucial for identifying the elements in compounds and their properties. It helps in recognizing common oxidation states, which is particularly useful in balancing redox reactions and predicting products.

24. How do you approach balancing nuclear equations?

Nuclear equations are balanced differently from chemical equations. You must balance the mass numbers (total nucleons) and atomic numbers (protons) on both sides of the equation, often involving the emission or absorption of subatomic particles.

25. How does the concept of oxidation numbers help in balancing redox equations?

Oxidation numbers help identify which elements are being oxidized or reduced in a reaction. By tracking changes in oxidation numbers, you can determine how many electrons are transferred, which is crucial for balancing redox equations.

26. What is the difference between combination and decomposition reactions in terms of balancing?

Combination reactions involve two or more reactants forming a single product, while decomposition reactions involve a single reactant breaking down into multiple products. The balancing process is similar, but the number of species on each side of the equation differs.

27. How do you approach balancing combustion reactions?

For combustion reactions, typically involving a hydrocarbon reacting with oxygen, start by balancing carbon, then hydrogen, and finally oxygen. Often, the products are carbon dioxide and water, which helps in identifying the general structure of the balanced equation.

28. How does the presence of polyatomic ions affect the balancing process?

Polyatomic ions often remain intact during reactions. When balancing, treat each polyatomic ion as a single unit. This can simplify the process, as you don't need to balance each atom within the polyatomic ion separately.

29. What's the importance of balancing charge in ionic equations?

In ionic equations, the total charge on both sides must be equal. This is in addition to balancing the number of atoms. Failure to balance charge can result in an electrically imbalanced and physically impossible reaction.

30. How does the complexity of molecules affect the balancing process?

More complex molecules with multiple elements can make balancing more challenging. It often requires a systematic approach, balancing one element at a time, starting with the element that appears in the fewest number of compounds.

31. How do you approach balancing equations with multiple steps or intermediate products?

For multi-step reactions, balance each step separately, then combine the balanced equations. Ensure that any intermediate products cancel out in the overall equation if they're not part of the final products.

32. What are spectator ions, and how do they impact equation balancing?

Spectator ions are ions that don't participate in the reaction and appear unchanged on both sides of the equation. They can be omitted when writing net ionic equations, simplifying the balancing process.

33. What's the difference between balancing a molecular equation and an ionic equation?

A molecular equation shows all substances as molecules or compounds, while an ionic equation shows soluble ionic compounds as separated ions. Balancing an ionic equation requires considering individual ions, which can sometimes simplify the process.

34. How do you balance equations involving electron transfer in electrochemical cells?

For electrochemical cells, balance the half-reactions for oxidation and reduction separately, including electrons. Then combine the half-reactions, ensuring that the number of electrons lost equals the number gained.

35. What is the importance of balancing equations in predicting reaction yields?

A balanced equation provides the exact stoichiometric ratios of reactants and products. This is essential for calculating theoretical yields and determining the efficiency of a reaction by comparing actual yields to theoretical yields.

36. How do you approach balancing equations with unknown products?

When products are unknown, use your knowledge of reaction types and the reactants involved to predict possible products. Then write a skeleton equation and balance it. Experimental data may be needed to confirm the actual products.

37. How does the concept of mole ratios relate to balanced chemical equations?

The coefficients in a balanced equation represent the mole ratios of the substances involved. These ratios are fundamental to stoichiometric calculations, allowing conversion between moles or masses of different substances in the reaction.

38. What are the steps to balance a chemical equation using the algebraic method?

The algebraic method involves assigning variables to coefficients, writing equations based on the number of atoms of each element, and solving the resulting system of equations. This method is particularly useful for complex equations.

39. How do you balance equations involving fractional oxidation states?

For reactions with fractional oxidation states, multiply the entire equation by the least common denominator of the fractions to eliminate them. Then proceed with balancing as usual, using whole number coefficients.

40. What is the significance of a balanced equation in understanding reaction energetics?

A balanced equation is essential for calculating reaction enthalpies and free energy changes. The coefficients in the balanced equation directly relate to the stoichiometric amounts used in thermochemical calculations.

41. What are the common pitfalls to avoid when balancing chemical equations?

Common mistakes include changing subscripts instead of coefficients, forgetting to balance all elements, overlooking diatomic molecules, and not verifying that the final equation is balanced. Always double-check your work.

42. How does the presence of a precipitate affect the balancing of a chemical equation?

Precipitates, usually denoted with (s) for solid, don't change the balancing process. However, recognizing precipitate formation is crucial for writing net ionic equations, where spectator ions can be eliminated.

43. What is the relationship between balanced equations and the concept of limiting reagents?

Balanced equations provide the stoichiometric ratios needed to determine limiting reagents. By comparing the actual molar ratios of reactants to the ratios in the balanced equation, you can identify which reactant will be completely consumed first.

44. How do you balance equations involving complex ions?

Treat complex ions as single units, similar to polyatomic ions. Balance the complex ion as a whole, then ensure that the individual atoms within the complex are also balanced across the equation.

45. What is the importance of balancing equations in environmental chemistry?

Balanced equations are crucial in environmental chemistry for understanding and quantifying processes like acid rain formation, ozone depletion, and greenhouse gas emissions. They allow for accurate calculations of pollutant production and mitigation strategies.

46. How does the concept of equilibrium relate to balanced chemical equations?

In equilibrium reactions, the balanced equation represents the stoichiometric relationships at equilibrium. The coefficients in the balanced equation are used to write the equilibrium constant expression, a key tool in understanding reaction behavior.

47. What is the significance of balancing equations in biochemical reactions?

In biochemistry, balanced equations are essential for understanding metabolic pathways, enzyme kinetics, and cellular energetics. They allow for quantitative analysis of complex biological processes and the flow of matter and energy in living systems.

48. How do you approach balancing equations involving gases in non-standard conditions?

The balancing process remains the same regardless of conditions. However, when dealing with gases, it's important to note that the coefficients in the balanced equation represent molar ratios, which can be converted to volume ratios using gas laws if needed.

49. What is the role of oxidation numbers in balancing redox equations?

Oxidation numbers help identify which species are being oxidized or reduced. By calculating the change in oxidation numbers, you can determine the number of electrons transferred, which is crucial for balancing redox equations, especially using the half-reaction method.

50. How does the concept of stoichiometry extend from balanced equations to real-world applications?

Balanced equations form the foundation of stoichiometry, which is used in various real-world applications such as industrial chemical production, pharmaceutical manufacturing, and environmental monitoring. It allows for precise calculations of reactant needs and product yields.

51. What is the significance of balancing equations in understanding reaction mechanisms?

While a balanced equation shows the overall reaction, understanding reaction mechanisms often involves balancing multiple step-wise equations. This helps in identifying intermediates, transition states, and the detailed pathway of the reaction.

52. How do you balance equations involving multiple phases?

The presence of multiple phases (solid, liquid, gas, aqueous) doesn't change the balancing process. However, it's important to include phase labels (s, l, g, aq) in the final equation to provide a complete description of the reaction conditions.

53. What is the importance of balancing equations in analytical chemistry?

In analytical chemistry, balanced equations are crucial for quantitative analysis, titrations, and instrumental methods. They allow for the calculation of concentrations, determination of unknown quantities, and validation of analytical procedures.

54. How does the concept of rate laws relate to balanced chemical equations?

While rate laws are determined experimentally and may not directly correspond to the balanced equation, the balanced equation provides the foundation for understanding the reaction. It shows the stoichiometric relationships that inform initial hypotheses about rate laws.

55. What is the role of balancing equations in understanding coupled reactions?

In coupled reactions, where one reaction drives another, balancing each individual equation is crucial. The balanced equations allow for the analysis of how energy or electrons are transferred between the coupled processes, such as in ATP synthesis or electrochemical cells.

56. How does the principle of microscopic reversibility relate to balancing chemical equations?

Microscopic reversibility states that the mechanism of a reverse reaction follows the exact reverse path of the forward reaction. When balancing equations, this principle ensures that if the forward reaction is balanced, the reverse reaction will also be balanced, which is particularly important in understanding equilibrium processes.