Stoichiometric Calculations: Definition, Formula, Questions and Examples

Stoichiometry

Stoichiometry deals with the calculation of masses (sometimes volumes also) of the reactants and the products involved in a chemical reaction. Before understanding how to calculate the amounts of reactants required or the products produced in a chemical reaction, let us study what information is available from the balanced chemical equation of a given reaction.

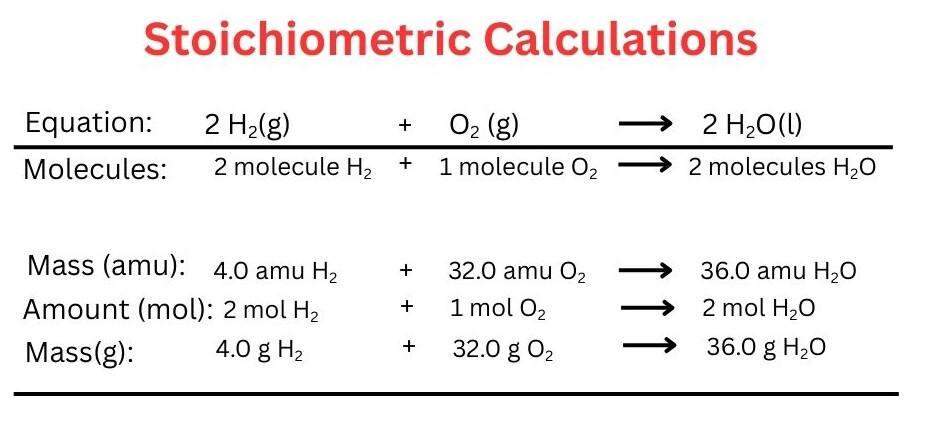
Stoichiometric Calculations

Step 1 Write down the correct formulas of reactants and products.

Step 2 Balance the number of atoms on both the reactant and product sides.

Step 3 Make the equation balanced.

The coefficients of atoms or molecules are stoichiometric coefficients.

Limiting Reagent

Quite often, one of the reactants is present in larger amount than the other as required according to the balanced equation. The amount of the product formed then depends upon the reactant which has reacted completely. This reactant which reacts completely in the reaction is called the limiting reagent. The reactant which is not consumed completely in the reaction is called excess reactant as the excess of this reactant is left unreacted.

Percentage Yield

Sometimes, experimentally, the reaction does not undergo 100% completion because of many factors that are involved in the actual industrial processes. So in such cases, we need the concept of % yield.

It is defined as the ratio of actual moles of product(s) formed to the number of moles that should have been theoretically formed assuming 100% completion of the reaction.

$\%$ yield $=\frac{\text { Actual number of moles formed }}{\text { Theoretical moles that should have formed }}$

Also Read:

• Gravimetric Analysis
• Law Of Equivalence

Recommended topic video on (Stoichiometric Calculations )

Some Solved Examples

Que 1: The minimum amount of O₂(g) consumed per gram of reactant is for the reaction : (Given atomic mass :Fe=56 O=16,Mg=24, P=31, C=12, H=1) )

1) $4 \mathrm{Fe}(\mathrm{s})+3 \mathrm{O}_2(\mathrm{~g}) \rightarrow 2 \mathrm{Fe}_2 \mathrm{O}_3(\mathrm{~s})$

2)$\mathrm{P}_4(\mathrm{~s})+5 \mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{P}_4 \mathrm{O}_{10}(\mathrm{~s})$

3)$\mathrm{C}_3 \mathrm{H}_8(\mathrm{~g})+5 \mathrm{O}_2(\mathrm{~g}) \rightarrow 3 \mathrm{CO}_2(\mathrm{~g})+4 \mathrm{H}_2 \mathrm{O}(\mathrm{I})$

4)$2 \mathrm{Mg}(s)+\mathrm{O}_2(g) \rightarrow 2 \mathrm{MgO}(\mathrm{s})$

Solution

The amount of Fe consumed for 3 moles of O₂ = 4 x 56 = 224g, Thus, the amount of O₂ consumed per gram of Fe = 3/224 g, Similarly, for other elements, we have: per gram P₄ required = 5/124 moles, per gram C₃H₈ required = 5/44 moles, per gram Mg required = 1/48 moles. Thus, the amount of O₂ is the minimum for Fe.

Hence, the answer is the option (1).

Que 2: For a reaction, $\mathrm{N}_2(\mathrm{~g})+3 \mathrm{H}_2(\mathrm{~g}) \rightarrow 2 \mathrm{NH}_3(\mathrm{~g})$ In which of the following reaction mixtures, H₂ is limiting reagent?

1) 56 g of $\mathrm{N}_2+10 \mathrm{~g}$ of $\mathrm{H}_2$

2) 35 g of $\mathrm{N}_2+8$ g of $\mathrm{H}_2$

3) 28 gof $\mathrm{N}_2+6 \mathrm{~g}$ of $\mathrm{H}_2$

4) 14 g of $\mathrm{N}_2+4$ g of $\mathrm{H}_2$

Solution

For:-

$\mathrm{N}_2(\mathrm{~g})+3 \mathrm{H}_2(\mathrm{~g}) \rightarrow 2 \mathrm{NH}_3(\mathrm{~g})$;

Identifying H₂ as a limiting reagent

(1)56 g of $\mathrm{N}_2+10 \mathrm{~g}$ of $\mathrm{H}_2$

$\frac{56}{28}=2$ mole $\quad \frac{10}{2}=5$ mole
Thus, in this case, 2 moles of N₂ will react with 6 moles of H₂, but only 5 moles of H₂ are available. Hence dihydrogen is the limiting reagent.

(2)35 g of $\mathrm{N}_2+8$ g of $\mathrm{H}_2$

$\frac{35}{28}=1.25$ mole $\quad \frac{8}{2}=4$ mole

(LR)

(3)28 g of $\mathrm{N}_2+6 \mathrm{~g}$ of $\mathrm{H}_2$ :- Reaction gets completed here

$\frac{28}{28}=1$ mole $\quad \frac{6}{2}=3$ mole

(4) 14 gof $\mathrm{N}_2+4$ gof $\mathrm{H}_2$

$\frac{14}{28}=0.5$ mole $\quad \frac{4}{2}=2$ mole

(LR)

Hence, the answer is the option (1).

Que 3: The ammonia (NH₃) released on the quantitative reaction of 0.6g, urea (NH₂CONH₂) with sodium hydroxide (NaOH) can be neutralized by:

1) 200 ml of 0.2 N HCl

2) 200 ml of 0.4 N HCl

3) 100 ml of 0.1N HCl

4) 100 ml of 0.2N HCl

Solution

2 × mole of Urea = mole of NH₃ ........(1)
mole of NH₃ = mole of HCl ........(2)

$\therefore$ mole of $\mathrm{HCl}=2 \times$ mole of Urea

mole of HCl =$2 \times \frac{0.6}{60}=0.02 \mathrm{~mol}$ ...(i)

[We know , mole = M X V = N X n X V]

$100 \mathrm{ml} \times 0.2 \mathrm{~N} \times 1=0.02 \mathrm{~mol}$ ...as (i).

Hence, the answer is the option(4).

Que 4. How many moles of CaCO₃ need to be heated to release 33.6 L of CO₂ at STP?

$\mathrm{CaCO}_3 \xrightarrow{\Delta} \mathrm{CaO}+\mathrm{CO}_2$

1) 1.5

2) 1

3) 2

4) 2.5

Solution

The chemical reaction is as follows:

$\mathrm{CaCO}_3 \xrightarrow{\Delta} \mathrm{CaO}+\mathrm{CO}_2$

Now moles of CO₂ released = 33.6 / 22.4
= 1.5 moles

$\therefore 1.5$ moles of $\mathrm{CaCO}_3$ gives 1.5 moles of $\mathrm{CO}_2$.

Hence, the answer is an option (1).

Que 5. Complete combustion of 1.80g of an oxygen-containing compound $\left(C_x H_y O_z\right)$ gave 2.64 g of CO₂ and 1.08 g of $\mathrm{H}_2 \mathrm{O}$. The percentage of oxygen in the organic compound is:

1) 50.33

2) 63.53

3) 53.33

4) 53.63

Solution

$
\begin{aligned}
& \mathrm{n}_{\mathrm{CO}_2}=\frac{2.64}{44}=0.06 \\
& \mathrm{n}_{\mathrm{c}}=0.06
\end{aligned}
$

weight of carbon $=0.06 \times 12=0.72 \mathrm{gm}$

$
\begin{aligned}
& \mathrm{n}_{\mathrm{H}_2 \mathrm{O}}=\frac{1.08}{18}=0.06 \\
& \mathrm{n}_{\mathrm{H}}=0.06 \times 2=0.12 \\
& \text { weight of } \mathrm{H}=0.12 \mathrm{gm} \\
& \therefore \text { Weight of oxygen in } \mathrm{C}_{\mathrm{x}} \mathrm{H}_y \mathrm{O}_{\mathrm{z}} \\
& =1.8-(0.72+0.12) \\
& =0.96 \text { gram }
\end{aligned}
$

$
\begin{aligned}
\% \text { weight of oxygen } & =\frac{0.96}{1.8} \times 100 \\
& =53.3 \%
\end{aligned}
$
Therefore, Option 3 is correct.

Practice more Questions from the link given below:

Conclusion

The interpretation of the coefficients as the number of moles is the basis of all stoichiometric calculations. Thus, to carry out stoichiometric calculations, the first step is writing the chemical equation for the reaction and then balancing it. The balanced chemical equation gives the stoichiometric coefficients which gives the proportion by moles. This method predicts yields, identifies limiting reagents, and determines required quantities in chemical reactions.