De Broglie Relationship
The twentieth century was a period that witnessed the quest to understand the dual nature of radiation and matter as well as new frontiers in quantum mechanics. De Broglie formulated the wave-particle duality, which challenged traditional theories about matter being made up of particles. In other words, like light exhibits particle-like and wave-like properties, particles including electrons can also exhibit wavelike characteristics.
This Story also Contains
- De-Broglie Wavelength- Quantum Leap:
- Bohr's model and de Broglie's relation: Number of standing waves made by an electron in nth Bohr orbit
- Some Solved Examples
- Practice More Questions From the Link Given Below:
- Conclusion:
Bohr's model of atom had limitations. So, there was need to develop some other model which could explain all the properties of atoms. Thereafter, Quantum mechanical model of the atom was given. There were some developments which led to the formulations of quantum mechanical model. These developments are:
- Dual behaviour of matter
- Heisenberg's uncertainty principle
De-Broglie Wavelength- Quantum Leap:
We studied before that the light possesses both wave and particle character i.e., dual character. de-Broglie in 1924 proposed that just like light, all the matter should exhibit both particle and wave-like properties i.e., dual behaviour. Just like light possesses wavelength and momentum, all the matter including electrons should have wavelength and momentum.
de-Broglie gave an expression for the wavelength and momentum of all material particles.
Wavelength($
\lambda
$) $=\mathrm{h} / \mathrm{mv}$
$
\begin{aligned}
\frac{1}{2} m v^2 & =K \cdot E \\
\lambda & =\frac{h}{\sqrt{2 K E \times M}}
\end{aligned}
$
It is given in terms of Planck’s constant through the formula:
$
\lambda=\frac{h}{m v}
$
In this formula 'h' represents Planck’s constant wherein 'p' stands for the momentum of a particular particle. 'm' is the mass of the particle and 'v' is the velocity of the particle. The product of mass and velocity is the momentum of the particle. $\mathrm{P}=\mathrm{mv}$
This equation has a certain aspect of wave-particle duality that describes quantum mechanics; nevertheless, electrons and atom particles exhibit wave properties. The equation presented by de Broglie is called the de Broglie equation proposing a method by which matter possesses wave characteristics thus affecting the fundamental approach toward the particle nature of matter in the atomic and subatomic domain.
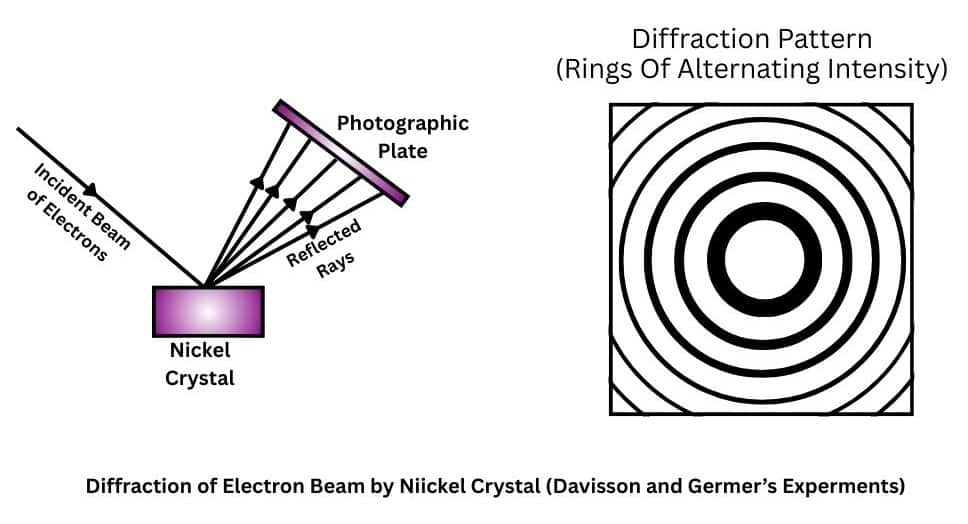
The de Broglie’s proposal was conferred after some experiments which confirmed both particle and wave nature of electron.
Particle Nature of Electron: Electron produced a spot of light on the zinc sulphide screen which is known as scintillation. Each striking electron produced only one spot. This suggests the particle nature of electron.
Wave Nature of Electron: This was confirmed by the diffraction patterns obtained which are a characteristic of waves.
It needs to be noted that according to de Broglie, every object in motion has a wave character. This wavelength is quite significant for the subatomic particles which have very small masses. The wavelengths associated with ordinary objects are however so short that their wave properties cannot be detected as they have large masses.
Also Check-
- NCERT Exemplar Class 11th Chemistry Solutions
- NCERT Exemplar Class 12th Chemistry Solutions
- NCERT Exemplar Solutions for All Subjects\
NCERT Chemistry Notes:
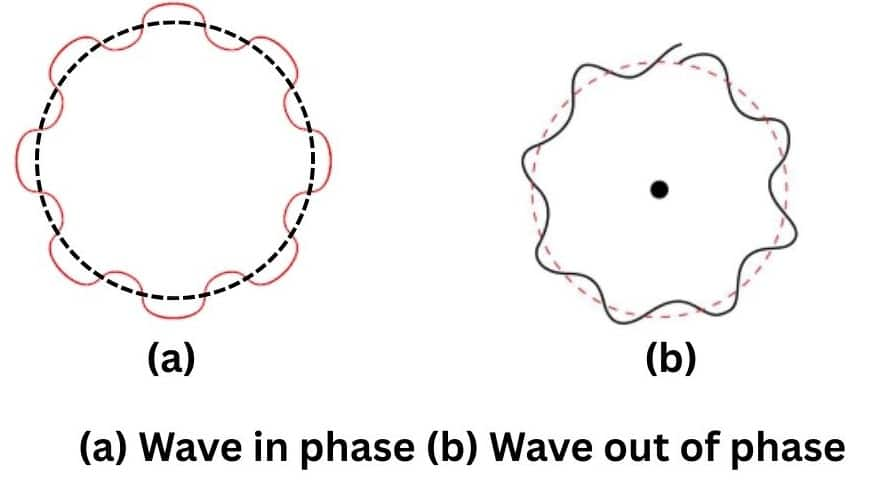
Bohr's model and de Broglie's relation: Number of standing waves made by an electron in nth Bohr orbit
According to the Bohr's model, the electron revolves around the nucleus in circular orbits. According to de Broglie concept, the electron is not only a particle but has a wave character. Thus, in order that the wave may be completely in phase, the circumference of the orbit must be equal to an integral multiple of wavelength ($
\lambda
$),
i.e., $2 \pi r=n \lambda$
Where 'r' is the radius of the orbit and 'n' is an integer.
But $\lambda=\mathrm{h} / \mathrm{mv}$.(de-Broglie equation)
Substituting this value of $
\lambda
$ in equation, we get
$
\begin{aligned}
2 \pi r & =\frac{n h}{m v} \\
O r & \\
m v r & =\frac{n h}{2 \pi}
\end{aligned}
$
Which is Bohr's postulate of angular momentum.
De-Broglie Equation-
de-Broglie proposed that just like light, matter should exhibit both particle and wave-like properties. This means that just as the photon has momentum as well as wavelength, electrons should also have momentum as well as wavelength, and he proposed the following mathematical relationship:
There is the de Broglie equation, which was given by Louis de Broglie and it defines the relationship between wavelength and momentum of the particle.
It is expressed as $\lambda=\mathrm{h} / \mathrm{mv}$. It is mathematically symbolized as $\lambda=\mathrm{h} / \mathrm{p}$.
Here h is Planck’s constant which is a natural constant. This equation implies that all particles, right from electrons to atoms, are regarded as having characteristics of both waves and particles. More precisely, it measures the wave properties of matter; it entails that particles with high momenta possess short wavelengths. This is in line with the de Broglie operation which is a substantial bar in quantum mechanical theory, which is intended to explain matter wave behaviour to give an account of the constitution of atomic and sub-atomic dimensions. This is because it retains several effects on so many science disciplines such as physics, chemistry as well as material science utilizing it to consistencies occurrences like electron interferences, atomic absorption, and movements of molecules among others.
$\lambda=\frac{h}{m v}=\frac{h}{p}=\frac{h}{\sqrt{2 m K E}}=\frac{h}{\sqrt{2 m q V}}$
where m is the mass of the particle, v is its velocity, p is its momentum,
KE is the Kinetic Energy of the particle,
V is the voltage across which the Charged particle having charge q is accelerated.
Also Read:
Recommended Topic Video on (De Broglie Relationship )
Some Solved Examples
Example 1: The de-Broglie wavelength of a particle of mass $
6.63 \mathrm{~g}
$ moving with a velocity of $100 \mathrm{~ms}^{-1}$ is:
1) $10^{-33} \mathrm{~m}$
2) $10^{-35} \mathrm{~m}$
3) $10^{-31} \mathrm{~m}$
4) $10^{-25} \mathrm{~m}$
Solution
As discussed in concept:
De-Broglie wavelength:
$\lambda=\frac{h}{m v}=\frac{h}{p}$
- wherein
where m is the mass of the particle
v: its velocity
p: its momentum
So,
$\begin{gathered}\lambda=\frac{6.625 \times 10^{-34}}{6.63 \times 10^{-3} \times 100} \\ \lambda=10^{-33} \mathrm{~m}\end{gathered}$
Hence, the answer is the option (1).
Example 2: A stream of electrons from a heated filament was passed between two charged plates kept at a potential difference V esu. If e and m are the charge and mass of an electron, respectively, then the value of $h / \lambda$ (where $
\lambda
$ is wavelength associated with electron wave) is given by
1) $\mathrm{meV}$
2) $2 \mathrm{meV}$
3) $\sqrt{m e V}$
4) $\sqrt{2 m e V}$
Solution:
We know that
De-Broglie wavelength:
$\lambda=\frac{h}{m v}=\frac{h}{p}$
- where
m is the mass of an electron.
v - its velocity.
p - its momentum.
$p=\frac{h}{\lambda}$
The kinetic energy of an electron in $\mathrm{eV}$
$\begin{aligned} K \cdot E & =\frac{p^2}{2 m} \\ e V & =\frac{p^2}{2 m}\end{aligned}$
where
V is the potential difference between two charge plates.
e is the charge of an electron.
Or $p=\sqrt{2 m e V}$
from equations (1) and (2)
$\frac{h}{\lambda}=\sqrt{2 m e V}$
Hence, the answer is an option (4).
Example 3:
The wavelength of an electron of kinetic energy $4.50 \times 10^{-29} \mathrm{~J}$ is $\qquad$ $\times 10^{-5} \mathrm{~m}$. (Nearest integer)
Given: mass of electron is $9 \times 10^{-31} \mathrm{~kg}, \mathrm{~h}=6.6 \times 10^{-34} \mathrm{Js}$
Solution:
$\begin{aligned} \lambda & =\frac{h}{\sqrt{2 \mathrm{mKE}}} \\ & =\frac{6.6 \times 10^{-34}}{\sqrt{2 \times 9 \times 10^{-31} \times 4.5 \times 10^{-29}}} \\ & =\frac{6.6 \times 10^{-34}}{9 \times 10^{-30}}=\frac{6.6}{9} \times 10^{-4} \\ & =\frac{66}{9} \times 10^{-5} \\ & =7.33 \times 10^{-5}\end{aligned}$
Hence, the answer is (7).
Practice More Questions From the Link Given Below:
Conclusion:
To sum up, de Broglie’s wavelength has had an overwhelming impact on how we understand the movement of matter at atomic and subatomic levels. By proposing that particles like electrons have a wave nature, Louis de Broglie changed the entire game of quantum mechanics and opened its doors to new revelations about the nature of particles and their interactions with each other. de-Broglie's relationship is not significant to macroscopic objects. This is because macroscopic objects have large masses and if we apply de-Broglie's relationship to large moving objects then the wavelength associated with the object is very short. Because wavelength is inversely proportional to mass. But the microscopic moving particles like electrons (small mass) have wavelength which is measurable. Therefore, de-Broglie's relationship holds good for such particles.
Frequently Asked Questions (FAQs)
In regards to the uncertainty principle, The de Broglie wavelength is related to the uncertainty principle, which postulates there are certain measurable physical properties where their values cannot both be known at once. It prognosis the wave-particle duality fundamental in quantum mechanics.
Real-life use is seen in electron microscopy to directly observe the atomic structure of objects, and in the aspects of quantum computing where the wave-particle duality of objects is employed in encoding information and encryption techniques.
The de Broglie wavelength is a concept used in quantum mechanics and it posits that particles in general, and electrons in specific, display wave behaviour. It postulates that every particle in motion, be it microscopic or minuscule, has a certain wavelength equal to the inverse of the momentum.
De Broglie wavelength can be calculated by using the following formula: Stir = h/p where Stir is the de Broglie wavelength, h is the Planck’s constant which is equal to 6.626 x10 – 34 Js, and p is the momentum which is defined by energy E divided by mc2 where m is the mass of the particle and c is the speed of light in the vacuum.
- New variables introduced as De Broglie wavelength (lambda) equals h/momentum.h is Planck’s constant and p is the momentum of the particle. The equation shows that those particles travelling with more momentum have short wavelengths.
In chemistry, they applied the concept of de Broglie’s wavelength to explain the motion of electrons around the nucleus or within molecules. It plays a vital role in understanding electron distribution, atomic structure, and various concepts related to chemical bonding.