Bohr's Model Of An Atom

Edited By Shivani Poonia | Updated on Jul 02, 2025 05:50 PM IST

Danish physicist Niels Bohr in the early years of the twentieth century endeavour to develop the progressive atom theory that not only revolutionized the outlook on atomic form but also formed the new quantum theories of modern times. Bohr’s version succeeded in overcoming the limitation of classical physics regarding the stability of atoms and the inherent line atomic spectra. At the center of Bohr’s model are several postulates suggested, in addition to the traditional tenets of classical mechanics.

This Story also Contains

Bohr's Model and its Postulates
Solved Examples Based On (Bohr's Postulate)-
Conclusion

Bohr's Model Of An Atom

In this article, we will cover the concept of Bohr's model and its postulates. This concept falls under the broader category of Atomic structure, which is a crucial chapter in Class 11 chemistry. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more.

Bohr's Model and its Postulates

Bohr’s model was proposed to be an improvement of the planetary model and was for the same reason developed; it included the electrons circling in orbits around the nucleus and in these orbits, they were only allowed to exist in certain fixed and discrete energy levels as opposed to the planetary model which predicted that electrons would move in free and smooth paths like planets around a star. These levels are quantized in the sense that they have been allocated specific values and an electron can only transfer from one level to another in quanta of energy equal to the difference between the two levels.

Bohr’s model also gave some explanation for the phenomenon that is known as stationary states, whereby the electrons in their stable orbits do not radiate as perceived by classical theories. This model was able to thoroughly account for the spectrum of hydrogen and also paved the way for something that turned out to be quantum mechanics. Even though there are significant weaknesses in Bohr’s model like the inability to explain the phenomena of multielectron atoms, this model is considered one of the important steps in the development of atomic theory as it gives a proper understanding of the electron behavior in an atom.

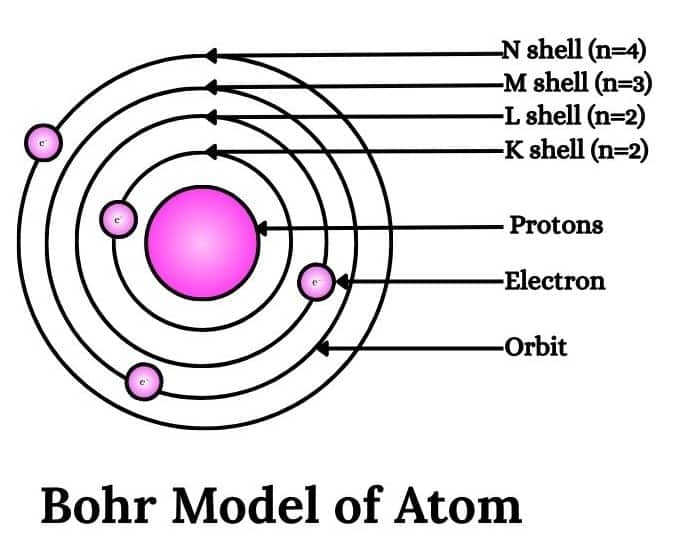
1. The electron in the hydrogen atom can move around the nucleus in a circular path of fixed radius and energy. These paths are called orbits, stationary states, or allowed energy states and are arranged concentrically around the nucleus. The force of attraction between the nucleus and an electron provides the centripetal force required by the electron to carry out the circular motion.

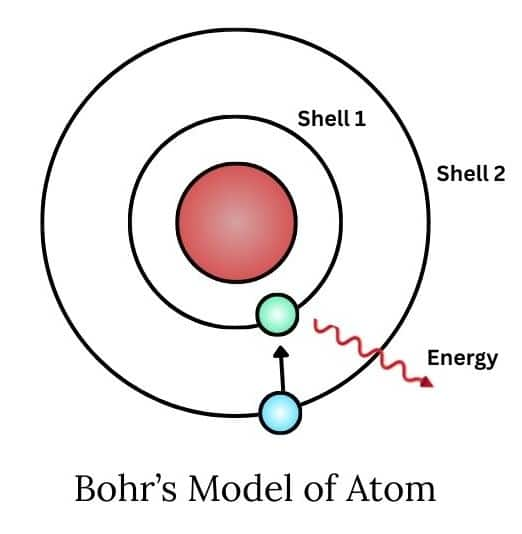
2. The energy of an electron in the orbit does not change with time. However, the electron will move from a lower stationary state to a higher stationary state when the required amount of energy is absorbed by the electron or energy is emitted when an electron moves from a higher stationary state to a lower stationary state

3. Energy can be absorbed or emitted when an electron transitions between two different orbits, and the frequency of the photon involved can be calculated using the formula:

|E1−E2|=hν

4. The angular momentum of an electron is quantized. In a given stationary state, it can be expressed as

L= mvr= nh/2$\pi$, n = orbit number

So only those energy states (or orbits) are allowed in which the above equation holds for the angular momentum.

Note: Bohr's model is only valid for Hydrogen species or electronic species that contain only a single electron.

Solved Examples Based On (Bohr's Postulate)-

Example 1: Which of the following statements is incorrect for Bohr's model of an atom?

1) (correct) It is valid for a multi-electronic species

2) The angular momentum of an electron is quantized

3) The centripetal force of attraction required for circular motion is provided by the electrostatic force of attraction between the electron and the nucleus

4) Orbits have fixed energy and are referred to as stationary states

Solution:

Bohr's model is valid for only uni-electronic species.

All other given statements given in the options are correct.

Hence, the answer is the option (1).

Example 2:

Which of the following is incorrect for Bohr's model of an atom?
1) (correct) It is valid for multi-electronic species.
2) The angular momentum of an electron is quantized.
3) The centripetal force of attraction required for circular motion is provided by the electrostatic force of attraction between the electron and the nucleus.
4) Orbits have fixed energy and are referred to as stationary energy.

Solution

Bohr's model is valid for electronic species only.

Hence, the answer is the option (1).

Conclusion

The version that was presented by Bohr was able to explain the spectral traces of hydrogen. Bohr’s model of the atom can be viewed as a scientifically critical stage in the paradigm shift from the old paradigm of classical physics to the new approaches of the modern quantum mechanics paradigm. While Bohr’s model had some problems, such as its inability to deliver a qualitative description of multielectron atoms and the quantization of angular momentum, it was useful in developing an early atomic model that helped accurately describe atomic spectra.

Also, check-

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download EBook

Frequently Asked Questions (FAQs)

1. What was Bohr's idea about the stability of the Atoms?

According to Bohr, the electrons reside in a specified region in a circle which is stable and hence can be referred to as stationary circular orbits because they do not emit energy due to centripetal force balancing the attractive force of the nucleus.

2. How did the Bohr explain the transition of electrons?

From emission and absorption spectra, discrete electron transition.

3. Name one limitation of the Bohr's model.

As Bohr's model applies to Hydrogen atoms only, that's why this model couldn't explain the multielectron atoms.

4. In atomic theory, what is Bohr's postulates?

The electron in the hydrogen atom can move around the nucleus in a circular path of fixed radius and energy. These paths are called orbits, stationary states, or allowed energy states and are arranged concentrically around the nucleus. The force of attraction between the nucleus and an electron provides the centripetal force required by the electron to carry out the circular motion.

5. What is Bohr's model of an atom?

Bohr's model of an atom is a theoretical representation proposed by Niels Bohr in 1913. It describes the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits at fixed energy levels. This model was a significant improvement over previous atomic models and helped explain the emission spectrum of hydrogen.

6. How does Bohr's model differ from earlier atomic models?

Bohr's model differs from earlier models like Thomson's "plum pudding" model and Rutherford's nuclear model by introducing the concept of fixed energy levels for electrons. It explains that electrons can only occupy specific, quantized energy levels and must absorb or emit energy to move between these levels.

7. What are the main postulates of Bohr's atomic model?

The main postulates of Bohr's atomic model are:

8. How does Bohr's model explain the stability of atoms?

Bohr's model explains atomic stability by proposing that electrons can only exist in specific, allowed energy levels. This prevents electrons from spiraling into the nucleus, as classical physics would predict. The discrete energy levels ensure that atoms maintain their structure and don't collapse.

9. What is the significance of the term "ground state" in Bohr's model?

The ground state in Bohr's model refers to the lowest energy state of an atom, where electrons occupy the innermost available energy levels. It's the most stable state of an atom and the one in which atoms are typically found under normal conditions.

10. What is the significance of the Bohr magneton in atomic physics?

The Bohr magneton is a fundamental unit of the electron's magnetic moment in Bohr's model. It's important in understanding the magnetic properties of atoms and their interactions with external magnetic fields.

11. How does Bohr's model explain the Balmer series in hydrogen's spectrum?

Bohr's model explains the Balmer series as transitions of electrons from higher energy levels to the second energy level (n=2) in hydrogen atoms. The model accurately predicts the wavelengths of these spectral lines, providing strong support for its validity.

12. How does Bohr's model contribute to our understanding of chemical reactions?

While Bohr's model is primarily an atomic model, its concept of electron shells and energy levels provides a basic framework for understanding chemical reactions. It helps explain why certain elements are more reactive than others and forms the basis for more advanced theories of chemical bonding and reactivity.

13. What is the significance of the Bohr effect in biochemistry?

While not directly related to Bohr's atomic model, the Bohr effect in biochemistry (named after Niels Bohr's father) describes how hemoglobin's oxygen affinity is affected by pH and CO2 concentration. It's an interesting example of how scientific principles can have unexpected applications in different fields.

14. What is the significance of the Bohr-van Leeuwen theorem?

The Bohr-van Leeuwen theorem, developed in part by Niels Bohr, demonstrates that classical physics cannot explain magnetism in materials. This realization highlighted the need for quantum mechanics to understand magnetic properties, further emphasizing the limitations of classical models like Bohr's.

15. How does Bohr's model relate to the concept of electron spin?

Bohr's original model doesn't include electron spin, which was discovered later. However, the model's success in explaining some spectral features and its limitations in explaining others helped pave the way for the discovery of electron spin as an additional quantum property.

16. What is the significance of the Bohr-Wentzel-Kramers-Brillouin (BWKB) approximation?

The BWKB approximation, which builds on concepts from Bohr's model, is a method for finding approximate solutions to linear differential equations with spatially varying coefficients. It's widely used in quantum mechanics and extends some of the semi-classical ideas present in Bohr's original model.

17. How does Bohr's model explain atomic spectra?

Bohr's model explains atomic spectra by proposing that electrons can transition between energy levels by absorbing or emitting specific amounts of energy. When electrons move from a higher to a lower energy level, they emit light with a specific wavelength, producing the characteristic spectral lines observed for each element.

18. What is the Bohr radius?

The Bohr radius is the distance between the nucleus and the electron in the first energy level (n=1) of a hydrogen atom according to Bohr's model. It's approximately 5.29 × 10^-11 meters and serves as a fundamental unit of length in atomic physics.

19. How does Bohr's model account for the different electron configurations in various elements?

Bohr's model accounts for different electron configurations by proposing that electrons fill energy levels from the innermost to the outermost, with each level having a maximum capacity. As atomic number increases, electrons occupy higher energy levels, leading to different electron configurations for different elements.

20. What is the main limitation of Bohr's model in explaining multi-electron atoms?

The main limitation of Bohr's model for multi-electron atoms is that it doesn't account for electron-electron repulsions. It works well for hydrogen and hydrogen-like ions but becomes increasingly inaccurate for atoms with more electrons, as it doesn't consider the complex interactions between multiple electrons.

21. How does Bohr's model relate to the concept of quantization?

Bohr's model directly incorporates the concept of quantization by proposing that electrons can only exist in specific, discrete energy levels. This quantization of energy states was a revolutionary idea that laid the groundwork for the development of quantum mechanics.

22. What is the Bohr frequency condition?

The Bohr frequency condition states that the frequency of light emitted or absorbed by an atom is equal to the difference in energy between two electron energy levels divided by Planck's constant. This condition explains the discrete nature of atomic spectra.

23. How does Bohr's model explain the Rydberg formula?

Bohr's model provides a theoretical basis for the empirical Rydberg formula, which describes the wavelengths of spectral lines in hydrogen. It explains that these lines result from electrons transitioning between different energy levels, with the energy differences corresponding to the observed spectral lines.

24. What role does angular momentum play in Bohr's model?

In Bohr's model, angular momentum is quantized, meaning it can only take on certain discrete values. This quantization is crucial for determining the allowed electron orbits and energy levels, and it helps explain why electrons don't spiral into the nucleus.

25. How does Bohr's model incorporate Planck's quantum theory?

Bohr's model incorporates Planck's quantum theory by proposing that electrons can only exist in discrete energy states and that transitions between these states involve the absorption or emission of specific quanta of energy, as described by Planck's equation E = hf.

26. What is the significance of the principal quantum number in Bohr's model?

The principal quantum number (n) in Bohr's model determines the energy level and size of the electron orbit. As n increases, the energy level and orbit radius increase, allowing for the description of electron shells and energy states in atoms.

27. How does Bohr's model explain the ionization energy of atoms?

Bohr's model explains ionization energy as the energy required to remove an electron from its highest occupied energy level to infinity. It predicts that ionization energy increases as electrons are removed from inner shells, which is consistent with experimental observations.

28. What is the relationship between Bohr's model and the periodic table?

Bohr's model helps explain the periodic table's structure by showing how electron configurations change as atomic number increases. It provides a basis for understanding the periodicity of element properties based on their electron arrangements.

29. How does Bohr's model account for the emission of photons?

In Bohr's model, photon emission occurs when an electron transitions from a higher energy level to a lower one. The energy difference between these levels determines the frequency (and thus the color) of the emitted photon, explaining the discrete spectral lines observed in atomic spectra.

30. How does Bohr's model explain the stability of certain electron configurations?

Bohr's model explains the stability of certain electron configurations, particularly those with filled shells, by proposing that these configurations represent lower energy states. This concept helps explain the chemical properties and reactivity of different elements.

31. What is the connection between Bohr's model and the concept of electron shells?

Bohr's model introduces the concept of electron shells, which are groups of energy levels that can hold a specific maximum number of electrons. This idea forms the basis for understanding electron configurations and chemical bonding.

32. What is the significance of the Bohr-Sommerfeld model?

The Bohr-Sommerfeld model is an extension of Bohr's original model that introduces elliptical orbits and additional quantum numbers. It attempts to explain more complex atomic spectra and provides a bridge between Bohr's model and modern quantum mechanics.

33. How does Bohr's model relate to the concept of electron probability distribution?

While Bohr's model depicts electrons in fixed circular orbits, it laid the groundwork for the concept of electron probability distribution. Modern quantum mechanics replaced these fixed orbits with probability clouds, but Bohr's energy levels still correspond to areas of high electron probability.

34. What is the role of the Coulomb force in Bohr's model?

The Coulomb force plays a crucial role in Bohr's model as the attractive force between the positively charged nucleus and the negatively charged electrons. It's balanced by the centripetal force of the orbiting electrons, determining the radii of the allowed orbits.

35. How does Bohr's model explain the concept of excited states?

In Bohr's model, excited states occur when electrons occupy energy levels higher than their ground state. These states are unstable, and electrons quickly return to lower energy levels, emitting photons in the process. This explains the emission of light by excited atoms.

36. What is the significance of the Bohr-Einstein relation in atomic physics?

The Bohr-Einstein relation connects the energy difference between two atomic states to the frequency of the photon emitted or absorbed during the transition. It's expressed as ΔE = hf, where h is Planck's constant and f is the frequency of the photon.

37. How does Bohr's model explain the concept of quantum jumps?

Bohr's model introduces the concept of quantum jumps, where electrons transition between energy levels instantaneously without existing in intermediate states. This idea challenges classical physics and is a key aspect of quantum behavior in atoms.

38. What is the relationship between Bohr's model and the uncertainty principle?

While Bohr's model predates the uncertainty principle, it inadvertently incorporates some aspects of it. The fixed electron orbits in Bohr's model imply a precise knowledge of both position and momentum, which the uncertainty principle later showed to be impossible.

39. How does Bohr's model contribute to our understanding of chemical bonding?

Bohr's model contributes to our understanding of chemical bonding by introducing the concept of electron shells and energy levels. This forms the basis for explaining valence electrons and how atoms combine to form molecules, even though more advanced models are needed for a complete understanding.

40. How does Bohr's model explain the photoelectric effect?

While Einstein explained the photoelectric effect, Bohr's model supports this explanation by showing that electrons in atoms exist in discrete energy levels. This quantization of energy aligns with the observation that light behaves as discrete packets (photons) in the photoelectric effect.

41. What is the connection between Bohr's model and spectroscopy?

Bohr's model provides a theoretical foundation for spectroscopy by explaining the discrete nature of atomic spectra. It shows how the unique spectral lines for each element result from electrons transitioning between specific energy levels, enabling element identification through spectral analysis.

42. How does Bohr's model relate to the concept of atomic orbitals?

While Bohr's model uses fixed circular orbits, it laid the groundwork for the concept of atomic orbitals. Modern quantum mechanics replaced these orbits with three-dimensional probability distributions (orbitals), but the energy levels in Bohr's model still correspond to the main energy levels in orbital theory.

43. How does Bohr's model contribute to our understanding of atomic size?

Bohr's model provides insights into atomic size by showing that electron orbits increase in radius as the principal quantum number increases. This helps explain why atoms of different elements have different sizes and why atoms in excited states are larger than those in the ground state.

44. What is the relationship between Bohr's model and the wave nature of electrons?

While Bohr's model doesn't explicitly incorporate the wave nature of electrons, it inadvertently hints at it. The allowed electron orbits in Bohr's model correspond to standing waves around the nucleus, a concept later formalized in de Broglie's matter wave theory and wave mechanics.

45. How does Bohr's model explain the concept of quantized angular momentum?

Bohr's model introduces the quantization of angular momentum by proposing that electrons can only exist in orbits where their angular momentum is an integer multiple of ħ (h-bar, or h/2π). This was a crucial step towards understanding the quantized nature of atomic properties.

46. What is the significance of the Bohr correspondence principle?

The Bohr correspondence principle states that quantum behavior must match classical behavior in the limit of large quantum numbers. This principle helped bridge the gap between classical and quantum physics, showing how quantum theories must reduce to classical results in appropriate limits.

47. What is the connection between Bohr's model and the fine structure constant?

The fine structure constant, a fundamental physical constant, appears in calculations related to Bohr's model. It's involved in determining the energy levels of hydrogen-like atoms and plays a crucial role in understanding the fine structure of spectral lines, which Bohr's original model couldn't fully explain.

48. How does Bohr's model contribute to our understanding of atomic clocks?

While atomic clocks use more advanced quantum mechanical principles, Bohr's model provides a foundational understanding of how atoms can serve as precise timekeepers. The model's description of discrete energy levels and transitions forms the basis for understanding the consistent frequency of atomic transitions used in atomic clocks.

49. What is the significance of the Bohr-Kramers-Slater (BKS) theory?

The BKS theory was an attempt by Bohr and colleagues to reconcile quantum theory with classical electromagnetism. Although ultimately unsuccessful, it played a crucial role in the development of quantum mechanics by highlighting the need for a more comprehensive theory of atomic behavior.

50. How does Bohr's model explain the concept of metastable states?

While Bohr's model doesn't directly address metastable states, it provides a framework for understanding them. Metastable states can be thought of as excited states with relatively long lifetimes, which can be visualized using Bohr's energy level diagrams.

51. What is the relationship between Bohr's model and the concept of quantum numbers?

Bohr's model introduces the principal quantum number (n) to describe electron energy levels. This laid the groundwork for the development of additional quantum numbers (l, m, s) in more advanced models, which are necessary to fully describe an electron's state in an atom.

52. How does Bohr's model contribute to our understanding of atomic absorption?

Bohr's model explains atomic absorption by showing that atoms can absorb photons with specific energies, causing electrons to jump to higher energy levels. This process is the reverse of emission and helps explain why atoms absorb light at the same frequencies they emit it.

53. How does Bohr's model relate to the concept of quantum confinement?

While Bohr's model predates the concept of quantum confinement, it introduces the idea of electrons being confined to specific energy levels within an atom. This notion of confinement and discrete energy states is fundamental to understanding quantum confinement in modern nanoscale systems.

54. What is the connection between Bohr's model and the development of laser technology?

Bohr's model, by explaining how atoms emit light through electron transitions between energy levels, laid the groundwork for understanding stimulated emission – the key principle behind lasers. The model's description of excited states and energy level transitions is crucial for grasping how lasers function.