Radial Nodes And Planar Nodes
Have you ever wondered what happens when electrons in an atom move through different energy levels or orbitals? How do certain regions in an orbital have zero probability of finding an electron, even though the atom is filled with these energetic particles? You can find all these answers by studying radial nodes and planar nodes. Radial nodes and planar nodes help explain the regions within an orbital where the probability of finding an electron is zero.
This Story also Contains
- Nodes
- Calculations of the Total Number of Nodes
- Some Solved Examples
- Practice More Questions With the Link Given Below:
- Conclusion
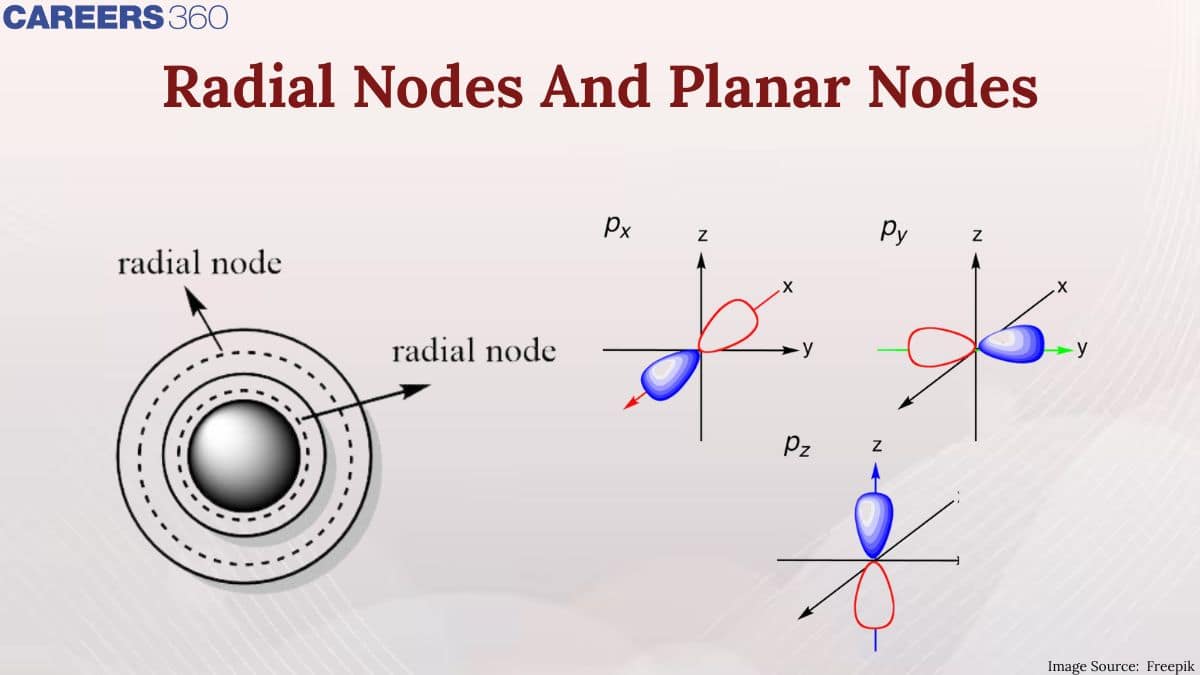
In chemistry, many experiments were conducted to understand the structure of atoms and also the subatomic particles. After the discovery of the subatomic particles, scientist were keen to know their position inside the atoms. How are electrons, protons, and neutrons arranged, and how does their specific position and arrangement make the atom stable? Are there specific points inside the atom where their probability of finding them is maximum, and where is the minimum or zero? To find out such answers, areas were found inside the atomic structure at the radial and angular planes, where the probability of electrons is zero.
Nodes
We know that $
\psi
$ has no physical significance. Instead, the square of its absolute value, i.e., $
|\psi|^2
$ has the significance as it gives the electron probability density of the electron at that point.
The variation of $
\psi
$ and $
|\psi|^2
$ at different distances (r) from the nucleus for 1s and 2s are shown in figure below:
.jpg)
We observe that the probability of 1s electron is found to be maximum near the nucleus and decrease as the distance from the nucleus increases. In case of 2s electrons, the probability is again maximum near the nucleus and then decreases to zero and increase again and then decreases as the distance from the nucleus increases. The intermediate region ( a spherical shell) where the probability is zero is called a nodal surface or simply node. Alternatively, the point where the wave function, $
\psi
$, changes sign from + to - represents a node. Thus, 2s orbital differs from 1s orbital in having one node within it. Similarly, 3s has two nodes. In general, any $
\text { ns }
$ orbital has $
(n-1)
$ nodes.
We will be talking about two types of nodes:
1. Planar Nodes
2. Radial Nodes
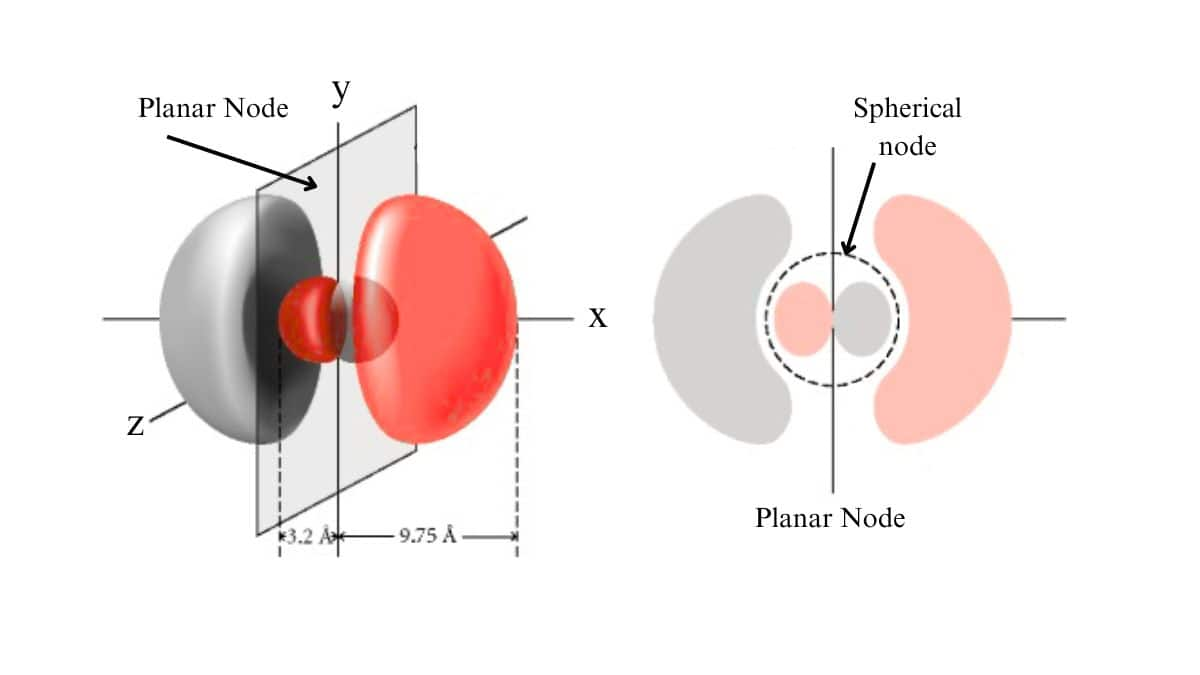
Planar Nodes
Planar nodes (or angular nodes) are flat, two-dimensional regions where the probability density of finding an electron is zero. They are associated with the angular part of the wave function. The number of planar nodes is equal to the azimuthal quantum number $l$. A planar node is also called the angular node, is also called the nodal plane.
For example:
- An s orbital ( $l=0$ ) has 0 planar nodes.
- A p orbital ( $l=1$ ) has 1 planar node.
- A d orbital ( $l=2$ ) has 2 planar nodes
.jpg)
Radial Node
In Context with atomic structure, nodes are the specific location, point, and area where the probability of an electron is zero. Nodes can be either Radial or Angular.
It has been discovered that, ns-orbitals have $(n-1)$ nodes, meaning that the number of nodes rises as the principal quantum number, n, grows.
Charge cloud diagrams are one way to depict these variations in probability densities.
A radial node is a spherical surface where the probability of finding an electron is zero. The number of radial nodes increases with the principle quantum number (n).
Radial nodes can be find out by the formula
Number of Radial nodes $=n-l-1=n-(l+1)$
where n is the principal quantum number, and l is the azimuthal quantum number.
(a) Calculating the number of radial nodes of 1s orbital;
In 1s orbital, the value of principal quantum number (n)= 1 and the value of Azimuthal quantum number (l)= 0
Number of Radial nodes =$n-1-1=1-0-1=0$
(b) Calculating the number of radial nodes of 2p orbital;
In 2p orbital, the value of principal quantum number (n)= 2 and the value of Azimuthal quantum number (l)= 1
Number of Radial nodes = $n-1-1=2-1-1=0$
(c) Calculating the number of radial nodes of 3d orbital;
In 2p orbital, the value of principal quantum number (n)= 3 and the value of Azimuthal quantum number (l)= 2
Number of Radial nodes = $n-1-1=3-2-1=0$

Calculations of the Total Number of Nodes
The total number of nodes is defined as the sum of the number of radial nodes and angular nodes.
Total number of nodes = Number of radial nodes + Number of Angular nodes
$\begin{aligned} & =(n-l-1)+1 \\ & =(n-1)\end{aligned}$
Total number of nodes $=(n-1)$
.jpg)
Example:
Calculating the total number of nodes of the 2s orbital:
In the 2s orbital, the value of the principal quantum number (n)= 2
The value of the Azimuthal quantum number (l)= 0
Total number of nodes = n-1= 2-1= 1
Also Read:
Recommended topic video on(Radial Nodes And Planar Nodes)
Some Solved Examples
Example 1: The number of radial nodes of the 3s and 2p orbitals is respectively
1) 2, 0
2) 0, 2
3) 1, 2
4) 2, 11
Solution
As we learn
For a given orbital, the number of radial nodes =n−l−1
For 3s orbital
n=3, l=0
Number of radial nodes = 3-0-1= 2
For 2p orbital
n = 2, l = 1
Number of radial nodes = 2-1-1 =0
Hence, the answer is option (1).
Example 2: The number of planar nodes in dx-y is
1) 0
2) 1
3) 2
4) 3
Solution
As we learn
No. of planar nodes = l where l is the azimuthal quantum number.
Number of planar nodes = l
For dxy, l = 2
Number of planar nodes = 2
Hence, the answer is option (3).
Example 3: The number of radial nodes and 2p orbitals is respectively
1) 2,0
2) 0,2
3) 1,2
4) 2,1
Solution
We know,
The number of Radial nodes for any electron in any orbital is given by the value of (n−ℓ−1)
For 3s electrons,$\mathrm{n}=3, \ell=0 \Rightarrow(\mathrm{n}-\ell-1)=3-0-1=2$
And for 2p electron,
$\mathrm{n}=2, \ell=1 \Rightarrow(\mathrm{n}-\ell-1)=2-1-1=0$
Hence, the answer is option (1).
Example 4: A certain orbital has no angular nodes and two radial nodes. The orbital is :
1) 3s
2) 3p
3) 2s
4) 2p
Solution
The number of angular nodes is given by ‘l’, i.e., one angular node for p orbitals, two angular nodes for ‘d’ orbitals, and so on.
Radial modes = n-l-1
The total number of nodes is given by (n–1), i.e., the sum of l angular nodes and (n – l – 1) radial nodes.
Given
A certain orbital has no angular nodes and two radial nodes,
So, l=0,
It will be s orbital; it does not have angular nodes.
And
Radial nodes = 2
n – l –1 = 2
n – 0 – 1 = 2
n= 3
So, the orbital will be 3s.
Hence, the answer is option (1).
Example 5: A certain orbital has no angular nodes and two radial nodes. The orbital is :
1) 3s
2) 2p
3) 2s
4) 2p
Solution
the number of angular nodes is given by ‘l’, i.e., one angular node for p orbitals, two angular nodes for ‘d’ orbitals, and so on.
Radial nodes = n-l-1
The total number of nodes is given by (n–1), i.e., the sum of l angular nodes and (n – l – 1) radial nodes.
Given
A certain orbital has no angular nodes and two radial nodes,
So, l=0,
It will be s orbital, it does not have angular nodes.
And
Radial nodes = 2
n – l –1 = 2
n – 0 – 1 = 2
n= 3
So, the orbital will be 3s.
Hence, the answer is option (1).
Example 6: For $2 P_x$ and $3 d_{x y}$ nodal plane are respectively [JEE Main 2024]
1) YZ plane & YZ, XY Planes
2) YZ plane & XZ, XY Planes
3) XZ plane & XZ, YZ Planes
4) YZ plane & XZ, YZ Planes
Solution:
In 2Px orbital Nodal Plane is YZ plane and in 3dxy orbital nodal planes are XZ and YZ.
Hence, the answer is the option (3).
Practice More Questions With the Link Given Below:
| Radial nodes and planar nodes practice question and MCQs |
| Quantum Numbers planar nodes practice question and MCQs |
Also Check
Conclusion
So, it can be noted that radial and angular nodes are quite significant, and its concepts are required to explain atomic structure as well as electron properties. Radial nodes describe volumes within the electron cloud inside an atom where the electron density is most likely to be at its lowest and is involved in the determination of both the size of the atomic orbitals and their shapes. Angular nodes, on the other hand, are points on the surfaces of the atoms where the Electron Density Distribution preference along certain axes is also not present and thus influences the orientation or even the symmetry of the orbitals. Taken together, all of these nodes provide the base from which one can conceptualize how electrons are divided within an atom and, therefore, predict chemical bonding or reactivity. Once again, an understanding of the meaning of radial and angular nodes adds more clarity to different happenings within atomic structures and the factors involved in different forms of science.
Frequently Asked Questions (FAQs)
In Atomic structure , Radial node is used to find the probability of electron around the nucleus.
A radial node is a spherical surface where the probability of finding an electron is zero. The number of radial nodes increases with the principle quantum number (n).
An angular node is a plane that passes through the nucleus. The angular node is equal to the azimuthal quantum number (l).