Speed of Electromagnetic Radiation And EM Radiation

Nature of Electromagnetic Radiation

James Maxwell (1870) gave the explanation about the interaction between the charged bodies and the behaviour of electric and magnetic fields on macroscopic level.

Light and other forms of radiant energy that propagates in the form of waves are called electromagnetic waves or electromagnetic radiations. These waves are produced by a charged body moving in a magnetic field or a magnet moving in an electric field. Maxwell first revealed that light waves are associated with oscillating electric and magnetic character.

The main points of this theory are as follows:

• The energy is emitted from any source (like the heated rod through which electric current is passed) continuously in the form of radiations and is called the radiant energy.
• The radiations consist of electric and magnetic fields oscillating perpendicular to each other and both perpendicular to the direction of propagation of the radiation.
• The radiations possess wave character and travel with the velocity of light (i.e., nearly$
  3 \times 10^8 \mathrm{~m} / \mathrm{sec}
  $).

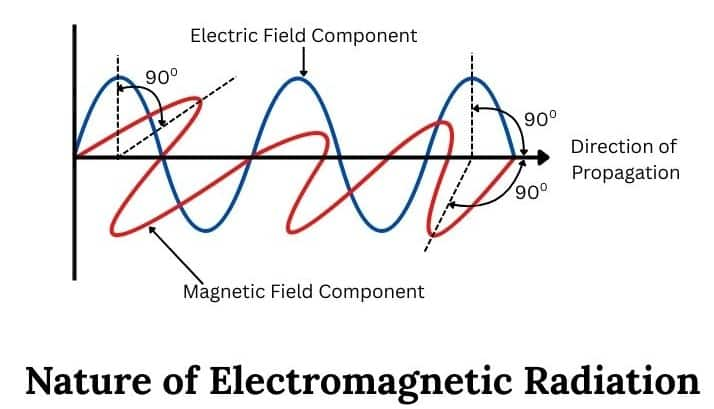
• Electromagnetic waves do not require any medium for their propagation. That means these waves can propagate in vacuum.
• There are many types of elecrtromagnetic radiations which differ from one another in terms of their frequency and wavelength. These all types of electromagnetic radiations constitute what is known as electromagnetic spectrum.

Also Read -

• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 12 Chemistry
• NCERT Solutions for All Subjects

Parameters to Define Wave

There are several parameters required to characterize or define a wave. These parameters are defined below:

1. Wavelength ($\lambda$): It is the distance travelled by the wave during one complete oscillation.

The maxima are called crests and the minima are called Troughs. Alternatively, the distance between two consecutive crests or two consecutive troughs is also called the wavelength.

2. Time Period (T): It is the time required for one complete oscillation or one complete cycle by a wave.

3. Frequency ($\nu$) : It is the number of waves produced by the source in one second

It is the inverse of the period. Its S.I unit is Hertz (Hz).
$v=1 / T$

4. Velocity (v): It is the distance travelled by the wave in one second.

$
\text { Velocity }=\text { Frequency } X \text { Wavelength }
$

$
C=v \lambda
$

The speed of all the different components of light is the same i.e. they travel with the speed of $3 \times 10^8 \mathrm{~m} / \mathrm{s}$. Their frequency and wavelength are different.

5. Wave number ($\bar{v}$): It is the inverse of the wavelength. It can also be defined as the number of wavelengths present in unit length.

$\bar{v}$ $
=1 / \lambda
$

Also Check-

• NCERT Exemplar Class 11th Chemistry Solutions
• NCERT Exemplar Class 12th Chemistry Solutions
• NCERT Exemplar Solutions for All Subjects

Electromagnetic Spectrum :

The arrangement of the various types of electromagnetic radiations in the order of their increasing wavelengths or decreasing frequencies is known as electromagnetic spectrum.

The rays present on the left extreme of the spectrum have the greatest frequency, least wavelength, and the greatest energy, As the frequency increases, wavelength decreases, and energy increases.

Also Study:

• Planck's Quantum Theory
• Photoelectric Effect

Recommended Topic Video on (Electromagnetic Radiation)

Solved Examples-

Example 1: Which of the following EM radiation lies in the highest energy region?

1) UV rays
2) X-rays
3) γ−rays
4) Radio waves

Solution:
Wavelength of electromagnetic radiation:

Radiowave - greater than 10⁹ Angstrom
Microwave -10⁹ to 10⁶ Angstrom
Infrared - 10⁶ to 7000 Angstrom

Visible light- 7000 to 40000 Angstrom

Ultraviolet - 4000 to 10 Angstrom
X-rays - 10 to 0.1 Angstrom
Gamma rays - less than 0.1 Angstrom

Now, The Relation between Energy and Wavelength of EM Waves,
E=hν=hc/λ

E∝1/λ

The energy of the EM wave is in the following order:

γ rays > X - rays > UV rays> visible rays> Infrared rays> microwave > radio wave

Hence, the answer is the option(3).

Example 2: The value of Planck's constant is 6.63×10⁻³⁴J-s. The velocity of light is 3.0×10⁸ ms⁻¹. Which value is closest to the wavelength in nanometers of a quantum of light with a frequency of 8×10¹⁵s⁻¹
1) 3×10⁷
2) 2×10⁻²⁵
3) 5×10⁻¹⁸
4) 37.5

Solution:
We know that,
$\begin{aligned} & \mathrm{v}=\mathrm{c} \lambda \Rightarrow \lambda=\mathrm{c} / \mathrm{v} \\ & \Rightarrow \lambda=\mathrm{c} / \mathrm{v}=3 \times 10^8 / 8 \times 10^{15}=3.75 \times 10^{-8} \mathrm{~m}=3.75 \times 10^{-8} \mathrm{x} \\ & 10^9 \mathrm{~nm}=4 \times 10 \mathrm{~nm}\end{aligned}$

Hence, the answer is the option (4).

Example 3: Assertion: Electromagnetic waves can be polarised.

Reasoning: The direction of the electric field vector in an electromagnetic wave determines its polarization.

1) Both assertion and reasoning are true, and the reasoning is the correct explanation of the assertion.

2) Both assertion and reasoning are true, but the reasoning is not the correct explanation of the assertion.

3) The assertion is true, but the reasoning is false.

4)Both assertion and reasoning are false.

Solution:

An electromagnetic wave consists of oscillating electric and magnetic fields that are perpendicular to each other and the direction of propagation of the wave. The direction of the electric field vector in an electromagnetic wave determines its polarization. If the electric field vector oscillates in a single plane, the wave is said to be polarised. Electromagnetic waves can be polarised by using a polarising filter, which transmits only the waves that have their electric field vectors oriented in a particular direction. Therefore, both the assertion and reasoning are true, and the reasoning is the correct explanation of the assertion.

Hence, the answer is the option (1).

Example 4:

Following figure shows spectrum of an ideal black body at four different temperatures. The number of correct statement/s from the following is________________. [JEE Main 2023]

A. $\mathrm{T}_4>\mathrm{T}_3>\mathrm{T}_2>\mathrm{T}_1$

B. The black body consists of particles performing simple harmonic motion.

C. The peak of the spectrum shifts to shorter wavelength as temperature increases.

D. $\frac{T_1}{v_1}=\frac{T_2}{v_2}=\frac{T_3}{v_3} \neq$ constant

E. The given spectrum could be explained using quantisation of energy.

1) 2

2) 3

3) 4

4) 1

Solution:

(A) $\mathrm{T}_4>\mathrm{T}_3>\mathrm{T}_2>\mathrm{T}_1$

(C) The peak of the spectrum shift to shorter wavelength of temp. Inc.

Hence, the answer is the option (1).

Practice More Questions From the Link Given Below:

Conclusion

We discussed the electromagnetic wave theory, in which we understand the relationship between electricity and magnetism. The electromagnetic wave emits energy and is hence also called electromagnetic radiation. Understanding electromagnetic waves allows us to predict other phenomena related to electricity and other electrical transformations. The Generators, Transformers, and other wireless devices principles are directly or indirectly based on electromagnetic wave theory.