Components of a Vector Along and Perpendicular to another Vector

Let's first revise the vector concept before knowing about the component of the vector. A quantity that has magnitude as well as a direction in space and follows the triangle law of addition is called a vector quantity, e.g., velocity, force, displacement, etc. in real life we use vectors for tracking objects that are in motion, and localization of places and things.

JEE Main: Study Materials | High Scoring Topics | Preparation Guide

JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs

This Story also Contains

1. Projection of vector
2. Scalar Projection
3. Solved Examples

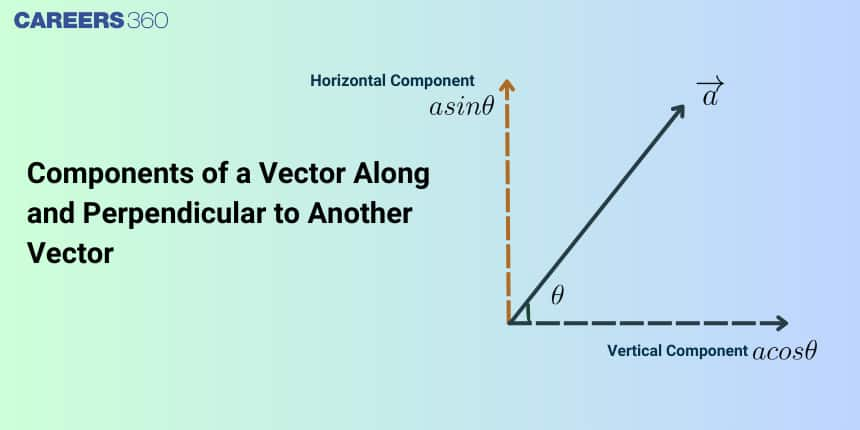
In this article, we will cover the concept of Finding Components of a vector Along and Perpendicular to another Vector. This topic falls under the broader category of Vector Algebra, which is a crucial chapter in Class 11 Mathematics. This is very important not only for board exams but also for competitive exams, which even include the Joint Entrance Examination Main and other entrance exams: SRM Joint Engineering Entrance, BITSAT, WBJEE, and BCECE. A total of ten questions have been asked on this topic in JEE Main from 2013 to 2023 including one in 2018 and one in 2023.

Projection of vector

The vector projection is of two types: Scalar projection which tells about the magnitude of vector projection and the other is the Vector projection which says about itself and represents the unit vector.

Scalar Projection

Let a→ and b→ be two vectors then,

Projection of a→ on b→=a→⋅b→|b→|=a→⋅b→|b→|=a→⋅b^
Projection of b→ on a→=a→⋅b→|a→|=b→⋅a→|a→|=b→⋅a^

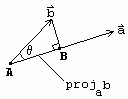
Vector Projection
Let a→ and b→ be two vectors represented by OA→ and OB→ respectively and let ⊖ be the angle between a→ and b→. Then,

b→=OM→+MB→
Also,

OM→=(OM)a^=(OBcos⁡θ)a^==(|b→|cos⁡θ)a^=((a→⋅b→)|a→|)a^=((a→⋅b→)|a→||a→|)a→[∵a^=a→|a→|]=((a→⋅b→)|a→|2)a→

As,

b→=OM→+MB→MB→=b→−OM→=b→−((a→⋅b→)|a→|2)a→
Thus, the components of b→ along and perpendicular to a→ are ((a→⋅b→)|a→|2)a→ and b→−((a→⋅b→)|a→|2)a→, respectively.

Solved Examples

Example 1: The length of the projection of the line segment joining the points (5,−1,4) and (4,−1,3) on the plane, x+y+z=7 is : [JEE MAINS 2018]
Solution

Projection of a line segment on a line - Projection of the line segment joining the points P(x1,y1,z1) and Q(x2,y2,z2) on a line having direction cosines (l,m,n) is (x2−x1)l+(y2−y1)m+(z2−z1)n

- wherein

Here PQ is the projection
Also PQ=BC

AC=AB^⋅BC^=(i^+k^)⋅(i^+j^+k^3)=2/3
Also AB=2

AB=AC2+BC2=2=4/3+BC2BC2=2/3
Example 2: Let ABCD be a parallelogram such that AB→=q→,AD→=p→ and ∠BAD be an acute angle. If r→ is the vector that coincides with the altitude directed from the vertex B to the side AD, then r→ is given by Solution:

r→=BA→+AQ→

=−q→+ projection of BA→ across AD→=−q→+(p→⋅q→)p→(p→⋅p→)

Projection of vector b on vector a -

b→cos⁡Θ=a→⋅b→|a→|

Example 3: Let u→,v→,w→ be such that |u→|=1,|v→|=2,|w→|=3. If the projection v→ along u→ is equal to that of w→ along u→ and v→,w→ are perpendicular to each other then |u→−v→+w→| equals

Solution:

Projection of vector b on vector a b→cos⁡θ=a→⋅b→|a→|

Scalar Product of two vectors -
a→⋅b→>0 an acute angle
a→⋅b→<0 an obtuse angle
a→⋅b→=0 a right angle
- wherein
Θ is the angle between the vectors a→ and b→

v→⋅u→|u→|=w→⋅u→|u→|⇒v→⋅u→=w→⋅u→
Also, ⇒v→⋅w→=0

⇒|u→v→+w→|=|u→|2+|v→|2+|w→|2=1+4+9=14

Example 4:

The magnitude of the projection of vector 2i^+3j^+k^ on the vector perpendicular to the plane containing the vectors i^+j^+k^ and i^+2j^+3k^ is

Solution

Projection of vector b on vector a -

$
\vec{b} \cos \Theta=\frac{\vec{a} \cdot \vec{b}}{|\vec{a}|}

Normal vector to the plane containing vector i^+j^+k^
and i^+2j^+3k^ is

n^=(i^+j^+k^)×(i^+2j^+3k^)n^=i^−2j^+k^
Projection of 2i^+3j^+k^ on n^

=|(2i^+3j^+k^)(i^−2j^+k^)1+4+1|

=36=32

Example 5: The distance of the point having position vector −i^+2j^+6k^ from the straight line passing through the point ( 2, 3 , -4 ) and parallel to the vector, 6i^+3j^−4k^ is :

Solution

Projection of vector b on vector a -b→cos⁡Θ=a→⋅b→|a→|

Point P(-1,2,6) & A(2,3,-4)

and n→=6i^+3j^−4k^

x→=6i^+3j^−4k^

PD2=AP2−AD2

AD=|AP→⋅n→|n→|

AD=|(3i^+j^−10k^)⋅(6i^+3j^−4k^)|6i^+3j^−4k^|=61PD=110−61=7

Summary

Understanding vector components is fundamental for analyzing and manipulating vectors. Components provide a clear and systematic way to express the influence of a vector along specific axes or directions within a coordinate system. This concept is essential for solving equations, performing calculations, and interpreting physical phenomena accurately