Dot Product of Two Vectors - Properties and Examples

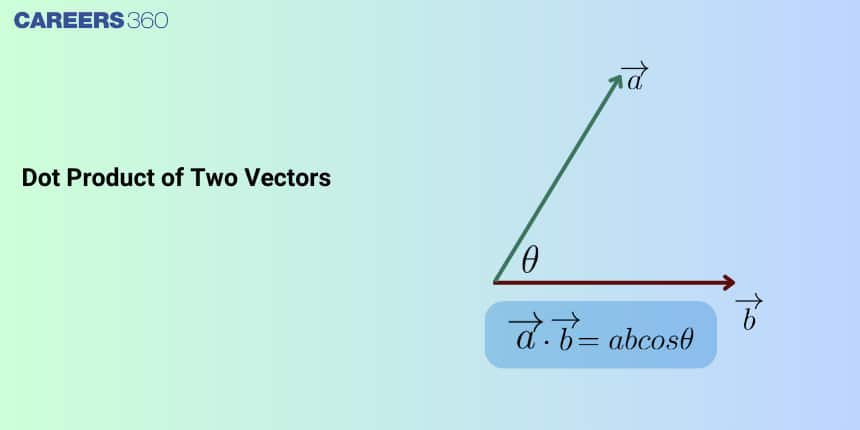
What is the Dot Product (Scalar Product) of Two Vectors?

The dot product of two vectors, also called the scalar product, is defined as the product of the magnitudes of the two vectors and the cosine of the angle between them. It is one of the most important concepts in vector algebra and is widely used to find angles between vectors, calculate work done, determine projections, and solve problems in physics and engineering.

If $\vec{a}$ and $\vec{b}$ are two non-zero vectors, then their dot product is denoted by $\vec{a}\cdot\vec{b}$

Meaning of Dot Product in Vector Algebra

The dot product tells us how much one vector acts in the direction of another. If the vectors point in the same direction, the dot product is maximum. If they are perpendicular, the dot product becomes zero. This makes the scalar product extremely useful in checking perpendicularity and parallelism of vectors.

Dot Product Formula

If $\vec{a}$ and $\vec{b}$ are two non-zero vectors and $\theta$ is the angle between them, then the dot product is given by $\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta \quad (0\leq\theta\leq\pi)$

where

• $|\vec{a}|$ is the magnitude of vector $\vec{a}$

• $|\vec{b}|$ is the magnitude of vector $\vec{b}$

• $\theta$ is the angle between $\vec{a}$ and $\vec{b}$

Key Points about the Scalar Product

• The result of a dot product is always a scalar quantity.

• It depends on both the magnitudes of the vectors and the angle between them.

• It plays a central role in topics like projections, work-energy theorem, and angle calculation between vectors.

Observations on Dot Product of Two Vectors

The dot product of two vectors gives important geometric and algebraic information. From the formula $\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$, we can make the following key observations:

1. $\vec{a}\cdot\vec{b}$ is always a real number.

2. $\vec{a}\cdot\vec{b}$ is positive if $\theta$ is acute.

3. $\vec{a}\cdot\vec{b}$ is negative if $\theta$ is obtuse.

4. $\vec{a}\cdot\vec{b}$ is zero if $\theta=90^\circ$, which means the vectors are perpendicular.

5. $\vec{a}\cdot\vec{b}\leq|\vec{a}||\vec{b}|$, with equality when the vectors are parallel and in the same direction.

These observations make the dot product a powerful tool to check the nature of the angle between two vectors.

Dot Product of Two Vectors in Component Form

In vector algebra, vectors are often expressed using unit vectors $\hat{i},\hat{j},\hat{k}$.
If $\vec{a}=a_1\hat{i}+a_2\hat{j}+a_3\hat{k}$ and $\vec{b}=b_1\hat{i}+b_2\hat{j}+b_3\hat{k}$ then the dot product of two vectors is given by $\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2+a_3b_3$

This form is extremely useful for numerical problems and coordinate geometry.

Derivation of Dot Product Formula in Component Form

Start with $\vec{a}\cdot\vec{b} = (a_1\hat{i}+a_2\hat{j}+a_3\hat{k})\cdot(b_1\hat{i}+b_2\hat{j}+b_3\hat{k})$

Expand using distributive property: $\vec{a}\cdot\vec{b} = a_1\hat{i}\cdot(b_1\hat{i}+b_2\hat{j}+b_3\hat{k})+a_2\hat{j}\cdot(b_1\hat{i}+b_2\hat{j}+b_3\hat{k})+a_3\hat{k}\cdot(b_1\hat{i}+b_2\hat{j}+b_3\hat{k})$

$= a_1b_1(\hat{i}\cdot\hat{i}) + a_1b_2(\hat{i}\cdot\hat{j}) + a_1b_3(\hat{i}\cdot\hat{k}) + a_2b_1(\hat{j}\cdot\hat{i}) + a_2b_2(\hat{j}\cdot\hat{j}) + a_2b_3(\hat{j}\cdot\hat{k})+ a_3b_1(\hat{k}\cdot\hat{i}) + a_3b_2(\hat{k}\cdot\hat{j}) + a_3b_3(\hat{k}\cdot\hat{k})$

Since $\hat{i}\cdot\hat{i}=1,\hat{j}\cdot\hat{j}=1,\hat{k}\cdot\hat{k}=1$ and $\hat{i}\cdot\hat{j}=\hat{j}\cdot\hat{k}=\hat{k}\cdot\hat{i}=0$,

we get $\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2+a_3b_3$

This is the standard dot product formula in Cartesian form.

Properties of Dot (Scalar) Product

These properties are essential for solving vector algebra problems and simplifying expressions:

1. Commutative Property
   $\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}$

2. Distributive Property
   $\vec{a}\cdot(\vec{b}+\vec{c})=\vec{a}\cdot\vec{b}+\vec{a}\cdot\vec{c}$

3. Scalar Multiplication
   $(m\vec{a})\cdot\vec{b}=m(\vec{a}\cdot\vec{b})=\vec{a}\cdot(m\vec{b})$

4. Product of Two Scalars with Vectors
   $(l\vec{a})\cdot(m\vec{b})=lm(\vec{a}\cdot\vec{b})$

These properties make the dot product algebraically consistent and easy to manipulate.

Important Results Using Dot Product

For any two vectors $\vec{a}$ and $\vec{b}$:

(i) Square of Sum and Difference of Vectors

$|\vec{a}\pm\vec{b}|^2
=|\vec{a}|^2+|\vec{b}|^2\pm2\vec{a}\cdot\vec{b}
=|\vec{a}|^2+|\vec{b}|^2\pm2|\vec{a}||\vec{b}|\cos\theta$

This formula is widely used to find angles between vectors and solve geometry-based vector problems.

(ii) Product of Magnitudes of Sum and Difference

$|\vec{a}+\vec{b}|\cdot|\vec{a}-\vec{b}|=|\vec{a}|^2-|\vec{b}|^2$

(iii) Condition for Like Vectors

$|\vec{a}+\vec{b}|=|\vec{a}|+|\vec{b}|\Rightarrow \vec{a}$ and $\vec{b}$ are like vectors

This means the vectors are parallel and in the same direction.

(iv) Condition for Perpendicular Vectors

$|\vec{a}+\vec{b}|=|\vec{a}-\vec{b}|\Rightarrow \vec{a}\perp\vec{b}$

This gives a neat and quick test for orthogonality using dot product concepts.

Angle Between Two Vectors Using Dot Product

The angle between two vectors is one of the most important applications of the dot product in vector algebra. It helps us understand how two vectors are oriented with respect to each other in space. The cosine of the angle between two vectors is equal to the dot product of the vectors divided by the product of their magnitudes. This concept is widely used in maths, physics, engineering, and coordinate geometry.

From the dot product formula, $\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$

we get, $\cos\theta=\dfrac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}$ and hence, $\theta=\cos^{-1}\left(\dfrac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}\right)$

This is the standard formula to find the angle between two vectors.

Angle Between Two Vectors in Component Form

If $\vec{a}=a_1\hat{i}+a_2\hat{j}+a_3\hat{k}$ and $\vec{b}=b_1\hat{i}+b_2\hat{j}+b_3\hat{k}$ then,

$\theta=\cos^{-1}\left(\dfrac{a_1b_1+a_2b_2+a_3b_3}{\sqrt{a_1^2+a_2^2+a_3^2}\sqrt{b_1^2+b_2^2+b_3^2}}\right)$

This formula is extremely useful for numerical problems and competitive exams like JEE.

Geometrical Interpretation of Scalar (Dot) Product

The geometrical meaning of the dot product is beautifully simple. It is obtained by multiplying the magnitude of one vector with the component (projection) of the other vector in its direction. In other words, the dot product measures how much one vector acts in the direction of another.

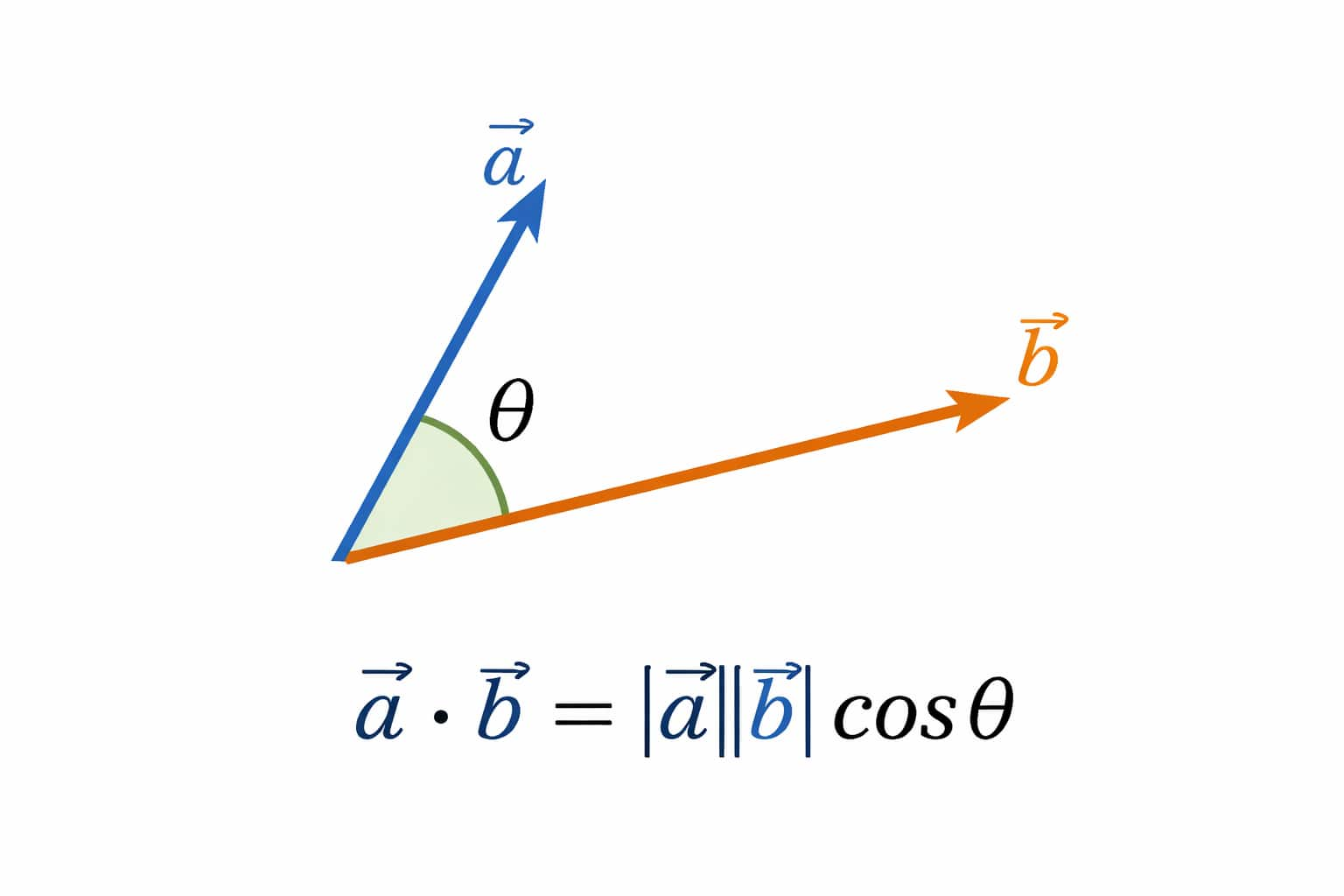
To understand this properly, we must know:

• How to find the magnitude of a vector

• How to find the projection of one vector on another

Magnitude of a Vector

A vector has both direction and magnitude. The magnitude represents the length of the vector and is always a positive quantity. It is calculated by taking the square root of the sum of the squares of its components.

For a vector, $\vec{OP}=x\hat{i}+y\hat{j}+z\hat{k}$ its magnitude is, $|\vec{OP}|=\sqrt{x^2+y^2+z^2}=r$

This formula is the backbone of vector calculations in three-dimensional geometry.

Projection of a Vector on Another Vector

The dot product is mainly used to find the projection of one vector onto another. The projection gives the component of one vector in the direction of the other and is always a scalar quantity.

Let $\vec{a}$ and $\vec{b}$ be two vectors represented by $OA$ and $OB$ respectively, and let $\theta$ be the angle between them.

Draw $BL\perp OA$ and $AM\perp OB$.

From the right-angled triangles formed, we get,

$OL=OB\cos\theta$
$OM=OA\cos\theta$

Here,

• $OL$ is the projection of $\vec{b}$ on $\vec{a}$

• $OM$ is the projection of $\vec{a}$ on $\vec{b}$

So,

• Projection of $\vec{b}$ on $\vec{a}$ is $|\vec{b}|\cos\theta$

• Projection of $\vec{a}$ on $\vec{b}$ is $|\vec{a}|\cos\theta$

This gives a clear geometrical meaning to the dot product and explains why,

$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$

It’s basically “magnitude × projection,” which makes the whole concept feel much more intuitive and less formula-heavy.

Geometrical Meaning of Dot Product in Terms of Projection

From the definition of dot product,

$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$

Now, $\vec{a}\cdot\vec{b}
=|\vec{a}|(|\vec{b}|\cos\theta)
=|\vec{a}|(OB\cos\theta)
=|\vec{a}|(OL)$

This shows that

$\vec{a}\cdot\vec{b}
=(\text{magnitude of }\vec{a})(\text{projection of }\vec{b}\text{ on }\vec{a})$

Again,

$\vec{a}\cdot\vec{b}
=|\vec{b}|(|\vec{a}|\cos\theta)
=|\vec{b}|(OA\cos\theta)
=|\vec{b}|(OM)$

So,

$\vec{a}\cdot\vec{b}
=(\text{magnitude of }\vec{b})(\text{projection of }\vec{a}\text{ on }\vec{b})$

Formula for Projection of One Vector on Another

From the above result,

Projection of $\vec{a}$ on $\vec{b}$ is

$\text{Projection of }\vec{a}\text{ on }\vec{b}
=\dfrac{\vec{a}\cdot\vec{b}}{|\vec{b}|}
=\vec{a}\cdot\dfrac{\vec{b}}{|\vec{b}|}
=\vec{a}\cdot\hat{b}$

Similarly,

Projection of $\vec{b}$ on $\vec{a}$ is

$\text{Projection of }\vec{b}\text{ on }\vec{a}
=\dfrac{\vec{a}\cdot\vec{b}}{|\vec{a}|}
=\vec{b}\cdot\dfrac{\vec{a}}{|\vec{a}|}
=\vec{b}\cdot\hat{a}$

where $\hat{a}$ and $\hat{b}$ are unit vectors in the directions of $\vec{a}$ and $\vec{b}$ respectively.

These formulas are super important for numerical problems and appear very frequently in exams.

Working Rule to Find the Dot Product of Two Vectors

When vectors are expressed in terms of unit vectors $\hat{i},\hat{j},\hat{k}$ along the x, y, and z axes, the dot product is calculated component-wise.

If $\vec{a}=a_1\hat{i}+a_2\hat{j}+a_3\hat{k}$ and $\vec{b}=b_1\hat{i}+b_2\hat{j}+b_3\hat{k}$ then, $\vec{a}\cdot\vec{b}
=(a_1\hat{i}+a_2\hat{j}+a_3\hat{k})\cdot(b_1\hat{i}+b_2\hat{j}+b_3\hat{k})$

$=a_1b_1(\hat{i}\cdot\hat{i})
+a_1b_2(\hat{i}\cdot\hat{j})
+a_1b_3(\hat{i}\cdot\hat{k})
+a_2b_1(\hat{j}\cdot\hat{i})
+a_2b_2(\hat{j}\cdot\hat{j})
+a_2b_3(\hat{j}\cdot\hat{k})$

$+a_3b_1(\hat{k}\cdot\hat{i})
+a_3b_2(\hat{k}\cdot\hat{j})
+a_3b_3(\hat{k}\cdot\hat{k})$

Since

$\hat{i}\cdot\hat{i}=1,;\hat{j}\cdot\hat{j}=1,;\hat{k}\cdot\hat{k}=1$
and

$\hat{i}\cdot\hat{j}=\hat{j}\cdot\hat{k}=\hat{k}\cdot\hat{i}=0$,

we get,

$\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2+a_3b_3$

This is the fastest and most practical rule to compute the dot product in coordinate geometry.

Dot Product and Perpendicularity of Vectors

For any two non-zero vectors $\vec{a}$ and $\vec{b}$,

$\vec{a}\cdot\vec{b}=0 \Leftrightarrow \vec{a}\perp\vec{b}$

So, if the dot product is zero, the vectors are perpendicular.
If the vectors are perpendicular, their dot product must be zero.

This is one of the most powerful tests for orthogonality.

Dot Product of Unit Vectors

Since $\hat{i},\hat{j},\hat{k}$ are mutually perpendicular unit vectors,

$\hat{i}\cdot\hat{j}=\hat{j}\cdot\hat{i}=0$
$\hat{j}\cdot\hat{k}=\hat{k}\cdot\hat{j}=0$
$\hat{k}\cdot\hat{i}=\hat{i}\cdot\hat{k}=0$

Also, because they are unit vectors,

$\hat{i}\cdot\hat{i}=|\hat{i}|^2=1$
$\hat{j}\cdot\hat{j}=|\hat{j}|^2=1$
$\hat{k}\cdot\hat{k}=|\hat{k}|^2=1$

Special Case: Dot Product of a Vector with Itself

If $\theta=0$, then

$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|$

In particular,

$\vec{a}\cdot\vec{a}=|\vec{a}|^2$

This result is used directly to find the magnitude of a vector:

$|\vec{a}|=\sqrt{\vec{a}\cdot\vec{a}}$

Simple, powerful, and extremely useful. Dot product really is the Swiss army knife of vector algebra.

Solved Examples on Dot (Scalar) Product of Two Vectors

Example 1: Let $S$ be the set of all $a \in \mathbb{R}$ for which the angle between the vectors $\vec{u}=a(\log_e b)\hat{i}-6\hat{j}+3\hat{k}$ and $\vec{v}=(\log_e b)\hat{i}+2\hat{j}+2a(\log_e b)\hat{k}$, where $b>1$, is acute. Find the set $S$.

Solution

For the angle between two vectors to be acute, their dot product must be positive:

$\vec{u}\cdot\vec{v}>0$

Now, $\vec{u}\cdot\vec{v} =[a(\log b)\hat{i}-6\hat{j}+3\hat{k}]\cdot[(\log b)\hat{i}+2\hat{j}+2a(\log b)\hat{k}]$

$=a(\log b)^2-12+6a(\log b)$

So, $a(\log b)^2+6a(\log b)-12>0$

Since $b>1$, we have $\log b>0$.
Let $\log b=t$, so $t>0$.

Then, $at^2+6at-12>0$ for all $t>0$

But at $t=0$,

$f(t)=at^2+6at-12=-12<0$

Hence, the expression cannot be positive for all $t>0$ for any value of $a$. Therefore, no real value of $a$ satisfies the condition.

So, $S=\varnothing$

Hence, the answer is $\Phi$.

Example 2: Let a vector $\vec{a}$ have magnitude $9$. Let a vector $\vec{b}$ be such that for every $(x,y)\in\mathbb{R}^2-{(0,0)}$, the vector $(x\vec{a}+y\vec{b})$ is perpendicular to $(6y\vec{a}-18x\vec{b})$. Find $|\vec{a}\times\vec{b}|$. [JEE Main 2022]

Solution

Given, $|\vec{a}|=9$

Since the vectors are perpendicular,

$(x\vec{a}+y\vec{b})\cdot(6y\vec{a}-18x\vec{b})=0$

Expand: $=6xy(\vec{a}\cdot\vec{a})-18x^2(\vec{a}\cdot\vec{b})+6y^2(\vec{a}\cdot\vec{b})-18xy(\vec{b}\cdot\vec{b})=0$

$=6xy(|\vec{a}|^2-3|\vec{b}|^2)+(\vec{a}\cdot\vec{b})(y^2-3x^2)=0$

This must hold for all $x$ and $y$.
Hence, the coefficients of both independent terms must be zero:

$|\vec{a}|^2=3|\vec{b}|^2$ and $\vec{a}\cdot\vec{b}=0$

From $|\vec{a}|=9$,

$81=3|\vec{b}|^2$
$\Rightarrow |\vec{b}|^2=27$

Now, $|\vec{a}\times\vec{b}|^2
=|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2$

$=81\times27-0$

$=2187$

So, $|\vec{a}\times\vec{b}|=\sqrt{2187}$
$=27\sqrt{3}$

Hence, the answer is: $\boxed{27\sqrt{3}}$

Example 3: In a triangle ABC , if $|\overrightarrow{\mathrm{BC}}|=3,|\overrightarrow{\mathrm{CA}}|=5$ and $|\overrightarrow{\mathrm{BA}}|=7$, then the projection of the vector $\overrightarrow{\mathrm{BA}}$ on $\overrightarrow{\mathrm{BC}}$ is equal to [JEE MAINS 2021]

Solution

Clearly, the projection of $\overrightarrow{AB}$ on $\overrightarrow{BC}$ is

$|\overrightarrow{AB}|\cos B = 7\cos B$

To find $\cos B$, we apply the Cosine Rule in the triangle:

$\cos B=\dfrac{a^2+c^2-b^2}{2ac}$

Substitute the given values:

$\cos B=\dfrac{9+49-25}{2(3)(7)}$

$=\dfrac{33}{42}$

$=\dfrac{11}{14}$

Now, the projection becomes:

$\text{Projection}
=7\cos B
=7\times\dfrac{11}{14}
=\dfrac{11}{2}$

Hence, the correct option is $\dfrac{11}{2}$

List of Topics Related to Vector Algebra

This section brings together all essential NCERT resources, including well-structured notes, step-by-step solutions, and exemplar problems, perfectly aligned with the current syllabus. It is designed to build strong conceptual clarity and help you master every aspect of the dot product of two vectors with confidence.

Types of Vectors - Introduction and Solved Examples

Definition, Vector Addition and Subtraction, Differences ...

Addition of Vectors and Subtraction of Vectors

Multiplication Of Vectors by a Scalar Quantity

Components Of A Vector Along And Perpendicular To Another Vector

NCERT Resources

This section provides a complete collection of NCERT-based resources including detailed notes, solved examples, and exemplar solutions, all strictly aligned with the latest syllabus. These materials are designed to strengthen your fundamentals and ensure clear understanding of every concept related to the dot product of vectors.

NCERT Maths Class 12th Notes for Chapter 10 - Vector Algebra

NCERT Maths Class 12th Solutions for Chapter 10 - Vector Algebra

NCERT Maths Class 12th Exemplar Solutions for Chapter 10 - Vector Algebra

Practice Questions based on Dot Product of two vectors

This section contains carefully selected practice questions based on the dot product of two vectors to help you strengthen your conceptual understanding and problem-solving skills. The questions range from basic applications to exam-level problems involving angles, projections, and perpendicularity. Regular practice from this section will make you faster, more confident, and more accurate in vector algebra.

Dot Product Of Two Vectors- Practice Question MCQ

We have provided below the practice questions based on the topics related to dot product of two vectors: